



Simulación de salto de partículas de polvo generado por acción del viento utilizando Comsol Multiphysics®
Simulation of dust particles saltation generated by the action of the wind using Comsol Multiphysics®
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
Recepción: 22 Noviembre 2016
Aprobación: 30 Enero 2017
Resumen: Este trabajo presenta un modelo de salto de partículas en tres dimensiones generado mediante dinámica de fluidos computacional (CFD) cuya aplicación puede extenderse en cualquier lugar geográfico y actividad que involucre una exposición directa de partículas hacia la atmósfera por acción del viento. El fenómeno de salto de partículas involucra la interacción de diversos procesos como: el movimiento de la partícula en el salto, las modificaciones del perfil de viento a través de la transferencia de momento entre el flujo de viento y las partículas en salto, y la colisión de partículas con el suelo que ocasionará la posterior salpicadura de partículas de la superficie en la corriente del fluido. Este modelo de dispersión describe el comportamiento del viento generado por distintas velocidades en dirección horizontal y el perfil formado por diferentes rugosidades del terreno. Además, incluye la trayectoria de movimiento de partículas debido a la fuerza de cizalladura del aire, gravedad, arrastre y efectos de turbulencia.
Palabras clave: Salto (saltación) de Partículas, Perfil de Viento, Modelo de Dispersión, CFD.
Abstract: This paper presents a three-dimensional model of dust particles saltation generated through computational fluid dynamics (CFD) that could be applied in any geographical location and any activity that involves direct exposure of particles into the atmosphere by wind. The phenomenon of particle saltation is a consequence of the interaction of several processes like the motion of the particle during the jump, changes in the wind profile through momentum transfer between wind flow and the saltating particles, and particle collision with the ground that causes the splash of surface particles in the fluid stream. This dispersion model describes the behavior of wind generated at different speeds in the horizontal direction and the wind profiles at different terrain roughness. This model includes the motion of particles due to shear force, gravity, drag and the effect of turbulence.
Keywords: Saltating Particles, Wind Profile, Dispersion Model, CFD.
INTRODUCCIÓN
El polvo arrastrado por el viento es uno de los factores responsables de la suspensión de partículas finas en la atmósfera, la creación de dunas de arena y la erosión característica de actividades geológicas. Por ejemplo, varios países como España, Reino Unido, Portugal, Cuba y otros países de la zona del Caribe se han visto afectadas por nubes de polvo provenientes del desierto africano del Sahara [1]. Estas tormentas de polvo, según su tamaño pueden permanecer suspendidas desde días hasta semanas. Estas partículas pueden ser toxicas lo que puede provocar diversos efectos negativos sobre el medio ambiente y salud ya que podrían contribuir a la superación de los niveles de contaminación permitidos [2].
El material finamente particulado es conocido comúnmente como polvo y se presenta en tamaños que varían entre 1-1000 µm y su composición química varía en función de las características del material del cual se desprende [3]. El polvo causa serias molestias a las personas que se encuentran expuestas directamente y a las comunidades que se hallan dentro del área de influencia de operación, al disminuir la calidad del aire respirable [4]. Pequeñas partículas en suspensión en el aire son contaminantes relevantes para el ser humano. El viento puede transportar partículas ultra finas (es decir, aquellas partículas con diámetros menores a 1 mm), como metales y metaloides, que al ser aspiradas por personas y animales pasan por la tráquea y finalmente llegarán a los pulmones [5].
El fenómeno de salto (o saltación) inicia cuando la velocidad del viento aumenta y genera que las partículas de polvo entre 70-500 mm de diámetro sean las primeras en moverse [6]. Dependiendo de su volumen tienden a seguir diferente trayectoria: generalmente, partículas de 500 mm de diámetro solamente ruedan o se deslizan; partículas intermedias son levantadas y rebotan en una serie de saltos a lo largo de toda la superficie; y, partículas menores a 70 mm no son levantadas ya que sus fuerzas de atracción son mayores que la fuerza de cizalladura del viento [7]. Cuando las partículas en salto impactan contra el suelo pueden movilizar una amplia gama de partículas con diferentes tamaños; esto se da ya que al momento de impactar en el terreno parte del momento horizontal, ganado por acción del viento, es parcialmente convertido en momento vertical [7]. Durante el fenómeno de salto, el perfil de viento que se forma es clave ya que determinará la cantidad de momento que será transferida a dicha partícula en salto.
El viento es un fluido que si se mueve en dirección paralela a una superficie sufre un rozamiento continuo en la zona de contacto, este contacto produce una fuerza de cizallamiento por lo que el perfil de viento mantendrá una forma logarítmica [7]. En la Figura 1 se puede visualizar una representación esquemática para el fenómeno de salto de partículas y un perfil logarítmico de viento, . Por otro lado, el objetivo de este manuscrito es generar un modelo general que elucide el salto de partículas de polvo generado por corrientes de aire.
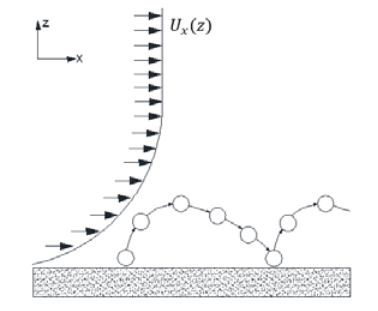
Representación esquemática de salto de partículas y perfil de viento.
MÉTODOS Y MATERIALES
Descripción del modelo
El modelo simula la interacción de tres procesos: el comportamiento del viento, la trayectoria de las partículas en salto y la transferencia de momento entre el flujo de viento y las partículas suspendidas. Es un modelo en tres dimensiones que incluye flujo turbulento k-e, fuerza arrastre, gravedad e interacciones entre partículas y fluido. El modelo rechaza la colisión entre partículas, las fuerzas electrostáticas y el giro de partículas sobre su propio eje (Fuerza de Magnus) ya que se busca realizar un modelo simplificado, que demuestre un comportamiento idealizado de saltación. Sin embargo, se podría incorporar este tipo de fuerzas incluyendo una física que gobierne estos efectos. El modelo turbulento utilizado es una adaptación del modelo estándar de k-e tomando en cuenta constantes sugeridas por Richard & Hoxey [8].
Software
COMSOL MULTIPHYSICS 5.1® es utilizado para la creación de geometrías, generación de mallas, simulación el flujo turbulento de aire y el salto de partículas. Las simulaciones se realizaron en un sistema operativo Windows con procesador Intel® Core™ i5-4200U CPU @ 160 GHz.
Geometría y mallado
El dominio de estudio es una caja que se extiende 2 m en el eje X, 0.5 m en Y y 0.5 m en Z como se muestra en la Figura 2. Adicionalmente, se generaron 10 capas de 0.01 m de alto desde la base de la caja con el fin de obtener una mejor aproximación de flujo turbulento y del fenómeno de salto cerca del terreno (base) de la caja. La geometría utiliza un tipo de mallado de tetraedros libres (free tetrahedral) como se muestra en la Figura 3. En las capas superiores se estableció una malla normal (normal) y fina (fine), como se muestra en la Figura 3a y 3b, respectivamente. En las 5 capas inferiores se estableció una malla extra fina (extra fine) por ser una zona crítica donde se genera la mayor cantidad de saltos (Figura 3c). Comsol es un programa iterativo que según el mallado genera diversos elementos para mejorar la solución final. Este tipo de mallado generó un total de 680 495 elementos en todo el dominio.
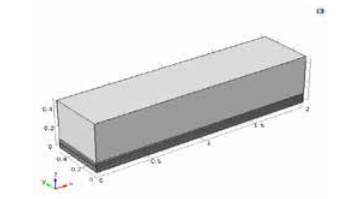
Geometría del dominio de estudio. La caja se extiende 2 m en X, 0.5 m en Y y 0.5 m en Z.
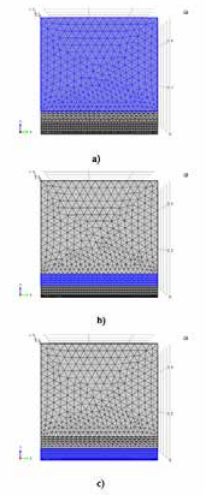
a) Malla normal (Normal mesh), b) Malla fina (Fine mesh), c) Malla extra fina (Extra fine mesh).
Perfil de viento
El perfil de viento es clave en el salto de partículas pues regula la cantidad de momento que se transfiere a la partícula en salto. La ecuación de perfil de viento adoptada para las simulaciones es logarítmica y en estado estacionario representada por la ecuación 1 [9-10].
 (1)
(1)Donde z [m] es la distancia vertical desde la base, u* [m/s] es la velocidad de cizalladura del viento, k es la constante de Von Karman y zo [m] es la rugosidad de la superficie. La velocidad de cizalladura del viento puede ser calculada según la ecuación 2 [9-10].
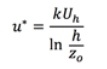 (2)
(2) Donde Uh(m/s) es la velocidad de referencia a la altura de h [m].
Para el desarrollo del modelo en Comsol se utilizó el módulo de transporte de fluidos con la física de Turbulent Flow, k.e (spf). Este es un modelo de dos ecuaciones que sirve para simular las características de un fluido turbulento. La primera variable de transporte, k, determina la energía cinética turbulenta y la segunda variable, e, determina la disipación de energía turbulenta. Ambas variables están determinadas por las ecuaciones 3 y 4 [8].
 (3)
(3)Donde Cu es una constante del modelo igual a 0.013 [8].
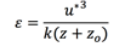 (4)
(4)Para la simulación de partículas en salto se utiliza una velocidad de cizalladura del viento de 0.0441 m/s. Esta velocidad, a una altura de 10 m, es equivalente a 1 m/s y según la escala de Beautfort se describe como una ventolina en la cual el humo indica la dirección del viento [11]. Se utiliza la constante de Von Karman con un valor de 0.42 y un valor de de 7.31x10-4 m que representa un valor equivalente a la rugosidad aerodinámica típica deun desierto [7].
Para la generación del perfil de viento se realizó un estudio en estado estacionario donde se definió una cara de ingreso (inlet) con la condición de velocidad en el eje X equivalente a la ecuación 2; una cara de salida (pressure oulet), con una condición de borde de presión igual a 1 atm; la cara superior se estableció una cara de frontera abierta donde no exista estrés viscoso; y, en las caras laterales se impuso una función de simetría, la cual describe que lo que sucede al interior de las paredes laterales sucede a su exterior. Dentro de los ajustes de terreno se utiliza una función de pared (wall functions), en la cual se aplica una rugosidad equivalente, , y este valor se calcula con la ecuación 5 [12].
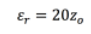 (5)
(5)Trayectoria de partículas
El movimiento de las partículas en salto está determinado principalmente por la fuerza gravitacional y las fuerzas proporcionadas por el fluido propiamente. La principal fuerza que ejerce el fluido y afecta la trayectoria es la fuerza de arrastre (drag force), Fd. Esta fuerza está determinada por las ecuaciones 6, 7 y 8 [13].
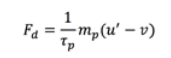 (6)
(6)
 (7)
(7)
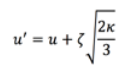 (8)
(8)Donde τp [s] es el tiempo de respuesta de la velocidad de partícula, mp[kg] es la masa, v [m/s]es la velocidad de las partículas, es la viscosidad dinámica del fluido [Pa·s], ρp [kg/m3] es la densidad de la partícula, dp [m] diámetro de la partícula y u’ [m/s] es la velocidad del fluido. Al utilizar un flujo con disipación turbulenta, el campo de velocidad del fluido se adapta a la ecuación 8.
Esta ecuación consta de dos términos: primero u [m/s] representa la velocidad media del fluido y el segundo término representa una fluctuación turbulenta donde k [m2/s2] es la energía cinética turbulenta y ζ es un número aleatorio distribuido normalmente con media de cero y desviación estándar de uno generado por el programa. Estas ecuaciones son adaptaciones de la ley de arrastre establecida por George Gabriel Stokes con el modelo de flujos cargados de partículas. Este modelo se refiere a una clase de flujo de fluido de dos fases en el que una de las fases está conectada de forma continua (fase continua o vehículo) y la otra fase se compone de partículas pequeñas inmiscibles (fase dispersa o de partículas) [14].
Las partículas saltantes al encontrarse en el sistema gravitatorio terrestre “sienten” la fuerza de gravedad Fg determinada por la ecuación 9 [13].
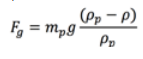 (9)
(9)Donde g [m/s2] es la aceleración de la gravedad y ρ [kg/m3] es la densidad del aire.
Para determinar las trayectorias se realizó un estudio dependiente del tiempo en intervalos de 0.01-0.001 s, dependiendo del estudio a realizarse. Por ejemplo, para obtener una mejorvisualización de los saltos realizados a lo largo de la superficie, se debe asignar un menor intervalo de tiempo para poder captar el momento exacto en que la partícula topa el suelo. En las propiedades de las partículas se fijó una densidad promedio de polvo igual a 2.5 g/cm3 y se realizó el estudio para diámetros de partículas de 100, 250 y 500 mm. Se ingresaron 20 partículas dispersas por toda la cara frontal a diferentes alturas que serán arrastradas de acuerdo a las ecuaciones que representan la trayectoria de partículas y el perfil de viento. En el terreno se mantiene la rugosidad establecida por el perfil de viento y se adiciona una opción de rebote. Las condiciones para la fuerza de arrastre como el campo de velocidad y la viscosidad dinámica van a depender del estudio estacionario de perfil de viento.
RESULTADOS Y DISCUSIONES
Para ambos estudios se utilizó el solucionador de Comsol GMRS (generador de residuo mínimo) con un método segregado de dos etapas con una tolerancia de 1×10-4. Se realizó un estudio de tolerancias en la malla para valores de 1×10-3 a 1×10-4 y 1×10-4 a 1×10-5 de los cuales se encontró errores menores al 10% y 5% respectivamente. El solucionador GMRS es un método iterativo, en el cual se requiere que se especifique el número de iteraciones que el solucionador llevará a cabo hasta que se reinicie (el valor predeterminado es 50).
Perfil de viento
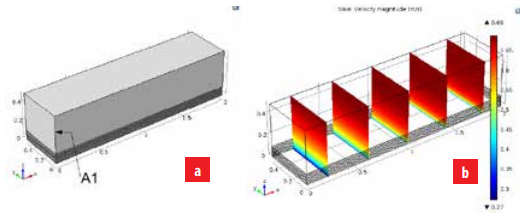
a) Corte de velocidades en el dominio de estudio. b) Corte A1 para determinación del perfil de viento.
En la Figura 4a) se presentan varios cortes a lo largo del dominio de estudio, donde se puede percibir que en la zona de contacto se da la mayor cantidad de cizallamiento con el fluido. Para poder apreciar el perfil y determinar cómo varía la velocidad de viento según la altura y comprobar el comportamiento del mismo dentro del dominio de estudio se realizó un corte vertical (A1) como se muestra en la Figura 4b).
La Figura 5 equivalente al corte A1, presenta la variación de la magnitud del viento en función de la altura. Se tiene un perfil de viento logarítmico el cual aparentemente sigue creciendo. El perfil no llega a estabilizarse a una velocidad constante ya que la altura del modelo fue truncado a una altura de 0.5 m. Generalmente, los valores de velocidad referenciales se toman a 10 m de altura pues la velocidad a esta altura ya tiene unatendencia estable [14]. A 10 m, la velocidad equivalente sería de 1 m/s.
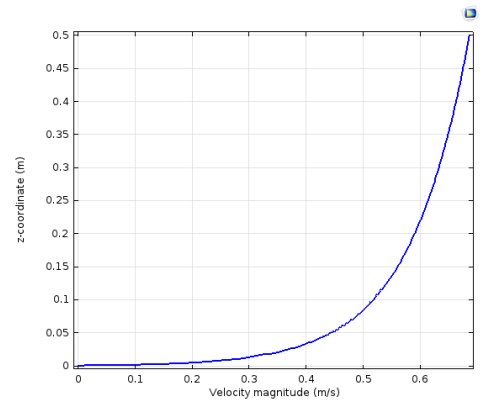
Perfil de velocidad en el corte A1.
Trayectoria de partículas
Para el estudio de salto de partículas se arrojaron 20 partículas a diferentes alturas sin velocidad inicial, esto quiere decir que ganarán momento netamente del perfil de viento descrito previamente en los métodos y materiales. En la Figura 6a) se aprecia una representación de las 20 partículas en su posición inicial en la cara frontal. Las partículas están coloreadas en función a la velocidad que el viento transferirá de acuerdo a la altura.
Ya que el terreno es casi ideal, no hay geometrías que obstaculicen la trayectoria y la velocidad del viento ingresa linealmente a lo largo del eje X. Las partículas de estudio casi no“sentirán” desviaciones en el eje Y. No obstante, este modelo puede ser aplicado en dominios que sí incluyan efectos de obstrucciones y topográficos.
En la Figura 6b-d se observa la posición de las partículas después de 3 s, en este punto se nota que todas las partículas están casi a nivel del suelo y con la mayor parte de su energía disipada.
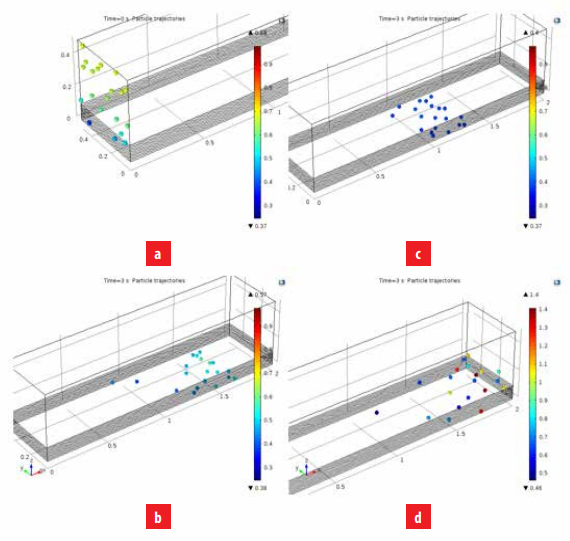
a) Posición inicial de partículas, b) Posición después de 3 (s), partículas de 100 mm de diámetro, c) Posición después de 3 (s), partículas de 250 mm de diámetro, d) Posición después de 3 (s), :partículas de 500 mm de diámetro.
En la Figura 7a) se representan partículas con diferentes diámetros que son lanzadas a la misma altura en el eje Y igual a 0.49 m. Se puede apreciar que la energía de rebote de las partículas es directamente proporcional a su diámetro ya que partículas del 100 μm tienden a caer y perder casi toda su energía inmediatamente. Por otro lado, partículas de 500 μm de diámetro tienden a generar la mayor cantidad de saltos.
En la Figura 7b) se observa las trayectorias y comportamiento de partículas 500 μm de diámetro soltadas desde diferentes alturas. Las partículas que fueron expulsadas desde una altura mayor tienden a generar una mayor serie de saltos.
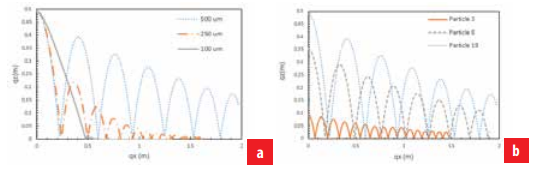
a) Trayectoria de partículas lanzadas a 0.49 m en el eje Y. b) Trayectoria de partículas de 500 mm de diámetro lanzadas a diferentes alturas en el eje Y.
Comparación
El modelo propuesto se simuló tomando las condiciones y ajustes de contornos, tanto para el perfil de viento como para el salto de partículas, establecidas por Jasper F. Kok y Nilton O. Renno descritas en el modelo COMSALT [7]. El mencionado estudio utilizó una velocidad de cizallamiento igual a 0.4 m/s y una rugosidad equivalente representada por la ecuación 10 [7,10,15].
Además, las partículas fueron expulsadas desde la superficie con una rapidez inicial de 1 m/s y un ángulo de 40o desde la horizontal. Los datos obtenidos y la comparación con respecto al modelo COMSALT se representan en la Figura 8.
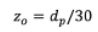 (10)
(10)Las trayectorias obtenidas en el modelo descrito en este trabajo de investigación muestran un comportamiento semejante a las trayectorias obtenidas en el modelo COMSALT [7] que fueron validadas por una serie de datos experimentales. Las partículas más pequeñas descritas en la Figura 8a) tienden a viajar distancias mayores en el eje horizontal. Por otro lado, las partículas de mayor tamaño (Figure 8b) ganan más momento vertical, pero al tener una mayor masa son mayormente afectadas por la fuerza de gravedad por lo que tienden a caer más rápido.
Como se mencionó anteriormente, las partículas con mayor diámetro son las causantes que partículas menores entren en salto. En la Figura 7a) se muestra cómo estas partículas generan la mayor cantidad de saltos a lo largo de una superficie, ya que, al obtener una mayor cantidad de momento vertical, generan una mayor energía potencial lo que conlleva a que puedan realizar una mayor cantidad de saltos a lo largo de la superficie en comparación a partículas con menor masa. Además, se realizó un análisis de conservación de energías en diferentes puntos para cuantificar la energía perdida en cada rebote. La ecuación para determinar la energía perdida está dada por la ecuación 11[16].
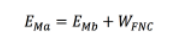 (11)
(11)Donde EMa y EMb es la energía mecánica en el punto a y b respectivamente, los puntos a y b son elegidos aleatoriamente entre cada rebote que realiza la partícula, y WFNC es el trabajo de las fuerzas no conservativas que en este caso será la energía perdida por fricción en cada contacto de la partícula con la superficie. La energía mecánica está representada por la suma entre la energía cinética (Ek), ecuación 12, y potencial (Ep),ecuación 13, en cada punto respectivamente [16].
 (12)
(12)
 (13)
(13)Donde v es la velocidad de la partícula y h la altura en la que se encuentra la partícula en un momento determinado.
Se realizó este estudio de conservación de energía tomando en cuenta el antes y después de cada salto para la partícula 19, representada en la Figura 7b), ya que es la que más energía potencial tiene y da la mayor cantidad de saltos a lo largo de la superficie. En cada salto realizado por la partícula hay una pérdida promedio del 15± 5% en cada salto.
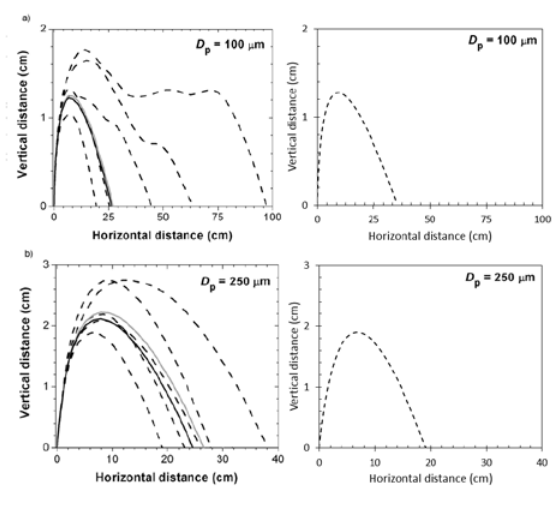
Comparación de trayectorias de partículas con diámetros de (a) 100 μm, (b) 250 μm. En el lado derecho se presentan trayectorias obtenidas con el modelo de Comsol y en el lado izquierdo los resultados por COMSALT. Las figuras se han reproducido con los permisos de autor Kok & Renno (2009) [4].
Aplicación del modelo sobre un dominio irregular
Con el fin de mostrar las bondades del modelo, en la Figura 9 se muestra un dominio con terreno irregular y con cortes de velocidad del viento y la trayectoria de una partícula de 500 μm de diámetro. Como es evidente, la topografía juega un papel importante en el salto de las partículas desviándolas de su comportamiento ideal, es decir, cuando el terreno es plano.
En la Figura 9b) se nota claramente que el viento pierde su tendencia logarítmica. En las zonas con mayor irregularidad existe una aceleración del fluido para poder superar el obstáculo generado por el propio terreno. Esto causa que las partículas que pasen por estas zonas, experimenten una mayor aceleración, lo cual causara desviaciones en la trayectoria de estas. Por otro lado, en la Figura 9c) muestra la trayectoria de una partícula de 500 μm de diámetro. Esta partícula es transportada a lo largo de la superficie por una serie de saltos, con movimientos hacia adelante y hacia atrás. Este tipo de movimiento ocurre por la irregularidad del terreno, el tipo de salto va a depender directamente del ángulo de impacto sobre la superficie inclinada [17].

(a) Geometría con terreno irregular, (b) corte de velocidades, (c) trayectoria de partícula de 500 μm de diámetro.
Se ha realizado un modelo dinámico en tres dimensiones que incluye las ecuaciones y los parámetros más relevantes para el estudio de salto de partículas por acción del viento debido a las fuerzas gravitacionales y de arrastre. El modelo desarrollado es general e incluye una porción de terreno muy pequeña con características casi ideales. Al ser un modelo generalizado con la posibilidad de realizar adaptaciones a problemas similares con condiciones físicas distintas; el modelo puede ser llevado a la realización de proyectos futuros, en el cual se puede incluir efectos de topografía, análisis bajo diferentes velocidades y direcciones de viento y caracterización de la composición del suelo para describir un modelo de dispersión reales que puede ser aplicado en cualquier lugar geográfico y cualquier actividad que involucre una exposición de material particulado hacia la atmósfera. Este tipo de estudios es importante ya que se puede predecir el impacto ambiental que se podría generar durante ciertas actividades. Por ejemplo, en el Ecuador no se cuenta con información precisa del estado de la calidad del aire en término de material particulado en función de tamaño, y la gestión en este ámbito es de origen creciente [18]. Canteras y minas a cielo abierto han sido identificados como fuentes considerables de material particulado (PM2.5 y PM10) según el estudio de “Plan Nacional de la Calidad del Aire” [19].
Adicionalmente, existe falta de información precisa sobre la ubicación de actividades mineras, la operación y tipos de equipos utilizados. Esto hace que sea difícil determinar su impacto en las zonas aledañas y sobre todo en zonas pobladas. Los principales riesgos en la industria de la minería incluyen la exposición a partículas en el aire que va a depender de los parámetros de las minas y canteras (por ejemplo, profundidad), la composición del mineral y la roca circundante, y los métodos de explotación [20]. Se ha encontrado que el promedio anual de PM2.5 (65 µg/m3) para el período 2005 hasta agosto del 2007 es prácticamente constantes en todas las estaciones y rebasa el límite máximo permisible de 15 µg/m3 establecido en la Norma Ecuatoriana de Calidad del Aire siendo, además, el valor referencial recomendado por la OMS de 10 µg/m3 [21].
AGRADECIMIENTOS
Esta investigación fue financiada mediante el Chancellor Grant 2015 de la Universidad San Francisco de Quito-USFQ. Los autores agradecen además al Departamento de Ingeniería Química y al Colegio de Ciencias e Ingenierías por apoyar las iniciativas que involucran simulaciones asistidas por computadora.
CONTRIBUCIÓN DE LOS AUTORES
El proyecto fue concebido por Andrea Landázuri. Los fondos y recursos computacionales fueron adquiridos y administrados por Andrea Landázuri. Vladimir Benavides ejecutó las simulaciones CFD y de partículas, generó las figuras y tablas, y redactó el manuscrito preliminar bajo la dirección de Andrea Landázuri. En conjunto, revisaron y editaron el artículo final.
REFERENCIAS
[1] Fernández, A. (2014). Nubes de polvo del Sahara: cómo nos afectan. Retrieved from http://www.consumer.es/web/es/medio_ambiente/naturaleza/2014/05/08/219856.php
[2] Echarri, L. (2007). Tema 7 Contaminación de la atmósfera. Pamplona.
[3] García, H. (1998). Guía Ambiental para Minería de Carbón a Cielo Abierto (MCCA). Retrieved from http://www.upme.gov.co/guia_ambiental/carbon/gestion/guias/min_cab/contenid/medidas2.htm
[4] Guía Minero Ambiental de, & Explotación. (2001). Manejo de Impactos Ambientales. Santiago de Chile.
[5] CCSSO. (2002). ¿Cuáles son los Efectos del Polvo en los Pulmones ? Retrieved from http://www.ccsso.ca/oshanswers/chemicals/lungs_dust.html
[6] Kok, J. F., Parteli, E. J. R., Michaels, T. I., & Karam, D. B. (2012). The physics of wind-blown sand and dust. Reports on Progress in Physics, 75(10), 106901. https://doi.org/10.1088/0034-4885/75/10/106901
[7] Kok, J. F., & Renno, N. O. (2009). A comprehensive numerical model of steady state saltation (COMSALT). Journal of Geophysical Research Atmospheres, 114(17). https://doi.org/10.1029/2009JD011702
[8] Richards, P. J., & Hoxey, R. P. (1993). Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. Journal of Wind Engineering and Industrial Aerodynamics, 46–47(0), 145–153. https:// doi.org/http://dx.doi.org/10.1016/0167-6105(93)90124-7
[9] Seinfeld,J. H., & Pandis, S. N. (2006). Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. Atmospheric Chemistry and Physics (Vol. 2nd). Retrieved from http://www.knovel.com/knovel2/Toc.jsp?BookID=2126
[10] Bagnold, R. A. (1941). The Physics of Blown Sand and Desert Dunes. Nature, 148, 480–481. https://doi.org/10.1038/148480a0
[11] SPC. (2016). Beaufort Wind Scale. Retrieved from http://www.spc.noaa.gov/faq/tornado/beaufort.html
[12] USEPA. (2000). Meteorological Monitoring Guidance for Regulatory Modeling Applications. Epa-454/R-99-005, 171. Retrieved from http://www.epa.gov/scram001/guidance/met/mmgrma.pdf
[13] COMSOL. (2015). CFD Module User’s Guide.
[14] Maxey M. R., R. J. J. (1983). Equation of motion for a small rigid sphere in a nonuniform flow. In Phys. Fluids (pp.883–889).
[15] Greeley, R., & Iversen, J. (1987). Wind as a Geological Process On Earth, Mars, Venus and Titan. Cambridge: Cambridge Planetary Science Old.
[16] Giancoli, D. C. (2004). Physics: Principles with Applications. ReCALL (Vol. 1). https://doi.org/10.1017/CBO9781107415324.004
[17] Kobayakawa, M., Fujimoto, A., Sakata, M., Yasuda, M., & Matsusaka, S. (2014). Numerical and theoretical study of particle saltation on an obliquely oscillating plate. Advanced Powder Technology, 25(6), 1854–1859. https://doi.org/10.1016/j.apt.2014.07.017
[18] GeoEcuador. (2008). Informe sobre el estado. Retrieved from http://www.flacsoandes.edu.ec/libros/digital/41444.pdf
[19] Ambiente, M. del. (2010). Plan Nacional de la Calidad del Aire. Retrieved from http://www.ambiente.gob.ec/wp-content/uploads/downloads/2012/10/libro-calidad-aire-1-final.pdf
[20] Tarras-Wahlberg, H., Flachier, A., Fredriksson, G., Lane, S., Lundberg, B., & Sangfors, O. (2000). BioOne sees sustainable scholarly publishing as an inherently collaborative enterprise connecting authors, nonprofit publishers, academic institutions, research libraries, and research funders in the common goal of maximizing access to critical research. Royal Swedish Academy of Sciences.
[21] CORPAIRE. (2005). Plan de Manejo de la Calidad del Aire del Distrito Metropolitano de Quito. Periodo 2005-2010. Retrieved from http://webcache.googleusercontent.com/search?q=cache:fAtuJTWznFQJ:www.quitoambiente.gob.ec/ambiente/index.php/biblioteca-digital/category/61-politicas-y-planeacion-ambiental%3Fdownload%3D529:calidad-del-aire-final+&cd=1&hl=es&ct=clnk&client=firefox-b-ab