SECCIÓN C: INGENIERÍAS
Muros de entramado ligero de madera: una revisión del estado del arte
Muros de entramado ligero de madera: una revisión del estado del arte
Avances en Ciencias e Ingenierías, vol. 16, núm. 1, e3270, 2024
Universidad San Francisco de Quito
Recepción: 20 Febrero 2024
Aprobación: 07 Marzo 2024
Resumen: Tras el sismo de Northridge en 1994, mismo que ocasionó daños significativos a las estructuras de madera, la investigación sobre la respuesta sísmica de muros de entramado ligero ha experimentado un notable crecimiento. Este interés se ha extendido más allá de la zona afectada. Autores de países con tradición constructiva en madera han experimentado sobre la geometría de los componentes del muro, la conexión entre el marco y el panel de revestimiento y la implementación de nuevos materiales. En complemento a la parte experimental se han desarrollado modelos numéricos que capturan de forma precisa el comportamiento ante carga sísmica. Este artículo de revisión del estado del arte tiene como objetivo sintetizar las innovaciones y hallazgos encontrados durante la última década, mismos que se detallan en artículos de investigación disponibles en la base de datos ScienceDirect, haciendo de este trabajo una referencia inicial para explorar futuras líneas de investigación en países donde este sistema no ha sido mayormente divulgado. Se ha adoptado la metodología indicada en la declaración PRISMA para dar un adecuado diagnóstico de la información bibliométrica encontrada, adicionalmente se realizaron mapas bibliométricos basados en autores empleando la herramienta VOSviewer.
Cabe señalar que en este trabajo se han excluido aspectos de resistencia al fuego u otros factores ambientales. La presentación de los resultados se organiza en función de dos aspectos clave identificados en la literatura: los estudios experimentales y la modelación numérica de muros de entramado ligero.
Palabras clave: estructuras de madera, mapas bibliométricos, modelos numéricos, ensayos experimentales, uniones clavadas, elementos finitos, comportamiento no lineal.
Abstract: Due to the damage caused to timber structures during the 1994 Northridge earthquake, research focused on understanding, designing, and improving the seismic response of lightweight timber framed shear walls has experienced a remarkable growth. The main objective of this state-of-the-art review article is to synthesize the innovations and findings found during the last decade, which are detailed in research articles found in the ScienceDirect database. In order to provide a starting point to serve as a reference to explore future lines of research. The methodology indicated in the PRISMA statement has been adopted to give an adequate diagnosis of the bibliometric information found, additionally by using the VOSviewer tool bibliometric maps based on authors were made. It should be noted that aspects of fire resistance or other environmental factors have been excluded in this work. The presentation of the results is organized according to two key aspects identified in the literature: experimental studies and numerical modelling of light-framed walls.
Keywords: Timber structures, bibliometric maps, numerical models, experimental tests, nailed joints, finite elements, nonlinear behavior.
INTRODUCCIÓN
En un edificio de madera los muros de corte junto a los diafragmas horizontales constituyen los elementos primarios del sistema resistente a fuerzas laterales [1]. Un muro de entramado ligero consta de un marco que puede ir desde los 1200 mm de longitud en adelante, con montantes verticales denominados pies derechos — generalmente espaciados a intervalos de 400 mm— junto con elementos horizontales denominados soleras. La escuadría de estos componentes es generalmente de 38 x 89 mm. Por lo general, los marcos tienen un revestimiento (en uno o ambos lados) de paneles de OSB o plywood cuya dimensión varía entre 7 y 15 mm. Estos muros pueden tener adicionalmente un panel de yeso en la cara interior. Los clavos que unen el marco con los pies derechos suelen estar espaciados a lo largo de sus bordes en intervalos de 50, 75, 100 o 150 mm; a esta conexión se le denomina S2F por sus siglas en inglés (sheathing to framing). Además, los muros cuentan con anclajes de sujeción mayormente del tipo hold-down para evitar el vuelco y pernos de corte que sujetan la estructura a la cimentación [5]. La geometría del muro se puede apreciar a detalle en la figura 1 [6].
Se ha experimentado con muros de entramado ligero en los que han variado los siguientes aspectos: i) relaciones de aspecto, ii) espesor de los paneles de revestimiento, iii) espaciamiento del clavado que une el panel al marco, iv) separación entre pies derechos que dan soporte al muro, v) material del panel de recubrimiento y vi) sistema de sujeción empleado [4]. De esta forma, el estudio del comportamiento de muros de corte madera de entramado ligero ha sido de gran interés en las últimas décadas debido a su uso como sistema resistente a fuerzas laterales en estructuras de madera de baja altura [7].
Este artículo de revisión del estado del arte tiene como objetivo sintetizar los resultados de una amplia revisión bibliográfica acerca de las variaciones hechas a las principales características constructivas de muros de entramado ligero de madera, con el propósito de mejorar la respuesta estructural que estos presentan ante la acción de cargas laterales; mismas que se han obtenido mediante ensayos experimentales de laboratorio (monotónicos y cíclicos) con el fin de evaluar su influencia en el comportamiento no lineal de este elemento estructural. En este artículo también se incluye una revisión de los trabajos direccionados al modelamiento numérico de estos muros.
Las conclusiones, hallazgos y resultados descubiertos por los investigadores se presentan de forma pertinente en cada sección que compone los resultados de este artículo, para
ser posteriormente discutidos haciendo énfasis en las limitaciones de la evidencia y cómo estas pueden ser solventadas a partir de nuevas innovaciones y hallazgos. De tal forma, este documento sirve como una referencia valiosa para los autores interesados en explorar futuras líneas de investigación, sobre todo en aquellos países donde el entramado ligero de madera no ha sido estudiado a profundidad y mucho menos es utilizado para edificaciones.
![Geometría típica del muro de corte con entramado ligero de madera, tomada de Lebeda et al. [6]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29350/726177442003_gf5.png)
F igura 1.
Geometría típica del muro de corte con entramado ligero de madera, tomada de Lebeda et al. [6]
MATERIALES Y MÉTODOS
La información recopilada en este artículo se basa en una exhaustiva búsqueda realizada en la plataforma ScienceDirect. Para obtener resultados pertinentes, se empleó una combinación específica de términos de búsqueda: (light+frame AND ((wood OR timber) + “shear wall”)) NOT .“CLT shear wall” OR “post and beam” OR thermal OR fire OR roof OR “cold formed”). Esta instrucción tiene el propósito de excluir artículos que se centren en el estudio de muros construidos completamente con CLT o con el sistema estructural de poste-viga, ya que estos presentan características estructurales diferentes al muro de entramado ligero. Además, se descartaron los términos thermal. fire. Asimismo, se excluyeron los resultados que contenían los términos cold formed . roof ya que también existen sistemas de entramado ligero utilizados en pisos, cubiertas y muros de acero. Finalmente, la búsqueda se limitó a presentar resultados de los diez últimos años, rango comprendido entre 2014 y 2023. Únicamente están incluidos artículos de investigación para garantizar la relevancia y actualidad de la información recopilada en este contexto específico.
En este estudio, se emplea una técnica de análisis cienciométrico conocida como bibliometría, la cual ayuda a representar el dominio del conocimiento y a revelar las relaciones entre artículos, revistas y palabras clave [8]. El programa VOSviewer es una herramienta que facilita la visualización de datos bibliométricos obtenidos de una plataforma de búsqueda de datos [9]. La información extraída permite representar en un mapa bibliométrico los autores encontrados en la primera búsqueda de resultados, como se ilustra en la figura 2. Los autores se organizan con una escala de colores, donde el naranja indica su participación reciente en determinado artículo, mientras que el azul representa los trabajos más antiguos.
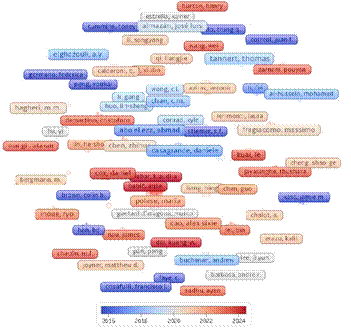
F igura 2.
Mapa bibliográfico basado en autores encontrados en la primera búsqueda en ScienceDirec
Para la revisión sistemática se optó por la metodología indicada en la declaración PRISMA 2020 [10]. En la figura 3 se presenta un diagrama de flujo que ilustra el proceso de selección de estudios. Para el análisis se identificaron inicialmente 116 resultados a través de la base de datos ScienceDirect. Durante la fase de aplicación de criterios de inclusión y exclusión basados en el año de publicación, que se realizó en la misma base de datos limitando los artículos a aquellos publicados a partir de 2014, el número se redujo a 77 registros para revisión. Luego, se excluyeron otros estudios tras revisar criterios como el título, el resumen y las conclusiones, asegurando que estuvieran dentro del ámbito de interés para la revisión, lo que redujo el número a 30 estudios.
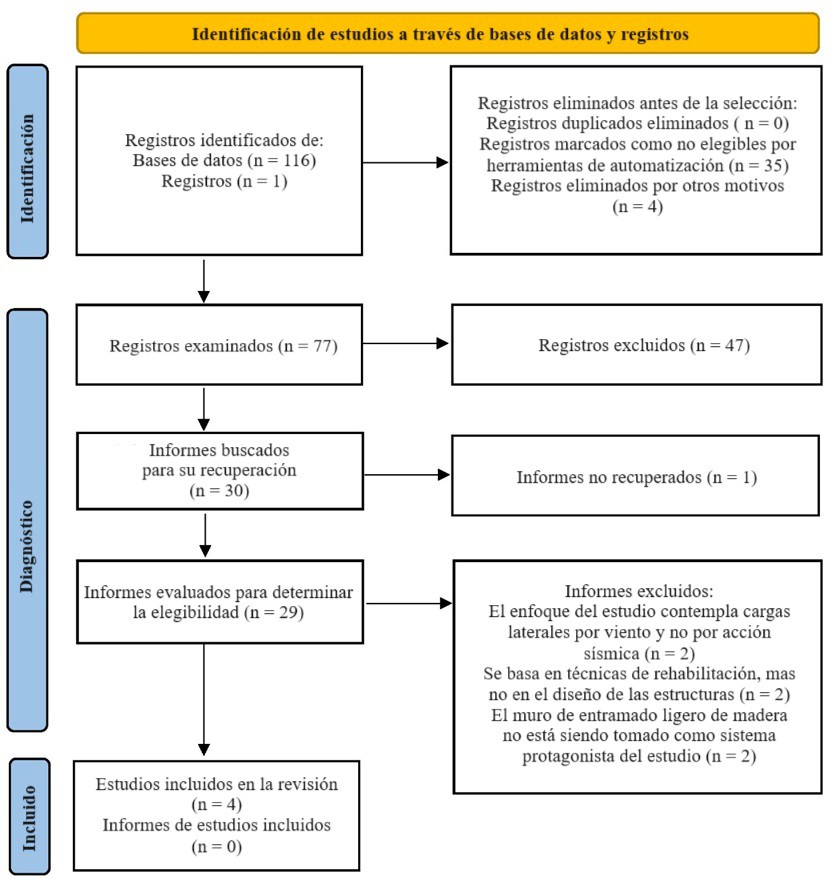
Figura 3.
Flujograma PRISMA que identifica el proceso de selección de datos para la investigación
En la etapa de diagnóstico se excluyeron trabajos de investigación que inicialmente se percibían como objeto de inclusión en la revisión. En primer lugar, se descartaron dos artículos [11,12] debido a que la investigación desarrollada en los mismos está ligada a cargas laterales por la acción del viento y no a la ocurrencia de un sismo. Se desecharon también dos artículos [13,14] enfocados a la rehabilitación de estructuras más que a un diseño experimental de los muros y, por último, estudios en los que los muros no se toman como principal sistema resistente a fuerzas [15,16].
A medida que avanzaba la revisión, se identificaron y añadieron cuatro estudios adicionales [17,18,19,20], que se consideraron pertinentes para la inclusión, ya que seguían las líneas de investigación tratadas en este artículo. En la figura 4 se observa un mapa bibliométrico con los autores considerados en la sección de resultados. Visualmente, se indica cómo han colaborado en sus investigaciones a lo largo de esta última década, pues la escala de colores tiene el mismo significado que el explicado para la figura 2.
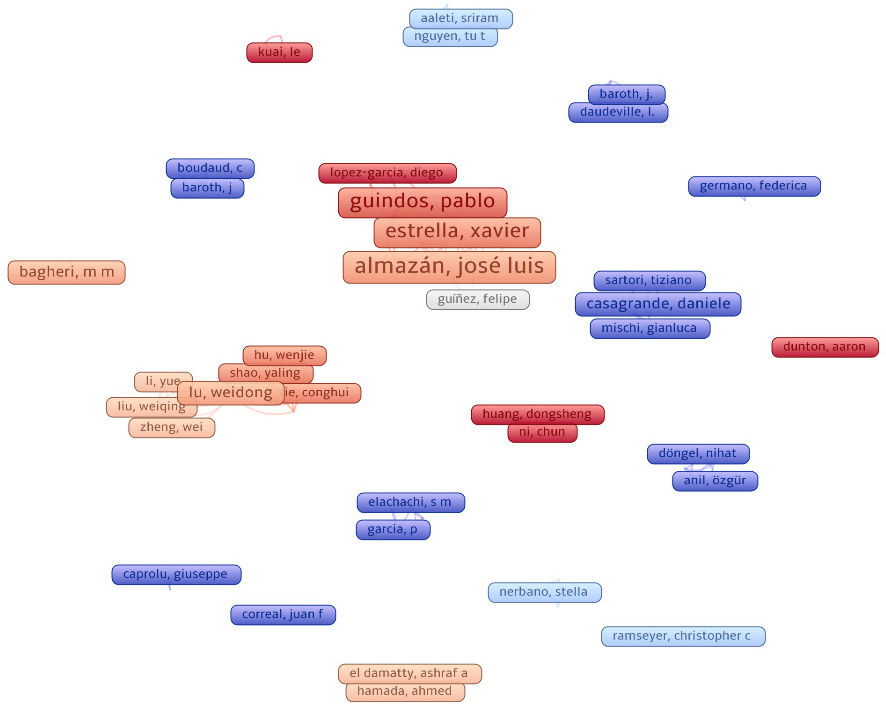
Figura 4.
Mapa bibliográfico basado en autores de la etapa final de búsqueda
RESULTADOS
Una vez realizada la selección final de los artículos y las categorías de organización de estos, se presenta a continuación el trabajo de cada grupo de investigadores en orden cronológico ascendente para cada sección.
Estudios experimentales
En esta primera sección se albergan aquellos estudios experimentales donde los investigadores han analizado la variación de distintos detalles constructivos, mismos que no representan un cambio abrupto respecto a la concepción propiamente de un muro de entramado ligero de madera. Se revisa también estudios de la conexión S2F y la propuesta de materiales alternativos para conformar el marco, los paneles de revestimiento. En estas investigaciones del tipo experimental, los ensayos de laboratorio en los cuales se aplican cargas cuasiestáticas de forma monotónica o cíclica a los especímenes sirven para una posterior evaluación de las propiedades mecánicas. Esto permite identificar si se han alcanzado mejoras en el rendimiento del muro.
Variaciones en la geometría y detalles constructivos de los muros
Los dispositivos de anclaje tipo hold-down evitan el levantamiento vertical del muro al proveer sujeción a la base. En el caso de muros parcialmente anclados, donde estos dispositivos no soportan toda la solicitación, la solera inferior distribuye uniformemente las fuerzas de anclaje generadas por la conexión S2F y los pernos de anclaje. Esto puede provocar flexión transversal al eje principal de la solera inferior, resultando en un posible fallo local frágil e indeseado a nivel global del muro [18]. Caprolu et al. [18] investigaron, de forma experimental y numérica, la capacidad de carga de las soleras inferiores en estos casos, identificando dos modos principales de fallo: división en la parte inferior de la solera y división en el borde en contacto con la conexión S2F. La distancia entre el borde de la arandela del perno de anclaje y la cara de la solera conectada al panel de revestimiento influye en el tipo de fallo; si supera los 10 mm, se produce el primer tipo de fallo. Además, sugieren que orientar la médula del riel hacia abajo, en lugar de hacia arriba, proporciona una mayor resistencia.
Anil et al. [19], llevaron a cabo un estudio experimental sobre la inserción de elementos horizontales resistentes entre los pies derechos distribuidos a lo largo de la altura del muro. Estos elementos, de la misma sección que los componentes principales del marco, condujeron a un notable aumento de resistencia, rigidez, ductilidad y capacidad de disipación de energía. Se analizaron variables como la relación de aspecto y la presencia de aperturas para puertas y ventanas. A pesar de que estas aperturas suelen reducir la capacidad resistente del muro, la inclusión de elementos horizontales contrarrestó estos efectos, incluso reduciendo la longitud de las grietas en las esquinas de las aperturas después del fallo del muro.
Shadravan y Ramseyer [21], investigaron técnicas constructivas para mejorar la resistencia lateral de los muros. Encontraron un aumento del 13,2 % en la capacidad de carga lateral al usar clavos anillados de relación de aspecto 8d, espaciados cada 150 mm en los bordes y 300 mm al centro, con pies derechos espaciados cada 405 mm. También exploraron otras técnicas, como el uso de un doble elemento en la solera inferior del muro, anclado por pernos cada 900 mm y aumentando hasta 3 veces la resistencia. Todos los hallazgos de estos investigadores son con respecto a un muro tradicional mostrado en la figura 1. Asimismo, identificaron incrementos porcentuales en la capacidad de los muros con diversas modificaciones: doble elemento en la solera inferior (122 %), placas de asiento para arandelas (33 %), reducción del espaciamiento entre clavos (28,3 %), uso de clavos anillados (13,2 %) y reducción del espaciamiento entre pies derechos (5,8 %).
Sadeghi et al. [20], realizaron pruebas experimentales en su modelo de muro propuesto, el cual emplea elementos de armazón de madera laminada encolada con una sección de 180 x 180 mm2 en los bordes, superior a la convencional en muros cortantes de entramado ligero de madera. Además, utilizaron un dispositivo de sujeción esquinero robusto y ángulos de conexión de corte para asegurar el muro a la base. Durante el estudio, consideraron espacios libres entre el panel de revestimiento de OSB y los anclajes esquineros, visibles en la figura 5, para prevenir el pandeo prematuro del panel, tanto por cargas sísmicas como por variaciones dimensionales debidas a la humedad. Encontraron, experimentalmente, que la implementación de esta práctica mejora la resistencia al cortante lateral. Concluyeron que es necesario mejorar la conexión entre
los pies derechos de borde y la solera superior, incrementando la rigidez axial al emplear más de dos tornillos en el punto de conexión, mejorando la resistencia al corte y el desplazamiento horizontal durante el estado límite de servicio del muro.
![Espacios libres entre el panel de revestimiento y los anclajes esquineros, tomada de Sadeghi et al. [20]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29354/726177442003_gf11.png)
Figura 5.
Espacios libres entre el panel de revestimiento y los anclajes esquineros, tomada de Sadeghi et al. [20]
Guiñez et al. [5], presentaron los resultados de 17 ensayos, entre monotónicos y cíclicos, aplicados a muros con características distintivas como lo son un conjunto de 5 elementos que componen los pies derechos de borde a cada lado y la disposición de hold-downs de mayor resistencia a los usados comúnmente. Ambas caras son revestidas con paneles de OSB que se clavan al armazón cada 50 o 100 mm en los bordes. Las conclusiones expuestas por los autores informan de un amortiguamiento viscoso equivalente característico del 9 % en promedio para todos los ensayos. Ni el espaciamiento del clavado ni la longitud de los muros influye en la ductilidad que es en promedio 3,75. Al comparar la respuesta de una probeta ante carga cíclica y monotónica, se encuentra que, durante el ensayo cíclico la resistencia al corte se ve reducida entre 8 % y 16 %, donde los muros con clavado de 50 mm tienen una menor afectación. Sin embargo, esta separación no influye en la rigidez del muro, propiedad que es definida por la longitud del elemento estructural. Sus resultados experimentales comparados con los valores teóricos de la SDPWS (Special Design Provision for Wind and Seismic) [22], tienen una mayor resistencia, pero menor rigidez a corte. En referencia al Código de Diseño Sísmico Chileno [23], proponen un aumento del límite de deriva actual hasta un valor de 0,4 %, nivel al cual no se han observado daños a la estructura.
Bagheri y Doudak [4], investigaron el comportamiento estructural de 26 especímenes de prueba con diferentes detalles de construcción y presentaron un modelo numérico analizado en la sección correspondiente del presente trabajo. Las observaciones extraídas por los autores en la parte experimental indican que la adición de más elementos a los pies derechos borde y el cambio de dimensiones de estos no tiene un efecto significativo en la capacidad general del muro, aunque sí un efecto menor sobre la rigidez. Los paneles de revestimiento más gruesos confieren una mayor resistencia y rigidez sin afectar el radio de ductilidad, independientemente del material (plywood u OSB). Si bien se ha encontrado que el diámetro de los clavos y el espaciamiento afecta significativamente la resistencia, no hay una relación lineal que describa este efecto.
Orellana et al. [3], investigaron el comportamiento de muros de corte con marcos de madera chilena calificada MGP10 a escala real. Estas muestras tenían una altura de 2470 mm y se probaron en tres longitudes diferentes: 1200, 2400 y 3600 mm. Encontraron
que la capacidad máxima de carga lateral aumentó en promedio un 37 % respecto a lo presentado por Guiñez et al. [5], (variando entre el 8 % y el 63 %) cuando se aplicó carga axial de compresión y momento volcante además de la carga netamente horizontal. Asimismo, la rigidez inicial mostró un incremento del 141 % (variando entre el 103 % y el 191 %), mientras que la capacidad de disipación de energía aumentó un 104 % (variando entre el 36 % y el 156 %). Por último, la relación de ductilidad experimentó un aumento del 55 % (variando entre el 22 % y el 87 %).
Estrella et al. [24], llevaron a cabo pruebas para evaluar el comportamiento de cuatro muestras con diferentes configuraciones bajo condiciones laterales, utilizando sujeciones de varillas continuas, en comparación con muros sujetos a anclajes discretos. Los resultados de su investigación indican que el uso del sistema de varilla continua aumenta la resistencia del muro en un 35,8 % y permite un comportamiento elástico hasta derivas aproximadas de 0,8 %. Además, al reducir el espacio de clavado de 100 a 50 mm en una de las configuraciones, se observó un incremento del 21,7 % en la rigidez y un aumento del 40 % en la resistencia. Aunque el diámetro de la varilla no tuvo un impacto significativo en estos parámetros, se encontró que el uso de una varilla de mayor diámetro (44,5 mm) y una configuración de clavado con un espaciado de 50 mm aumentó la ductilidad hasta 6,32 en uno de los especímenes.
Qiang et al. [25], presentan una variación constructiva al conectar los paneles de revestimiento al marco con tres filas de clavos en lugar de una sola alrededor de los bordes. Tras ensayos cíclicos en 10 especímenes, se encontró una resistencia lateral hasta tres veces más que la de muros estándar. También se observaron mejoras en la rigidez inicial y la deformación a la falla. Los autores llevaron a cabo una equivalencia sísmica con los muros estándar según la normativa ASTM D7989 [26]. En este procedimiento determinaron valores de diseño que resultaron ser menos del doble que los correspondientes a muros estándar. Esta aparente contradicción se justifica por la necesidad de aplicar un factor de sobreresistencia mayor que garantiza el cumplimiento de los criterios de ductilidad establecidos en la normativa de referencia.
Conexión entre armazón y panel de revestimiento, conexión S2F
El entendimiento de la histéresis en las conexiones entre el armazón y el panel de recubrimiento es crucial para comprender la respuesta dinámica de las estructuras de madera, ya que permite calcular la cantidad de energía disipada. Según Lam et al. [1], este comportamiento complejo surge debido a la fluencia de los sujetadores (generalmente clavos), las propiedades de la madera en el muro y la formación de espacios holgados en los puntos de conexión como resultado de la acción dinámica. A medida que la carga actuante varía, el sujetador ejerce presión sobre la madera en el área de contacto, causando deformaciones permanentes. Al invertir la carga, el sujetador se desplaza a través del espacio creado, generando holguras en sentido opuesto, en un proceso cíclico que incrementa estas aperturas a cada paso, resultando en una deformación flácida y una apariencia de “pellizco” (pinching) en el bucle de histéresis.
La conexión S2F puede realizarse también empleando grapas en lugar de la forma más común: por medio de clavos. Verdret et al. [27], estudiaron la orientación de las grapas en relación con las fibras del armazón, utilizando OSB de 12 mm y elementos
de armazón de madera C24 (45 x 145 mm²). Determinaron que las grapas deben tener dimensiones específicas para ser comparables con clavos roscados según el Eurocódigo 5 [28]. Los ensayos monotónicos mostraron que las conexiones grapadas a 0° tienen un 20 % menos de capacidad de carga que las orientadas a 90° y que las clavadas, también ensayadas para efectuar comparaciones. Sin embargo, las grapas a 0° mostraron mayor rigidez debido al anclaje con el pie derecho. Además, la velocidad de carga en ensayos cíclicos afectó la carga máxima observada en las conexiones clavadas, mientras que las grapadas resultaron menos afectadas en términos de ductilidad evaluada según la normativa ASTM E 2126 [29].
Germano et al. [30], investigaron el impacto de la superficie del vástago en conexiones clavadas, comparando clavos lisos con anillados. Descubrieron que, para un diámetro de clavo equivalente, la resistencia de las conexiones con clavos anillados es 1,75 veces mayor que las de superficie lisa. A pesar de observar una disminución en la rigidez inicial con clavos anillados debido a las holguras que provocan las estrías en la madera, los autores sugieren que se necesitan más estudios para evaluar completamente este efecto.
Zheng et al. [31], realizaron un estudio sobre conexiones utilizando tornillos autorroscantes y paneles de ply-bamboo. Aunque el uso de este material podría ubicar el estudio en el apartado de materiales alternativos para armazón y revestimiento, las conclusiones presentadas por los investigadores justifican su inclusión en esta sección. Realizaron ensayos monotónicos en veinte grupos de conexiones con ply-bamboo atornilladas a un elemento de armazón (ply-bamboo sheathing-to-framing screwed, PSFS) y dos grupos adicionales de conexiones tradicionales clavadas con paneles de OSB. Los resultados indicaron que el uso de tornillos autorroscantes proporciona una resistencia y desplazamiento últimos 2,5 y 2 veces mayores que las conexiones tradicionales con clavos y paneles de OSB. Además, destacan que el espesor del panel de ply-bamboo y la distancia al tornillo no afectan significativamente las propiedades mecánicas, como sí lo hace la dirección de carga con respecto a las fibras de la madera del marco, donde se observa mayor rigidez, resistencia y ductilidad en la orientación paralela. Los autores atribuyen las variaciones principalmente a vacíos e imperfecciones en el ply-bamboo.
Materiales alternativos en elementos de marco y paneles de revestimiento
Echeverry y Correal [32], proponen el uso de guadua laminada (Laminated Guadua Mats, LGM) para los elementos del marco y paneles de revestimiento. Su estudio evalúa experimentalmente el comportamiento no lineal de conexiones S2F compuestas de clavos y LGM, utilizando dos tamaños diferentes de clavos y aplicando la carga en dirección paralela y perpendicular a las fibras del panel de revestimiento. Observaron una mejor respuesta con clavos de mayor tamaño. Además, desarrollaron un modelo numérico con el software CASHEW [33], para evaluar el potencial de los muros de corte fabricados completamente de LGM, basándose en los resultados de los ensayos de las conexiones. Afirman que estos muros tendrían una capacidad similar a los fabricados con materiales tradicionales como la madera. Señalan también que las pequeñas diferencias en rigidez y resistencia se deben a variaciones en la calidad de la LGM, atribuibles a procesos de fabricación que deben ajustarse para eliminar vacíos e imperfecciones.
Nguyen et al. [34], llevaron a cabo una investigación experimental sobre la integración de pies derechos postensados de madera contra laminada (CLT) en un muro híbrido de 5486 mm de largo por 2438 mm de alto. El sistema, ilustrado en la figura 6, consta de tres muros tradicionales, donde dos de ellos se conectan mediante seis clavos normales (por cada muro) de relación 16d (89 x 3,43 mm) que anclan los pies derechos de borde al elemento compuesto por cinco capas de CLT (133 x 610 x 2440 mm). Se aplicó una fuerza de 97,86 kN para ejecutar el postensado mediante 7 cables de acero (Fy = 1530 MPa) de 12,7 mm de diámetro colocados a lo largo de un ducto al interior del panel de CLT. El estudio evalúa el comportamiento sísmico del sistema y concluye que se desempeña bien ante el MCE (máximo terremoto considerado), con una deriva máxima inferior al 1 %. Se atribuye este resultado a la alta rigidez y eficiente capacidad de autocentrado proporcionadas por el CLT postensado, complementadas con la disipación de energía de los muros tradicionales. Por ello, los autores sugieren este sistema como una solución para edificaciones residenciales de mediana a gran altura.
![Sist ema de muro híbrido CLT - Light frame, tomada de Nguyen et al. [34]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29355/726177442003_gf13.png)
Figura 6.
Sist ema de muro híbrido CLT - Light frame, tomada de Nguyen et al. [34]
Yue et al. [35], realizaron una investigación experimental con cinco muros a escala real (2400 x 2400 mm) utilizando madera tipo plywood densificada, fabricada con chapas de álamo de 2 mm de espesor, prensadas a 130 °C con adhesivo de fenol-formaldehído, logrando densidades de 550, 650 y 840 kg/m³ mediante la colocación ortogonal de 7, 9 y 12 chapas de álamo, respectivamente. Se evaluó la factibilidad de la madera densificada como revestimiento de muros y su impacto en el desempeño lateral mediante ensayos monotónicos. Se observó una mejora en el rendimiento lateral con el aumento de la densidad del revestimiento, destacando el mejor desempeño del espécimen con densidad de 840 kg/m³. Además, se constató que el rendimiento de un muro con un panel marginalmente densificado es cercano al de uno completamente densificado, evitando el desgarro del revestimiento y focalizando el daño hacia los conectores (clavos). Al comparar los resultados experimentales con el modelo elastoplástico de Casagrande et al. [36], se encontró un error de aproximadamente el 10 %, sugiriendo la utilidad de este modelo en el diseño de muros con este tipo de revestimiento.
Valdivieso et al. [37], investigaron cómo los acabados no estructurales afectan las propiedades de un muro compuesto por múltiples capas (MLSSW). Utilizaron paneles
de yeso Tipo X (GWB) para revestir un MLSSW y compararon con uno sin revestimiento. Los acabados aumentaron la resistencia (160 %) y rigidez (53 %), aunque la ductilidad disminuyó (16 % - 42 %). Aun así, la energía disipada fue comparable a la de los muros sin revestimiento. En resumen, los muros con acabados tienen características histeréticas similares a los muros sin revestimiento.
Estudios numéricos
En la presente sección se contemplan análisis, metodologías, enfoques y modelos propuestos por los investigadores citados para el desarrollo de un modelado no lineal y diseño de los muros de madera estudiados en forma efectiva. Dentro de esto se puede encontrar modelos que caracterizan el comportamiento histerético de las conexiones S2F para incorporarlos a enfoques de modelado no lineal basado en elementos finitos (FE). Dada la complejidad de los modelos, algunos autores proponen simplificaciones para representar estructuras de varios niveles con resultados de análisis aceptables. Las investigaciones en el diseño de muros parten de la propuesta de estos elementos en edificaciones de mayor altura, expuestas a solicitaciones verticales y horizontales en el caso de zonas de alta sismicidad.
Enfoques de modelado
Humbert et al. [38,39], presentaron un estudio en dos partes. En la primera, desarrollaron un modelo de elementos finitos calibrado mediante ensayos de laboratorio para determinar los parámetros del modelo histerético que se muestra en la figura 7, mismo que describe el comportamiento no lineal de las uniones S2F, representadas dentro del modelo de elementos finitos por medio de resortes de conexión entre dos nodos.
![FigLey constitutiva de histéresis empleada por Humbert et al. para modelar el comportamiento no lineal de las conexiones S2F [38]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29356/726177442003_gf14.png)
Figura 7.
FigLey constitutiva de histéresis empleada por Humbert et al. para modelar el comportamiento no lineal de las conexiones S2F [38]
El arreglo completo se muestra en la figura 8, donde se tiene además elementos tipo viga Euler para dar forma al marco y elementos de tensión en el plano que conectan 4 nodos para dar forma al revestimiento. Validaron el modelo con 14 muros sometidos a carga cuasiestática en ensayos monotónicos y cíclicos, encontrando una buena concordancia entre las predicciones del modelo de elementos finitos y los experimentos reales.
![Composición del modelo complejo de elementos finitos propuesto por Humbert et al. [38]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29357/726177442003_gf17.png)
F igura 8.
Composición del modelo complejo de elementos finitos propuesto por Humbert et al. [38]
Boudaud et al. [38,39], en su segunda investigación, validaron su modelo de elementos finitos bajo carga dinámica, utilizando 11 muros de corte en una mesa vibratoria. Con los resultados de su investigación anterior ante carga cuasiestática calibraron el modelo para carga dinámica, obteniendo una buena concordancia entre los resultados experimentales y los del modelo. Proponen una simplificación a su modelo, consistente en cuatro elementos de marco rígidos, un elemento de conexión semirrígido, dos masas concentradas y dos amortiguamientos, como se ve en la figura 9. Esta simplificación, aunque menos compleja, ofrece resultados comparables al modelo original con una reducción significativa en esfuerzos computacionales, lo que la hace un método eficiente para modelar muros de una edificación completa.
![F igura 9. Composición del modelo de elementos finitos simplificado propuesto por Boundad et al. [39]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29358/726177442003_gf20.png)
[9]
F igura 9. Composición del modelo de elementos finitos simplificado propuesto por Boundad et al. [39]
Figura 9. Composición del modelo de elementos finitos simplificado propuesto por Boundad et al. [39]
Casagrande et al. [17], proponen la Ec. 1 para describir el comportamiento elástico de muros de un solo nivel, considerando la contribución a la deformación lateral de la conexión S2F (Δsh), la rotación (Δ.), la traslación de cuerpo rígido (Δ.) y la deformación de los paneles de revestimiento (Δ.). Se identifica que las mayores contribuciones a la deformación total en muros de entramado ligero son de las conexiones S2F y la rotación de cuerpo rígido, asociada a la deformación por tensión de los hold-downs. Además, se aborda el análisis de la rigidez en dos regímenes: uno donde los hold-downs son insignificantemente solicitados y otro donde sí están siendo solicitados. La relación que expresa la rigidez en este último caso se formula en la Ec. 2, donde se evidencia que la rigidez total depende de los mismos parámetros que caracterizan la deformación. Los investigadores concluyen que la rigidez del muro es linealmente proporcional a su longitud, pero esta relación solo es válida durante el primer régimen de rigidez.
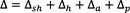
(1) [17]
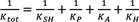
(2) [17]
Peng et al. [40], desarrollaron un modelo simplificado de elementos finitos para analizar muros de corte de madera de uno y varios niveles. Este modelo, representado en la figura 10, consta de elementos de conexión laterales conectados por una viga rígida, simulando cada piso del muro.
![F igura 10. Composición del modelo de elementos finitos simplificado propuesto por Peng et al. [40]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29359/726177442003_gf21.png)
[10]
F igura 10. Composición del modelo de elementos finitos simplificado propuesto por Peng et al. [40]
Se incorporan resortes de compresión, corte y tensión, derivados de un modelo numérico detallado que simula todos los componentes del muro. Los resultados muestran diferencias mínimas entre el modelo simplificado y el detallado. Por ejemplo, para muros de un solo nivel, las diferencias en rigidez inicial y fuerza cortante pico son del 2,88 % y 0,48 %, respectivamente. Sin embargo, al considerar muros de cuatro niveles, estas diferencias aumentan al 15 % y 13,2 % en muros sin varillas de sujeción, aunque se reducen al 6,7 % y 1,4 % al incluir estos dispositivos. Por lo tanto, los autores concluyen que el modelo simplificado es aceptable debido a la significativa reducción en el tiempo de cálculo y esfuerzo de modelado, lo que lo hace una herramienta práctica y eficiente para el análisis de muros de corte de madera.
Estrella et al. [2], proponen un enfoque simplificado para modelar muros de alta resistencia, centrándose en características especiales como pies derechos de borde robustos y hold-downs de baja deformación. Su método se basa en la medición de deformaciones diagonales debidas a cargas laterales cíclicas para obtener los diez parámetros del modelo MSTEW [41], los cuales se presentan en la tabla 1, considerando diferentes configuraciones constructivas. Este modelo permite que un resorte no lineal de un solo grado de libertad (SDOF) represente el comportamiento del muro completo. Al examinar las conexiones S2F, los autores observan que las esquinas del panel son áreas críticas que demandan más deformación y disipación de energía. Por lo tanto, proponen ajustar el patrón de clavado para mejorar la resistencia. No obstante, aún no se ha llevado a cabo una validación experimental de esta modificación.
Tabla 1. Parámetros para el modelado no lineal en un solo grado de libertad (SDOF), en base al modelo histerético MSTEW de un muro de entramado ligero de madera propuestos por Estrella et al. [2]
| PropiedadesParámetrosparaelmodelohisteréticoMSTEW del muro | |||||||||||
| OSB | Espaciamiento del clavado (mm) | Ko (kN/ mm/m) | r1 | r2 | r3 | r4 | Fo (kN/m) | F1 (kN/m) | δu (mm) | α | β |
| A un solo lado | 50 | 2,374 | 0,072 | -0,046 | 1,000 | 0,017 | 10,275 | 2,048 | 45,450 | 0,532 | 1,139 |
| 100 | 1,393 | 0,079 | -0,101 | 1,047 | 0,015 | 9,600 | 1,603 | 57,300 | 0,531 | 1,146 | |
| 150 | 1,080 | 0,079 | -0,090 | 1,075 | 0,014 | 7,104 | 1,202 | 55,820 | 0,522 | 1,150 | |
| A ambos lados | 50 | 2,487 | 0,097 | -0,080 | 1,002 | 0,021 | 26,685 | 2,935 | 42,887 | 0,800 | 1,150 |
| 100 | 2,786 | 0,079 | -0,101 | 1,047 | 0,015 | 19,196 | 3,205 | 57,300 | 0,531 | 1,146 | |
| 150 | 2,159 | 0,079 | -0,090 | 1,075 | 0,014 | 14,208 | 2,403 | 55,820 | 0,522 | 1,150 | |
Kuai et al. [42], desarrollaron un nuevo modelo numérico de un conector elastoplástico para representar la conexión S2F, integrándolo en un modelo de elementos finitos (FE) previamente desarrollado [43]. Este modelo se probó en dos muros de corte a escala real sometidos a carga cíclica, comparándolos con simulaciones. Los resultados mostraron que los conectores pueden prever tanto deformaciones elásticas como inelásticas bajo cargas cíclicas, con una precisión razonable en la predicción de dichas deformaciones. Además, se observó que la ubicación de la concentración de tensión crítica en los paneles de revestimiento coincidió con los puntos de fractura en las paredes de prueba. A partir de estas simulaciones, se concluyó que la rigidez y resistencia a la estantería de los muros de corte de doble capa pueden aproximarse a partir de los resultados de paredes de una sola capa. Sin embargo, debido a la complejidad del desarrollo del modelo de conexión, se sugiere consultar la publicación original para más detalles.
Dunton et al. [44], desarrollaron modelos probabilísticos basados en ensayos experimentales para predecir la fuerza cortante y la deriva en muros cortantes de marcos ligeros de madera. Estos modelos ajustan las predicciones de fuerza cortante a los valores del código SDPWS [22] tras corregir el sesgo. Este modelo tiene la ventaja de incorporar la física de la deformación y desacoplar la contribución de las capacidades individuales de los clavos. Aunque los modelos de capacidad de deriva tienen desviaciones estándar mayores debido a la falta de información detallada sobre algunos componentes, representan una mejora sustancial respecto a los modelos deterministas. Se recomienda revisar las expresiones analíticas en la publicación original para una comprensión más detallada
Enfoques de diseño
La investigación realizada por Caprolu et al. [18], se centra en evaluar expresiones previamente desarrolladas [45,46], determinando la capacidad de carga resistente antes de que se produzca la división en la solera inferior. Con base en datos de ensayos experimentales de ruptura de este elemento [47,48], llevaron a cabo pruebas de energía de fractura y resistencia a la tensión perpendicular a la fibra. Estas pruebas son cruciales, ya que los resultados obtenidos son valores esenciales para evaluar las expresiones
numéricas. Los autores indican que la carga asociada a la falla por división de la cara inferior de la solera se determina mediante la Ec. 3, mientras que el segundo modo de falla se aborda mediante la Ec. 4. Los parámetros utilizados en estas ecuaciones se presentan en las figuras 11 y 12.
![Figura 11. Parámetros geométricos de la Ecuación 3, la cual determina el fallo de la solera base por ruptura en la cara inferior, tomada de Caprolu et al. [18]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29360/726177442003_gf23.png)
[11]
Figura 11. Parámetros geométricos de la Ecuación 3, la cual determina el fallo de la solera base por ruptura en la cara inferior, tomada de Caprolu et al. [18]
![F igura 12. Parámetros geométricos de la Ecuación 4, la ruptura de la solera inferior ocurre perpendicular a la carga “P”, a una distancia “he” desde el borde superior del elemento, tomada de Caprolu et al. [18]](https://revistas.usfq.edu.ec/index.php/avances/article/download/3270/version/4589/3763/29361/726177442003_gf25.png)
[12]
F igura 12. Parámetros geométricos de la Ecuación 4, la ruptura de la solera inferior ocurre perpendicular a la carga “P”, a una distancia “he” desde el borde superior del elemento, tomada de Caprolu et al. [18]
Es importante destacar que algunos de estos parámetros no están visibles en los gráficos, por lo que se proporcionan explicaciones claras: . corresponde a la longitud de la solera, . es el módulo de resistencia a corte, es la energía a la fractura, . es el módulo de elasticidad, βses el factor de corrección por cortante, y ft es la resistencia a tracción perpendicular a la fibra.
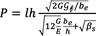
(3) [18]
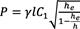
(4) [18]
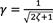
(5) [18]
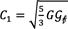
(6) [18]
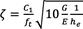
(7) [18]
Bagheri y Doudak [7], investigaron muros de dos niveles para evaluar los efectos acumulativos (deflexión lateral y la rotación de cuerpo rígido), en la deflexión total. Al estimar la deflexión basándose en la suposición de efectos acumulativos, observaron ligeras diferencias con las observaciones experimentales, las cuales no consideran la rigidez fuera del plano de los diafragmas de piso. Los mayores efectos acumulativos provienen de la rotación por cuerpo rígido, generada por la elongación de los hold-downs. Su modelo numérico confirmó que esta suposición es válida para muros apilados sin considerar la rigidez fuera del plano de los diafragmas. Señalaron que las expresiones de diseño tienden a sobreestimar ligeramente la deflexión, especialmente en niveles superiores, debido al significativo efecto de la rigidez fuera del plano de los diafragmas que no está considerado dentro de la expresión. Este efecto persiste incluso con valores conservadores de mínima rigidez fuera del plano o la sola presencia de vigas de borde. La deflexión total esperada por efectos acumulativos para el segundo nivel de piso Δ.2, se determina mediante la Ecuación 8,
donde Δ1 y Δ2 representan las deflexiones singulares de cada piso, Δbc, es la deflexión por
flexión y Δac por rotación de cuerpo rígido.
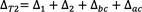
(8) [7]
Orellana et al. [3], realizaron un análisis numérico para una estructura de madera de cinco pisos con el fin de considerar los efectos de las cargas verticales al diseñar, siendo que no existe un procedimiento estándar para hacerlo en construcciones para estructuras de madera. En su investigación representan la estructura con dos análisis no lineales. Para la creación de los modelos se reprodujo la respuesta lateral que se prueba en su estudio experimental, empleando el modelo CASHEW [33] y la no linealidad se introdujo a través de las conexiones S2F empleando el modelo MSTEW [41]. Tras el resultado del análisis señalan que las cargas verticales elevadas pueden tener un impacto relevante sobre el comportamiento lateral, aumentando la capacidad del edificio en sus ejes X y Y un 51,4 % en promedio e incrementando la rigidez inicial del 20,7 %. También obtuvieron una mayor ductilidad y la disminución de las derivas de piso, determinando que la estructura mejora su comportamiento cuando se consideran las cargas verticales.
Estrella et al. [49], llevaron a cabo una investigación basada en experimentación y desarrollo de modelos numéricos para proponer factores de desempeño sísmico (SPFs) menos restrictivos para edificios con estructuras de madera. Como resultado de su investigación observaron que una adopción de R = 6,5 como valor modificador de respuesta y una deriva máxima de piso Δmax = 0,004, en lugar de los valores de referencia R = 5,5 y Δmax = 0,002, representan una reducción del 15,3 % en el índice de margen de colapso promedio de los grupos de especímenes bajo estudio, sin que ninguno de ellos mostrara una probabilidad de colapso mayor al 10 % para aceleraciones correspondientes al máximo terremoto considerado (MCE). La utilización de SPFs menos conservadores mejora la rentabilidad de las estructuras de madera y puede aumentar su competitividad con respecto a otros materiales. El nuevo conjunto de SPFs resulta en un ahorro del 40,4 % en el patrón de clavado de paneles OSB, un 15,9 % en paneles OSB y un 7,3 % en vigas de madera para un estudio de caso de un edificio de cinco pisos.
Berwart et al. [50], han estudiado la viabilidad del sistema estructural en zonas sísmicas de alta demanda, desarrollando la metodología simplificada STTP (Simplified Toll for Technical Pre-feasibility). Esta herramienta, dirigida a profesionales con poca experiencia en madera, requiere solo el cálculo de parámetros geométricos y la aplicación de factores de penalización. Introducen el concepto de longitud ficticia, que se basa en la relación entre la longitud real y una reducida, considerando la pérdida de rigidez del muro. La metodología, basada en el análisis de 201 edificaciones, permite estimar el periodo fundamental del muro y calcular el cortante basal de diseño. Se evalúa la viabilidad técnica del número de metros lineales proyectados y el tipo de dispositivos de anclaje adoptados, con valores máximos sugeridos para edificaciones de tres a seis pisos. Esta metodología no reemplaza el diseño estructural final, sino que sirve como etapa de prediseño, proporcionando información sobre el tipo de dispositivo de anclaje necesario.
DISCUSIÓN
Con respecto a la sección: Estudios experimentales
Interpretación general de los resultados
Los estudios revisados en las tres divisiones de esta primera sección proporcionan una comprensión detallada de diversos aspectos relacionados a los muros de entramado ligero de madera. En la primera parte, se destacan las variaciones en la geometría y los detalles constructivos de los muros, mostrando cómo diferentes enfoques pueden mejorar la resistencia, rigidez y capacidad de disipación de energía de estos sistemas. Se identifican prácticas como la inclusión de elementos horizontales resistentes [19] y el empleo de técnicas constructivas mejoradas [21], así como la influencia del tipo de dispositivo de sujeción [24] y la orientación de los elementos del armazón en el rendimiento estructural [18].
Luego de esto, se profundiza en la conexión entre el armazón y el panel de revestimiento, destacando la importancia de comprender la histéresis en estas conexiones para calcular la cantidad de energía disipada [1]. Se analizan diferentes tipos de sujetadores y su efecto en la resistencia y rigidez de las conexiones, así como la influencia de la
velocidad de carga en el comportamiento estructural [27]. Se exploran opciones como el uso de grapas [27], tornillos autorroscantes [31] y clavos anillados [30] para mejorar el rendimiento de estas conexiones.
Por último, dentro de las mejoras al rendimiento estructural, se examina el uso de materiales alternativos en elementos de armazón y paneles de revestimiento. Se destacan materiales como la guadua laminada [32], el CLT postensado [34] y la madera densificada [35] como opciones viables para mejorar el rendimiento estructural y sísmico de los muros de corte de madera. En resumen, los estudios revisados ofrecen una visión integral de cómo mejorar el rendimiento sísmico y la durabilidad de los muros de entramado ligero de madera, destacando la importancia de considerar cuidadosamente los detalles constructivos, las técnicas de conexión y la elección de materiales para lograr estructuras seguras y eficientes.
Limitaciones de la evidencia
En los estudios expuestos en el apartado de variaciones a la geometría y detalles constructivos de los muros, se evidencia que las pruebas se hacen con carga cuasiestática monotónica o cíclica [3,4,5,19,21,24,25]. No se ha encontrado, al menos dentro de las limitaciones de búsqueda en esta investigación, que los prototipos propuestos por los distintos autores hayan sido sometidos posteriormente a ensayos donde se emplee una mesa vibratoria para determinar su comportamiento bajo excitación sísmica.
Al explorar el uso de materiales alternativos en elementos de armazón y paneles de revestimiento, se destaca la limitación en cuanto a la falta de datos a largo plazo sobre el rendimiento y la durabilidad de estos materiales en aplicaciones estructurales [32,35]. Aunque se presentan resultados prometedores sobre el comportamiento de estos materiales en pruebas experimentales, la falta de información sobre su comportamiento a lo largo del tiempo podría limitar su adopción generalizada en la práctica [32,35].
Implicaciones de los resultados en la práctica, políticas e investigaciones futuras
Orientados hacia la práctica dentro de la ingeniería estructural, los estudios resaltan la importancia de considerar cuidadosamente la geometría y los detalles constructivos de los muros de entramado ligero de madera, así como la elección adecuada de materiales y técnicas de construcción [21]. Se sugiere la adopción de técnicas específicas, como la incorporación de elementos horizontales resistentes y la mejora de las conexiones entre los elementos estructurales, para mejorar la resistencia y la capacidad de disipación de energía de los muros. En cuanto a las implicaciones políticas, los autores citados en ambas secciones de este artículo subrayan la necesidad de actualizar y mejorar las regulaciones y códigos de construcción relacionados con las estructuras de madera [3,5,27,30,49].
En términos de investigación futura, haciendo referencia a las limitaciones de la evidencia, se sugiere la implementación de ensayos sobre mesa vibratoria a prototipos de escala real o reducida. Así mismo, autores han reportado tipos de falla característicos en la conexión S2F al termino de los ensayos, entre los cuales se tiene el aplastamiento del panel de revestimiento provocado por la cabeza del conector [2,3,5]. Resulta necesario contar con innovaciones para prevenir este efecto, pues la conexión S2F es protagonista
del comportamiento global del muro y, asegurar su óptimo funcionamiento, conlleva a una menor degradación de rigidez y resistencia. Por otra parte, hallazgos que nacen de modelos analíticos pueden ser comprobados experimentalmente, tal es el caso del patrón de clavado optimizado propuesto por Estrella et al. [2].
Limitaciones de los procesos de revisión utilizados
De forma general para ambas secciones, seleccionar ScienceDirect como única fuente de consulta y limitar la búsqueda a artículos indexados y revisados por pares puede mitigar algunas barreras en los procesos de revisión. Al utilizar una base de datos confiable y respetada en la comunidad académica, se reduce en gran medida el riesgo de sesgo de selección y se aumenta la probabilidad de encontrar estudios de alta calidad y relevancia. Los artículos revisados por pares suelen someterse a un riguroso proceso de evaluación por parte de expertos en el campo, lo que ayuda a garantizar la calidad y fiabilidad de la información presentada.
Además, al demarcar la búsqueda a artículos de investigación publicados en los últimos 10 años, se asegura que la revisión esté basada en la evidencia más actualizada y relevante disponible en la literatura científica. Esto permite capturar los avances más recientes en el campo y garantizar que los hallazgos y conclusiones discutidos sean pertinentes y aplicables en el contexto actual.
Con respecto a la sección: Estudios numéricos
Interpretación general de los resultados
La investigación sobre muros de entramado ligero de madera aborda aspectos clave en el análisis y diseño estructural, con un enfoque en modelos numéricos avanzados y nuevas metodologías analíticas. En la primera división, los estudios revisados se centran en el desarrollo y validación de modelos numéricos de elementos finitos, mismos que los autores señalan como los más precisos, pero a la vez computacionalmente más demandantes [38,39,40,42]. De forma paralela sucede en la propuesta de modelos simplificados para representar el comportamiento estructural de los muros de madera [2,17]. Todos estos muestran una buena concordancia con los resultados experimentales y ofrecen una variedad de enfoques eficientes para analizar el comportamiento de los muros bajo diferentes condiciones de carga.
En la siguiente división se destacan innovaciones analíticas enfocadas en aspectos específicos del diseño estructural, como la evaluación de la capacidad de carga resistente [18], los efectos acumulativos en la deflexión total de los muros [7] y la integración de cargas verticales en el análisis sísmico [3]. Estos estudios ofrecen nuevas perspectivas sobre cómo mejorar la precisión y eficiencia en el diseño de muros de madera, así como la evaluación de su comportamiento bajo cargas sísmicas. En conjunto, estas secciones reflejan un progreso significativo en la comprensión y aplicación de técnicas avanzadas para el análisis y diseño de los muros en estudio.
Limitaciones de la evidencia
Una de las limitaciones es la falta de validación experimental exhaustiva de los modelos propuestos. Pese a que varios estudios incluyen pruebas experimentales para comprobar sus enfoques [2,38,39,42], es necesario ampliarlas tomando en cuenta la implementación de materiales distintos a los ya ensayados, tanto para la madera del marco, como para el panel de revestimiento o el tipo de conector.
Además, se observa una tendencia hacia la simplificación de los modelos para reducir el esfuerzo computacional. Aunque es comprensible dada la complejidad de los modelos de análisis no lineal [38,39,40,42], estas simplificaciones pueden introducir cierto grado de incertidumbre en las predicciones, especialmente si no se evalúan cuidadosamente sus limitaciones y su impacto en los resultados finales. Asimismo, algunas suposiciones simplificadas, como la falta de consideración de la rigidez fuera del plano de los muros, pueden distorsionar la representación del comportamiento real de los muros de madera.
Implicaciones de los resultados en la práctica, políticas e investigaciones futuras
En la práctica, los avances de modelado numérico ofrecen herramientas más precisas y eficientes para el diseño y análisis de estos muros [17,18,50]; mismas que pueden ser incorporadas dentro de softwarescomerciales [2], pero también en aplicativos de código abierto como OpenSees. En términos de investigación futura, el efecto de la carga vertical sobre el comportamiento del muro ha sido un foco de interés encontrado en esta revisión. Esta es una condición ensayada de forma experimental por los autores y se relaciona al uso de este sistema estructural para edificaciones de mediana altura [2,3]. Extender una gran cantidad de pruebas experimentales a muros de varios niveles representa una gran demanda de recursos, en tanto que los modelos numéricos serán una alternativa para promover innovaciones en el análisis y diseño, particularizando los detalles a tomar en cuenta para cada nivel de piso.
CONCLUSIÓN
Los análisis experimentales y numéricos realizados por los investigadores abordados en este estudio del estado del arte proporcionan avances significativos en la comprensión y mejora del comportamiento estructural de los muros de entramado ligero de madera. En la parte experimental se ha destacado la importancia de considerar cuidadosamente los detalles constructivos, la conexión S2F y la elección de materiales para mejorar el rendimiento sísmico y la durabilidad de estos muros. Por otro lado, los estudios numéricos han avanzado en el desarrollo de modelos precisos y eficientes para el análisis y diseño. Varios de los trabajos se complementan en ambas formas, puesto que los autores desarrollan las dos para validar los hallazgos encontrados. Sin embargo, no todos los detalles constructivos y condiciones de carga han sido explorados, por lo que representan una fuente para futuras investigaciones; particularmente el estudio de la conexión S2F, que es protagonista del comportamiento no lineal del muro ante carga lateral, producto de la acción sísmica. Las futuras investigaciones encaminadas a solventar aquellas limitaciones encontradas en la evidencia se darán de forma conjunta experimental y analíticamente con el fin de corroborar adecuadamente los resultados.
La información entregada en este artículo es una referencia útil para transmitir los avances logrados en otros países hacia aquellas regiones del mundo donde el sistema de entramado ligero de madera no ha sido mayormente divulgado.
REFERENCIAS
Lam, F., Filiatrault, A., Kawai, N., Nakajima, S. y Yamaguchi, N. (2002). Performance of timber buildings under seismic load. Part 1: Experimental studies. Progress in Structural Engineering and Materials, 4(3), 276-285. doi: https://doi. org/10.1002/pse.121
Estrella, X., Guindos, P., Almazán, J. L. y Malek, S. (2020). Efficient nonlinear modeling of strong wood frame shear walls for mid-rise buildings. Engineering Structures, 215, 110670–110670. doi: https://doi.org/10.1016/j. engstruct.2020.110670
[3] Orellana, P., Santa María, H., Almazán, J. L. y Estrella, X. (2021). Cyclic behavior of wood-frame shear walls with vertical load and bending moment for mid-rise timber buildings. Engineering Structures, 240, 112298–112298. doi: https:// doi.org/10.1016/j.engstruct.2021.112298
Bagheri, M. M. y Doudak, G. (2020). Structural characteristics of light-frame wood shear walls with various construction detailing. Engineering Structures, 205, 110093–110093. doi: https://doi.org/10.1016/j.engstruct.2019.110093
Guíñez, F., Santa María, H. y Almazán, J. L. (2019). Monotonic and cyclic behaviour of wood frame shear walls for mid- height timber buildings. Engineering Structures, 189, 100–110. doi: https://doi.org/10.1016/j.engstruct.2019.03.043
Lebeda, D. J., Gupta, R., Rosowsky, D. V. y Dolan, J. D. (2005). Effect of Hold-Down Misplacement on Strength and Stiffness of Wood Shear Walls. Practice Periodical on Structural Design and Construction, 10(2), 79–87. doi: https://doi. org/10.1061/(ASCE)1084-0680(2005)10:2(79)
Bagheri, M. M. y Doudak, G. (2021). Experimental and numerical study on the deflection of multi-storey light-frame timber shear walls. Engineering Structures, 233, 111951–111951. doi: https://doi.org/10.1016/j. engstruct.2021.111951
Salinas-Ríos, K. y Janneire García-López, A. (2022). Bibliometrics, a useful tool within the field of research Bibliometría, una herramienta útil dentro del campo de la investigación. Journal of Basic and Applied Psychology Research Biannual Publication, 3(6), 10–17. https://repository.uaeh.edu.mx/revistas/index.php/jbapr/issue/archive
Cobo, M. J., López-Herrera, A. G., Herrera-Viedma, E. y Herrera, F. (2011). Science mapping software tools: Review, analysis, and cooperative study among tools. Journal of the American Society for Information Science and Technology, 62(7), 1382–1402. doi: https://doi.org/10.1002/ASI.21525
Yepes-Nuñez, J. J., Urrútia, G., Romero-García, M. y Alonso-Fernández, S. (2021). Declaración PRISMA 2020: Una guía actualizada para la publicación de revisiones sistemáticas. Revista Española de Cardiología, 74(9), 790–799. doi: https://doi.org/10.1016/J.RECESP.2021.06.016
Saini, D. y Shafei, B. (2020). Damage assessment of wood frame shear walls subjected to lateral wind load and windborne debris impact. Journal of Wind Engineering and Industrial Aerodynamics, 198, 104091–104091. doi: https://doi.org/10.1016/j.jweia.2020.104091
Alam, M. S., Barbosa, A. R., Mugabo, I., Cox, D. T., Park, H., Lee, D. y Shin, S. (2023). Elevated light-frame wood residential building physical and numerical modeling of damage due to hurricane overland surge and waves. Engineering Structures, 294, 116774–116774. doi: https://doi.org/10.1016/j.engstruct.2023.116774
Schick, M. y Seim, W. (2019). Overstrength values for light frame timber wall elements based on reliability methods. Engineering Structures, 185, 230–242. doi: https://doi.org/10.1016/j.engstruct.2019.01.034
Pan, Y., Ventura, C. E. y Tannert, T. (2020). Damage index fragility assessment of low-rise light-frame wood buildings under long duration subduction earthquakes. Structural Safety, 84, 101940–101940. doi: https://doi.org/10.1016/j. strusafe.2020.101940
Inoue, R., Mori, T. y Matsumoto, S. (2023). Effect of numerous small deformations caused by moderate earthquakes on shear performance of wooden walls. Construction and Building Materials, 364, 130016–130016. doi: https://doi. org/10.1016/j.conbuildmat.2022.130016
Wakashima, Y., Ishikawa, K., Shimizu, H., Kitamori, A., Matsubara, D. y Tesfamariam, S. (2021). Dynamic and long-term performance of wood friction connectors for timber shear walls. Engineering Structures, 241, 112351–112351. doi: https://doi.org/10.1016/j.engstruct.2021.112351
Casagrande, D., Rossi, S., Sartori, T. y Tomasi, R. (2016). Proposal of an analytical procedure and a simplified numerical model for elastic response of single-storey timber shear-walls. Construction and Building Materials, 102, 1101–1112. doi: https://doi.org/10.1016/J.CONBUILDMAT.2014.12.114
Caprolu, G., Girhammar, U. A. y Källsner, B. (2015). Comparison of models and tests on bottom rails in timber frame shear walls experiencing uplift. Construction and Building Materials, 94, 148–163. doi: https://doi.org/10.1016/J. CONBUILDMAT.2015.05.125
Anil, Ö., Togay, A., Karagöz Işleyen, Ü., Sö ütlü, C. y Döngel, N. (2016). Hysteretic behavior of timber framed shear wall with openings. Construction and Building Materials, 116, 203–215. doi: https://doi.org/10.1016/J. CONBUILDMAT.2016.04.068
Sadeghi Marzaleh, A., Nerbano, S., Sebastiani Croce, A. y Steiger, R. (2018). OSB sheathed light-frame timber shear walls with strong anchorage subjected to vertical load, bending moment, and monotonic lateral load. Engineering Structures, 173, 787–799. doi: https://doi.org/10.1016/j.engstruct.2018.05.044
Shadravan, S. y Ramseyer, C. C. (2018). Investigation of Wood Shear Walls Subjected to Lateral Load. Structures, 16, 82–96. doi: https://doi.org/10.1016/j.istruc.2018.08.007
American Wood Council. (2015). Special design provisions for wind and seismic. American Wood Council.
Instituto Nacional de Normalización. (2009). NCh 433. Of96: Diseño Sísmico de Edificios. Norma Chilena Oficial.
Qiang, R., Zhou, L., Ni, C. y Huang, D. (2022). Seismic performance of high-capacity light wood frame shear walls with three rows of nails. Engineering Structures, 268, 114767–114767. doi: https://doi.org/10.1016/j. engstruct.2022.114767
Estrella, X., Malek, S., Almazán, J. L., Guindos, P. y Santa María, H. (2021). Experimental study of the effects of continuous rod hold-down anchorages on the cyclic response of wood frame shear walls. Engineering Structures, 230, 111641–111641. doi: https://doi.org/10.1016/j.engstruct.2020.111641
[27] Verdret, Y., Faye, C., Elachachi, S. M., Le Magorou, L. y García, P. (2015). Experimental investigation on stapled and nailed connections in light timber frame walls. Construction and Building Materials, 91, 260–273. doi: https://doi. org/10.1016/j.conbuildmat.2015.05.052
[28] European Committee for Standardization. (2004). EN1995 Eurocode 5. Design of timber structures, 144(6).
[29] American Society for Testing and Materials. (2008). ASTM E 2126: Standard test method for cyclic load test for shear resistance of vertical elements of the lateral force resisting systems for building. American Society for Testing and Materials
[30] Germano, F., Metelli, G. y Giuriani, E. (2015). Experimental results on the role of sheathing-to-frame and base connections of a European timber framed shear wall. Construction and Building Materials, 80, 315–328. doi: https:// doi.org/10.1016/j.conbuildmat.2015.01.076
[31] Zheng, W., Li, Y., Zhou, Y., Zhu, Y., Lu, W., Liu, W. y Wang, H. (2020). Experimental investigation on the behavior of plybamboo sheathing-to-framing screwed connections. Construction and Building Materials, 262, 120856–120856. doi: https://doi.org/10.1016/j.conbuildmat.2020.120856
[32] Echeverry, J. S. y Correal, J. F. (2015). Cyclic behavior of Laminated Guadua Mat sheathing-to-framing connections.
[33] Folz, B., Filiatrault, A., Project, S. S. R. y University of California, S. Diego. D. of S. E. (2000). CASHEW: A Computer Program for the Cyclic Analysis of Shear Walls. Department of Structural Engineering. University of California. https:// books.google.com.ec/books?id=jv1DAQAAIAAJ
[34] Nguyen, T. T., Dao, T. N., Aaleti, S., van de Lindt, J. W. y Fridley, K. J. (2018). Seismic assessment of a three-story wood building with an integrated CLT-lightframe system using RTHS. Engineering Structures, 167, 695–704. doi : https :// doi.org/10.1016/j.engstruct.2018.01.025
[35] Yue, K., Liang, B., Shao, Y., Xie, C., Hu, W., Zhao, M., Chen, Z. y Lu, W. (2021). Lateral behavior of wood frame shear walls sheathed with densified plywood under monotonic loading. Thin-Walled Structures, 166, 108082–108082. doi: https://doi.org/10.1016/j.tws.2021.108082
[36] Casagrande, D., Rossi, S., Tomasi, R. y Mischi, G. (2016). A predictive analytical model for the elasto-plastic behaviour of a light timber-frame shear-wall. Construction and Building Materials, 102, 1113–1126. doi: https://doi.org/10.1016/j. conbuildmat.2015.06.025
[37] Valdivieso, D., Guindos, P., Montaño, J. y Lopez-Garcia, D. (2023). Experimental investigation of multi-layered strong wood-frame shear walls with nonstructural Type X gypsum wallboard layers under cyclic load. Engineering Structures, 282, 115797–115797. doi: https://doi.org/10.1016/j.engstruct.2023.115797
[38] Humbert, J., Boudaud, C., Baroth, J., Hameury, S. y Daudeville, L. (2014). Joints and wood shear walls modelling I: Constitutive law, experimental tests and FE model under quasi-static loading. Engineering Structures, 65, 52–61. doi: https://doi.org/10.1016/j.engstruct.2014.01.047
[39] Boudaud, C., Humbert, J., Baroth, J., Hameury, S. y Daudeville, L. (2015). Joints and wood shear walls modelling II: Experimental tests and FE models under seismic loading. Engineering Structures, 101, 743–749. doi: https://doi. org/10.1016/j.engstruct.2014.10.053
[40] Peng, C., El Damatty, A. A., Musa, A. y Hamada, A. (2020). Simplified numerical approach for the lateral load analysis of light-frame wood shear wall structures. Engineering Structures, 219, 110921–110921. doi: https://doi.org/10.1016/j. engstruct.2020.110921
[41] Folz, B. y Filiatrault, A. (2001). Cyclic Analysis of Wood Shear Walls. Journal of Structural Engineering, 127(4), 433–441. doi: https://doi.org/10.1061/(ASCE)0733-9445(2001)127:4(433)
[42] Kuai, L., Ormarsson, S. y Vessby, J. (2023). Nonlinear FE-analysis and testing of light-frame timber shear walls subjected to cyclic loading. Construction and Building Materials, 362, 129646–129646. doi: https://doi.org/10.1016/j. conbuildmat.2022.129646
[43] Kuai, L., Ormarsson, S., Vessby, J. y Maharjan, R. (2022). A numerical and experimental investigation of non-linear deformation behaviours in light-frame timber walls. Engineering Structures, 252, 113599–113599. doi: https://doi. org/10.1016/J.ENGSTRUCT.2021.113599
[44] Dunton, A. y Gardoni, P. (2023). Physics-based probabilistic capacity models and fragility estimates for light wood frame shear walls. Engineering Structures, 285, 115966–115966. doi: https://doi.org/10.1016/j.engstruct.2023.115966
[45] Jensen, J. L., Caprolu, G. y Girhammar, U. A. (2016). Fracture Mechanics Models for Brittle Failure of Bottom Rails due to Uplift in Timber Frame Shear Walls. Advances in Civil Engineering, 2016. doi: https://doi.org/10.1155/2016/9402650
[46] Caprolu, G., Girhammar, U. A. y Källsner, B. (2017). Analytical models for splitting capacity of bottom rails in partially anchored timber frame shear walls based on fracture mechanics. Wood Material Science & Engineering, 12(3), 165–
[47] Caprolu, G., Girhammar, U. A., Källsner, B. y Lidelöw, H. (2014). Splitting capacity of bottom rail in partially anchored timber frame shear walls with single-sided sheathing. The IES Journal Part A: Civil & Structural Engineering, 7(2), 83–105. doi: https://doi.org/10.1080/19373260.2014.898558
[48] Caprolu, G., Girhammar, U. A. y Källsner, B. (2015). Splitting capacity of bottom rails in partially anchored timber frame shear walls with double-sided sheathing. The IES Journal Part A: Civil & Structural Engineering, 8(1), 1–23. doi: https:// doi.org/10.1080/19373260.2014.952607
[49] Estrella, X., Guindos, P., Almazán, J. L., Malek, S., Santa María, H., Montaño, J. y Berwart, S. (2021). Seismic performance factors for timber buildings with woodframe shear walls. Engineering Structures, 248, 113185–113185. doi: https:// doi.org/10.1016/j.engstruct.2021.113185
[50] Berwart, S., Estrella, X., Montaño, J., Santa-María, H., Almazán, J. L. y Guindos, P. (2022). A simplified approach to assess the technical prefeasibility of multistory wood-frame buildings in high seismic zones. Engineering Structures, 257, 114035–114035. doi: https://doi.org/10.1016/j.engstruct.2022.114035