1 Introducción

Sea Λ un álgebra de artin y Λ mod la categoría de Λ módulos izquierdos finitamente generados. Dado un Λ-módulo proyectivo .. , denotemos por . mod la subcategoría plena de Λ mod formada por los Λ módulos .. que admiten presentaciones de la forma

donde .., P., son sumas de sumandos directos de . . Sea Γ = End.(. )op, la opuesta del álgebra de endomorfismos de . . El teorema de proyectivización de Auslander (ver [2, I, (2.1), (2.5), y (Ejercicio 2)] establece que las categorías . −mod y Γ−mod son equivalentes mediante los funtores Hom.(P, −) y . ⊗. −: Hom.(P, −) : . −mod --Γ−mod : . ⊗. −.

Sin embargo, en general no hay relación entre las dimensiones homológicas de las categorías Λ−mod y Γ−mod.

En este trabajo consideramos el caso particular en que . = . . es la suma directa un representante de ca- da clase de isomorfismo de los Λ módulos proyecti- vos indescomponibles . tales que el cociente de . por su radical es un módulo simple de dimensión proyectiva infinita. En particular mostramos que si . es un Λ módulo tal que la dimensión proyectiva del Γ módulo Hom.(. .,M ) es finita, entonces se tiene que la dimensión proyectiva de . también lo es. Como con- secuencia, si es que Λ tiene dimensión global infinita, todos los Γ módulos simples tienen dimensión proyectiva infinita.

El artículo está estructurado de la siguiente manera: en la sección 2, sección de preliminares, hacemos un breve recuento de notaciones, construcciones y resultados necesarios para los resultados principales, que serán expuestos en la sección 3, en donde además daremos algunos ejemplos.

2 Preliminares

Si bien recordamos algunas nociones y notaciones, refe- rimos al lector a [1, 2], por ejemplo, para mayores deta- lles de álgebra homológica y teoría de representaciones de álgebras.

En todo este trabajo Λ designará un álgebra de artin, cuyo radical de Jacobson será r. El radical de la categoría Λ−mod es el ideal r. = r(Λ−mod) de ésta últi- ma definido, para cada par X, Y de Λ−módulos, mediante r.(X, Y ) = {. ∈ Hom.(X, Y )| hfg no es un isomorfismo para ningunos . ∈ Hom.(U, X), y . ∈

Dado un Λ módulo . , su dimensión proyectiva será denotada por dpΛ . , y su top es top M = M.rM. Ade- más, add . denotará la subcategoría plena de Λ mod formada por los módulos que son sumas de sumandos directos de . .

La dimensión finitística de Λ es:

fin dim Λ = sup{dpΛ .| . ∈ Λ−mod, dpΛ X < ∞},

y su dimensión global es

dim gl Λ = sup{dpΛ .| . ∈ Λ−mod}.

El siguiente resultado, bien conocido (ver por ejemplo [1, X, 1.4]), nos será de utilidad más adelante.

Lema 2.1 Si se tiene una sucesión exacta corta en Λ−mod

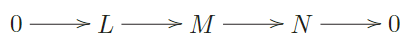
Entonces:

a) dpΛ . sup{dpΛ M, dpΛ . + 1}, y se da la igualdad si y solamente si es que dpΛ . /= dpΛ

b) dpΛ . sup{dpΛ M, dpΛ . −1} y se da la igual- dad si y solamente si es que dpΛ . /= dpΛ N .

c) dpΛ . sup{dpΛ L, dpΛ . } y se da la igualdad

Denotaremos por .. a la suma directa de los Λ−módulos a la suma directa de losΛ−módulossimples de dimensión proyectiva infinita (uno por cadaclase de isomorfismo). De este modo, P∞es la cober-tura proyectiva de ..

De manera análoga, S^<. denotará a la suma directa de los módulos simples de dimensión proyectiva finita (uno por cada clase de isomorfismo). Además, definamos .. mediante:

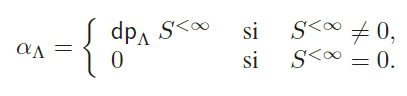
Finalmente el índice de . en .., [. : ..], es el número de factores de composición (no necesariamente distintos) de . cuya dimensión proyectiva es infinita. El índice [. : S^<.] se define de manera análoga. Es inmediato entonces observar los siguientes hechos, que usaremos libremente en adelante (ver también el Lema (2.3)):

Observación 2.2 Dado un Λ−módulo M , entonces:

a) [. : ..] = 0 implica que dpΛ . ..

b) [. : ..] = 0 si, y solamente si es que Hom.(. .,M ) = 0

Dada una subcategoríaF⊆Λ−mod, diremos que unΛ−móduloMes filtrado porFsi es que existe una ca-dena finita de submódulos deM:

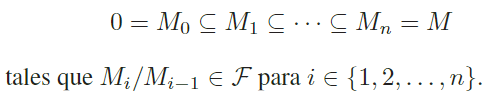
Recordemos ahora la construcción del funtor

S:Λ−modΛ−mod de [3].

EnΛ−modla relación definida porC1C2 si y solamente si es que existe un epimorfismo C1C2 es una relación de orden. El Lema (3.3) de [3] establece que, dado unΛ−módulo M, la familia de cocientes de M filtrados por S<∞admite un único elementomaximal, que denotamos porC(M). Notemos que porconstrucción se tiene[C(M):S∞]=0.

Dado que C(M)es un cociente deM, existe un epimorfismo pM:MC(M). Por definición, S(M)es el núcleo de pM. Esto define S en los objetos deΛ−mod.

Por otro lado, para un morfismo f:MN, tenemos que pN f(M)es un cociente de M contenido en C(N), que es filtrado por S<∞

De este modo obtenemos la existencia de un epimorfis- mo C(. ) : C(. )----------------------------- p. f (. ), lo que, por paso al núcleo proporciona un morfismo S(. ) : S(. ) S(. ).

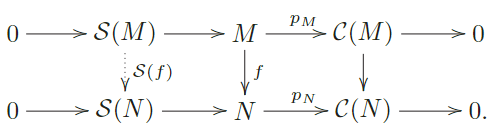
El siguiente Lema ([3, 3.4]) resume algunas propieda- des del funtor S que utilizaremos más adelante.

Lema 2.3 : Λ mod ----Λ mod es un funtor adi- tivo que tiene las siguientes propiedades:

a) Si [. : ..] = 0, entonces top S(M) ∈ add S∞,

b) dpΛ . sup{dpΛ S(. ), α.},

c) . preserva los epimorfismos y los monomorfismos,

d) Si [. : ..] = 0 entonces S(. ) = 0.

3 Resultados

Dado .. . . mod, el resultado de Auslander mencionado en la introducción garantiza que

. . ⊗. Hom.(. ., M.) ~ ...

Si . es un Λ módulo arbitrario, esto no es cierto. Sin embargo Hom.(. .,M ) sigue siendo un Γ módulo, de modo que, de nuevo gracias al resultado de Auslan- der, debe existir un Λ−módulo . . ∈ . .−mod tal que

Hom.(. .,M ) ~ Hom.(. .,M .).

Consecuentemente tendremos entonces

. . ⊗. Hom.(. .,M ) ~ . . ⊗. Hom.(. .,M .)

~ . ..

En lo que sigue construiremos concretamente el módulo . ., y veremos que además tiene algunas propiedades adicionales:

Proposición 3.1 Dado un Λ−módulo M , existe M . ∈. .−mod, tal que

∞

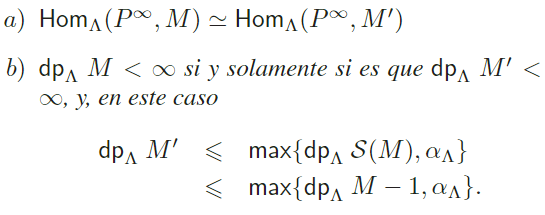
Demostración: La demostración de .) es la discusión que precede el enunciado de la Proposición. El enunciado de .) seguirá de la construcción de . . y del Lema (2.1). Tenemos dos casos distintos a tratar, según [. : ..] sea cero o no.

Supongamos primero que [. : ..] = 0, es decir que . no tiene factores de composición de dimensión proyectiva infinita. En virtud de la Observación (2.2), tenemos que

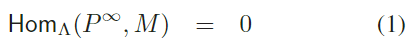[1]

con lo que podemos tomar . . = 0 y no hay nada que demostrar.

Podemos entonces suponer que [. : ..] = 0. Consi- deremos la sucesión exacta corta

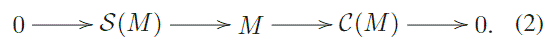[2]

Como (. ) es filtrado por S^<., tenemos que [ (. ) : ..] = 0. En virtud de la exactitud de Hom.(. ., ) y la Observación (2.2), tenemos entonces

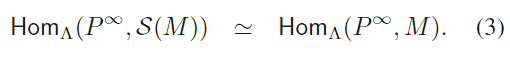[3]

Además el Lema (2.3), parte .), da que la cobertura pro- yectiva de (. ), que llamaremos .., está en add . .. Tenemos entonces un diagrama cuya línea y columna son exactas:

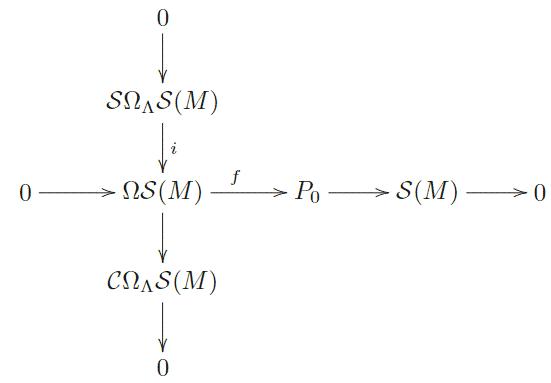
Sea . . = Coker f i, j obtenido de . por paso a los conúcleos, y . = Ker .. El lema de la serpiente nos da un diagrama conmutativo con líneas y columnas exactas:

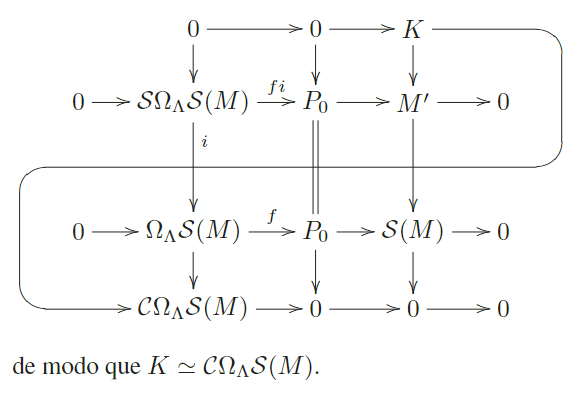
Al aplicar el funtor Hom.(. ., −) se obtiene otro dia- grama conmutativo de líneas exactas. El hecho que [CΩ. S(. ) : ..] = 0, nos dice que:

Supongamos que [Ω. . : ..] = 0. Esto implica que top Ω. (M) add S∞, de nuevo gracias al Lema (2.3). Esto a su vez implica que la cobertura proyectiva de Ω. (. ) está en add . .. Como también es el caso para .., tenemos efectivamente . . . . mod, tal como queríamos. El Lema (2.3), parte .) y la sucesión exacta (2) dan que dpΛ M < si y solamente si dpΛ (. ) < . Además, como . Ω. (. ), te- nemos, gracias a la Observación 2.2, .), que dpΛ . ,( .. Así, gracias el Lema (2.1), aplicado a la tercera columna del diagrama precedente, nos dice que dpΛ (. ) < si y solo si es que dpΛ . . < . Las desigualdades deseadas siguen del Lema (2.1).

Si, al contrario, tenemos que [Ω . : ..] = 0 te- nemos, por el enunciado .) de la Observación 2.2, que Hom.(. ., Ω.S(. )) = 0, lo que implica que

Hom.(. ., P.) ~ Hom.(. ., S(. ))

~ Hom.(. .,M )

con lo que .. es el módulo . . que buscábamos.

Observación 3.2 Las sucesiones exactas en P . mod no necesariamente son exactas en Λ mod, incluso si la primera es una subcategoría plena de la segunda. Es más, el funtor P .⊗. : Γ−mod --. .−mod es exacto, pero el funtor P . . : Γ mod no.

Proposición 3.3 Sea M ∈ Λ−mod, entonces:

a) Si P. es la cobertura proyectiva de (. ), Hom.(. ., P.) es la cobertura proyectiva de Hom.(. .,M ) en Γ−mod.

b) Ω.Hom.(. .,M ) ~ Hom.(. ., (Ω.S)nM ).

Demostración: a) Notemos primero que, de nuevo, si[M, S∞]=0, tendríamos, por la Observación (2.2),parte b) que HomΛ(P∞,M)=0; y por el Lema (2.3),partee),S(M)=0, con lo que no habría nada que demostrar.

Sin pérdida de generalidad podemos entonces suponer que [M, S.] /= 0. Recordemos además que la Ecuación (3) nos dice que Hom.(. .,M ) ~ Hom.(. ., S(. )).

Sea . : .. --(. ) la cobertura proyectiva de (. ). Tenemos entonces una sucesión exacta corta:

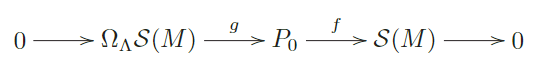
Aplicando el funtor Hom.(. ., ) obtenemos una su- cesión exacta corta

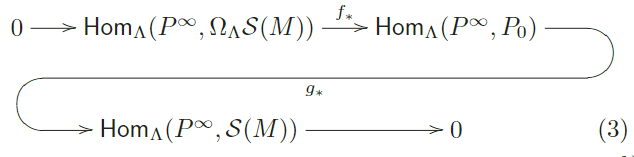
Donde .. = Hom.(. .,f), y .. = Hom.(. ., g).

Como vimos en la demostración de la Proposición (3.1), .. add . ., de modo que Hom.(. ., P.) es un Γ módulo proyectivo. Para demostrar que Hom.(. ., g) es una cobertura proyectiva, debemos demostrar que es un morfismo superfluo ([1, VIII, (2.1)]), o, de manera equivalente, que Ker Hom.(. ., g), está contenido en el radical de Hom.(. ., P.). Dada la exactitud de la sucesión precedente, esto es equivalente a mostrar que Hom.(. .,f) está en r..

Supongamos que no es el caso. Dado que los Γ módulos proyectivos son de la forma Hom.(. .,P .) con . .add . . esto equivale a suponer que existe un factor directo indescomponible .0I de .. tal que la composición de . con la proyección canónica . de . . en .0I

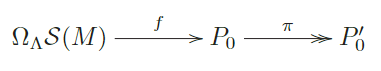
Induce un morfismo:

HomΛ(P∞,πf):HomΛ(P∞,P0)HomΛ(P∞,P′0)que no está enrΓ. Como HomΛ(P∞,P′0)es proyectivo indescomponible, tenemos que HomΛ(P∞,πf)es una retracción con lo que todo morfismoP∞P′0sefactoriza porπf. PeroP′0es factor directo deP∞, así que tenemos una proyección canónicap:P∞P′0.Decir que ésta se factoriza por π f implica que π f no está en rΛ lo que contradice el hecho que f si está en rΛ. b)Paran=0no hay nada que probar, y paran=1, el resultado sigue inmediatamente de la partea)y la sucesión(3). Paran2se procede por inducción obvia.

Proposición 3.4 Sea M ∈ Λ−mod. Entonces:

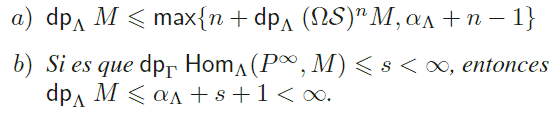
Demostración: a) Por el Lema (2.1) tenemos que

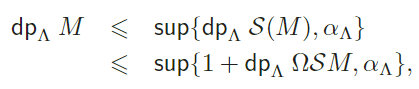
de modo que el enunciado es verdadero para n = 1. Supongamos ahora que la desigualdad se cumple para . − 1 ) 1. Tenemos entonces:

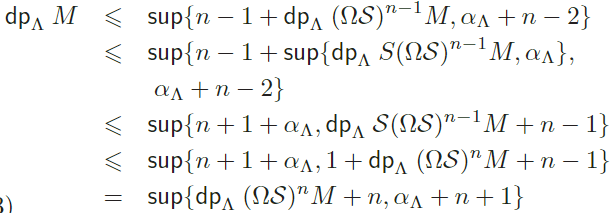
b) Supongamos que dpΓ HomΛ(P ∞,M ) s < , de modo que Ω.⁺¹Hom.(. .,M ) = 0, así que en virtud de la Proposición (3.3) tenemos que

Hom.(. ., (ΩS).+1(. ))=0

lo que implica que dpΛ (Ω )s+1M αΛ. Por la parte a) tenemos entonces que

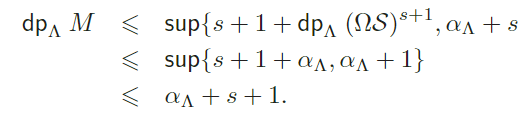
Corolario 3.5 Para todo Γ−módulo simple .S se tiene dpΓ . = ∞.

Demostración: Es claro que .. ~ Hom.(. ., ...) para algún Λ−módulo simple . que es factor directo de .., de modo que dpΛ .. = ∞. Por el resultado precedente se tiene que dpΓ . = ∞.

Notemos que el corolario precedente es válido solamente en el caso en que . . es la suma directa de todos los Λ módulos proyectivos indescomponibles cuyo top tiene dimensión global infinita. El siguiente ejemplo muestra que al dejar de lado alguno de estos proyectivos, se puede obtener un álgebra de dimensión global arbitraria.

Ejemplo 3.6 Sean . un cuerpo, .. el ciclo orienta caminos de longitud dos y Λ = kA./I. Tenemos que dpΛ S. = ∞ para i ∈ {1,..., n}.

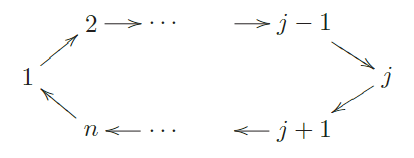
Si tomamos P = .. ⊕ · · · ⊕ P.₋₁, entonces Γ =End.(. )op ~ kA.₋₁/J (donde J es el ideal generado por los caminos de longitud dos) es un álgebra triangu- lar tal que dim gl Γ= dpΓ Hom.(. ., S.₋₁)= . – 2.

Observación 3.7 En la Proposición (2.1) mostramos que si es que dpΓ Hom.(. .,M ) s, entonces dpΛ . .. + . + 1. En el otro sentido, si pudiésemos encontrar una constante β tal que dpΛ . s implica dpΓ Hom.(. .,M ) . + β, tendríamos

fin dim Λ < ∞ ⇐⇒ fin dim Γ < ∞.

En efecto, supongamos que tenemos una tal constan- te β y que fin dim Λ < . Sea X Γ mod con dpΓ X < s. Como X = Hom.(. .,M . para algún M P . mod con dpΛ . fin dim Λ, tendríamos entonces

dpΓ . = dpΓ Hom.(. .,M ) fin dim Λ+ .

La otra implicación se muestra de la misma manera.

Desafortunadamente, no es posible obtener una tal cons- tante ., como el siguiente ejemplo muestra:

Ejemplo 3.8 Sea Q el carcaj

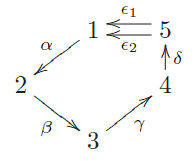
Consideremos el ideal I .< αβγ, βγδ&., βγδ&., δ&., γδ&.αβ, &.αβ >, y sea Λ= kQ/I. Un cálculo directo muestra que dpΛ .. = dpΛ .. = dpΛ .. = dpΛ .. =

, y dpΛ .. = 3, de modo que P . = .. ..

.. ..,y α. = 3. Si, como antes, denotamos por . al álgebra End.(. .)op, tenemos que dpΛ .. = 0, pero dpΓ Hom.(. ., P.)= ∞.

Terminemos determinando el Λ−módulo M . tal que

. . ⊗. Hom.(. ., P.) ~ . ..

Notemos que P. =2 . De acuerdo a la construcción de la Proposición (3.1) tenemos:

El módulo 2 tiene dimensión proyectiva .. En efecto, su resolución proyectiva es:

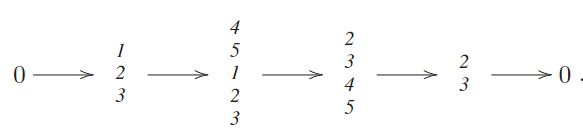
Referencias bibliográficas

[1] . Assem. Algèbres et modules: cours et exerci- ces. Enseignement des mathématiques. Les Presses de l’Université d’Ottawa–Masson, Ottawa–Paris, 1997.

[2] M. Auslander, I. Reiten, and S.O. Smalø. Repre- sentation Theory of Artin Algebras. Number 36 in Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge, 1995.

[3] F. Huard, M. Lanzilotta, and O. Mendoza. Finitis- tic dimension through inifnite projective dimension. preprint, 2007.