About this paper

The present article was published on April 13th, 2023 in the European Journal of Applied Sciences and it has been assigned a DOI by the EJAS. The work is republished by ACIAvances en Ciencias e Ingenierías according to the creative commons license (Attribution4.0 International, CC BY 4.0) used by the EJAS, and according to the copyright preserved by the author, Bruce Hoeneisen. Readers can access the original publication via the following link: https://journals.scholarpublishing.org/index.php/AIVP/article/view/14383 or through the DOI: https://doi.org/10.14738/aivp.112.14383.

INTRODUCTION

Most of the matter in the universe, 84.3 ± 0.2 % [1], is in a “dark matter” form that has been “observed” only through its gravitational interaction. As far as we know, this dark matter does not have any other interaction, at least down to the current sensitivity of our experiments and observations. Fritz Zwicky in 1933 found that the matter in the Coma cluster of galaxies greatly exceeds the mass in stars [2]. According to the book by Stefano Profumo [3], the mass m_h of dark matter particles is unknown over 90 orders of magnitude! In summary, we know exactly how much dark matter there is,but do not have the foggiest idea what it is.

This article presents an overview of a data driven solution to the dark matter problem.

MEASUREMENTS

Let us assume that dark matter is a gas of particles that is ultra-relativistic in the early universe. As the universe expands, dark matter cools, and becomes non-relativistic. We expect that this non-relativistic gas is classical, i.e. has negative chemical potential [4] [5]. Let V_hrms (a) be the root-mean-square velocity of the non-relativistic dark matter particles. a(t) is the expansion parameter of the universe at time t, normalized to a(t₀) = 1 at the present time.²V²_hrms (a) is proportional to the dark matter temperature-to-mass ratio. As the universe expands, dark matter cools, V_hrms (a) varies in proportion to 1/a [6], and the dark matter density p_h (a) varies in proportion to 1/a³ , so

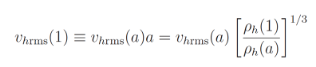(1)

does not depend on . In other words, we say that V_hrms(1) is an “adiabatic invariant”.

It turns out that, to unravel the dark matter mystery, we need to measure the adiabaticinvariant V_hrms(1), and the related observable kfs = 2π/λfs, that we now explain. Due to the velocity dispersion V_hrms (a), dark matter particles free-stream in and out of density minimums and maximums, erasing primordial density fluctuations of “comoving” wavelength less than approximately λ_fs [4] [7]. (Since wavelengths growin proportion to a(t), it is customary to refer the wavelength to the present time, i.e. a(t₀) = 1, hence the word “comoving”.) k_fs is the comoving cut-off wavenumber due to dark matter free-streaming. The theoretical relation between the two observables, V_hrms(1) and k_fs, is summarized in Table 1 [4] [7].

To measure k_fs we compare observed and predicted galaxy rest-frame ultra-violetluminosity distributions, and observed and predicted galaxy stellar mass distributions.An example, corresponding to “redshift” z = 6, or equivalently, expansion parameter a = 1/(1+z) = 1/7, is shown in Figure 1. Note that warm dark matter free-streaming attenuates small scale fluctuations and therefore reduces the numbers of galaxies with low mass. From this, and similar figures at redshifts z = 4, 8 and 10, we obtain k_fs = 2.0^+0.8_−0.5 Mpc⁻¹ [17].

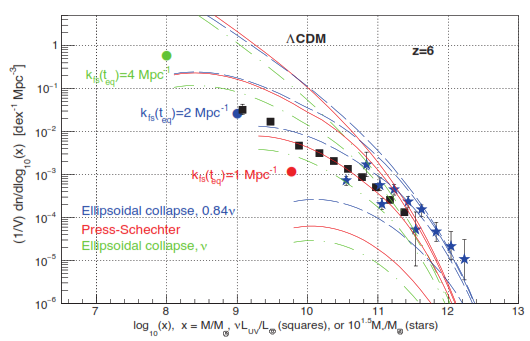
Figure 1.

Shown are distributions of x, where x is the observed galaxy stellar mass M_*/M_. times 10^1.5 (stars) [8] [9] [10], or the observed galaxy UV luminosity vL_UV/L_. (squares) [11] [12] [13] (corrected for dust extinction [14] [15]), or the predicted linear total (dark matter plus baryon) mass M/M_. (lines), at redshift z = 6. The symbol . means “sun”. The Press-Schechter prediction, and its Sheth-Tormen ellipsoidal collapse extensions, correspond, from top to bottom, to the warm dark matter free-streaming cut-off wavenumbers k_fs = 1000, 4, 2 and 1 Mpc⁻¹. The round red, blue and green dots indicate the velocity dispersion cut-offs of the predictions [16] at k_fs = 1, 2 and 4 Mpc⁻¹, respectively. Presenting three predictions illustrates the uncertainty of the predictions. Note that the data agree with predictions for k_fs = 2 Mpc⁻¹.

Table 1.

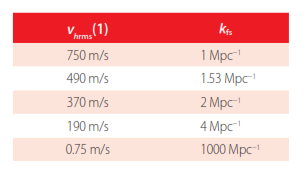
Calculated relation between the adiabatic invariant V_hrms(1), and the comoving cut-off wavenumber k_fs, due to dark matter free-streaming [4] [7]. “Mega-parsec” (Mpc) is a unit of length used in cosmology.

To measure the adiabatic invariant V_hrms(1) we note the following. Consider a free observer in a density peak in the early universe. This observer “sees” dark matter expand adiabatically, i.e. conserving V_hrms(1), due to the expansion of the universe, reach maximum expansion, followed by adiabatic compression into the core of the galaxy due to gravitational attraction. The core of the galaxy forms adiabatically if dark matter is warmas we have assumed, i.e if V_hrms(1) is greater than zero [18]. Rotation and relaxation, due to galaxy collisions and mergers, increase the observed V'_hrms(1) above the true V_hrms(1) [6]. So, as long as rotation and relaxation remain negligible, we predict that the adiabatic invariant in the core of the galaxy is the same as in the early universe, and so should be thesame for all galaxies (with negligible rotation and relaxation). The adiabatic invariant in thecore of a spiral galaxy can be obtained from the observed rotation curves of neutral atomic hydrogen gas or of stars, together with infrared and visible images [19]. The distribution ofthe adiabatic invariant measured in several dwarf galaxies is shown in Figure 2. We obtain anarrow peak with V_hrms(1) = 406 ± 69 m/s [6]. The few galaxies with V'_hrms(1) to the right of this peak have significant rotation and/or relaxation.

We note, from Table 1, that the measurements of k_fs and V_hrms(1) are consistent with each other. We conclude that, 1) V_hrms (1) in the core of galaxies (corrected for dark matter rotation and relaxation) is of cosmological origin, as inferred form the narrowness of the peak in Figure 2, and as predicted for warm dark matter [18] [21]; and 2) that k_fs is indeed due to warm dark matter particle free-streaming. Additional observables studied, thatobtain consistent results, are the redshift of first galaxies [16], the ultra-violet luminosityof first galaxies [17], and the related “reionization optical depth” [17]. For a summary ofmeasurements see [17].

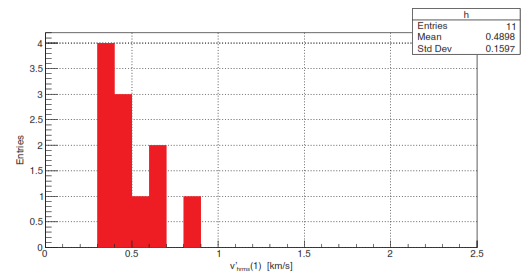
Figure 2

Distribution of V'_hrms(1), i.e. the adiabatic invariant before the dark matter rotation and relaxation correction, of 11 dwarf galaxies. These corrections can only be negative, and so are negligible in the peak at V'_hrms(1) ≈ V_hrms (1) ≈ 0.4 km/s. Data from [20].

These measurements obtain the dark matter temperature-to-mass ratio, not separately the temperature or mass. At this point we have already learned something: dark matter models that predict V_hrms(1) in disagreement with these measurements can be ruled out (if the measurements are correct). In particular, cold dark matter candidates, such as “WIMPS” and “axions”, are disfavored. Let us mention that the entire analysis is data driven,with full details, and the sources of all data and measurements, available in the references.

COLD AND WARM DARK MATTER

The cold dark matter ΛCDM theory, with only six parameters, is in spectacular agreement with the large scale phenomena of the “Cosmic Microwave Background Radiation”, “Baryon Acoustic Oscillations”, and the large scale matter distribution of the universe. However, there are, or appear to be, tensions with small scale phenomena, less than the size of the Galaxy, known as the “Core-Cusp Problem”, the “Missing Satellites Problem”, and the rest frame ultra-violet luminosity cut-off required to not exceed the “Reionization Optical Depth” measured by the Planck collaboration. Adding to the cold dark matter ΛCDM theory one more parameter, namely the adiabatic invariant V_hrms(1), obtains the warm dark matter ΛWDM cosmology. It turns out that ΛWDM agrees with ΛCDM on large scales, and, with the measured V_hrms(1) and k_fs indicated above, solves all of the mentioned small scale tensions [18] [22].

NO FREEZE-IN AND NO FREEZE-OUT

And now comes the miracle. The measured k_fs and V_hrms(1), or equivalently, the measured dark matter temperature-to-mass ratio, happen to coincide with the predictions of the“no freeze-in and no freeze-out” scenario of spin zero dark matter particles that decoupleearly on from the Standard Model sector, e.g. dark matter particles coupled to the Higgsboson, or to the top quark. Let me explain. “No freeze-in” means that dark matter reachesthermal and diffusive, i.e. chemical, equilibrium, in the early universe, with the particles ofthe “Standard Model of Quarks and Leptons”, or, loosely speaking, with ordinary matter. Dark matter then decouples from the Standard Model sector while still ultra-relativistic. “Nofreeze-out” means that, when dark matter becomes non-relativistic, its mutual interactionsare so weak that these particles do not annihilate each other. An example of spin zero darkmatter coupled to the Higgs boson is shown in Figure 3.

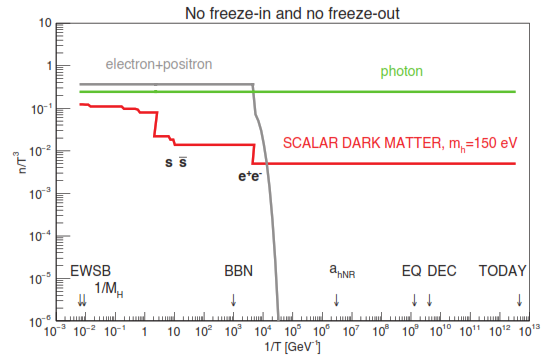
Figure 3.

The “no freeze-in and no freeze-out” warm dark matter scenario is illustrated for spin zero warm dark matter particles coupled to the Higgs boson. T is the photon temperature, and the n’s are particle numberdensities, i.e. numbers of particles per unit volume. The abreviations stand for “Electro-Weak Symmetry Breaking”,“Big Bang Nucleosynthesis”, “EQuivalence” of matter and radiation densities, and “DECoupling” of photons fromStandard Model matter. Dark matter particles become non-relativistic at a_hNR. Time advances towards the right.

If dark matter is created by Higgs boson annihilation or decay, then freeze-in and/or freeze out lowers the dark matter temperature-to-mass ratio. In this case, the measured V_hrms(1) is evidence of no freeze-in and no freeze-out, not a coincidence.

If spin zero dark matter is indeed coupled to the Higgs boson [23], then the no freeze in and no freeze-out scenario, together with the measured dark matter density and measured cosmic microwave background temperature, predicts V_hrms(1) = 490 ± 10 m/s, k_fs = 1.53 ± 0.03 Mpc⁻¹, and the mass of the dark matter particles m_h = 150±2 eV [4], or about 1/3400 of the electron mass. See the Appendix for details of the calculations.³ For couplings to other massive Standard Model particles, the predictions vary slightly. The data disfavors spin one-half and spin one dark matter coupling to Standard Model particles, since their predicted V_hrms(1) is greater than observations [17].

The minimal extension of the Standard Model to obtain the no freeze-in and no freeze out scenario of dark matter is to add a real scalar field S with Z₂ symmetry S ↔ -S that couples to the Higgs boson Φ as L_SΦ = -1/2 λ_hS (Φ⁺ Φ) S² [23]. The fields Φ [25] and/or S can be the “inflaton” that drives inflation. For example, for a reheating temperature T ≈ 10¹⁵ GeV, equilibrium between Φ and S is obtained with λ_hS≳10⁻⁷.

CONCLUSIONS

In summary, we redundantly measure the dark matter temperature-to-mass ratio, and arrive at a plausible, data driven, and detailed solution to the dark matter problem, i.e. the no freeze-in and no freeze-out scenario of scalar dark matter that decouples early on from the Standard Model sector.

ACKNOWLEDGEMENT

I thank Kirk McDonald for critically reviewing this article and several of the references.

REFERENCES

[1] Particle Data Group et. al. (2020). Review of Particle Physics. Progress of Theoretical and Experimental Physics, 2020 (8). doi: https://doi.org/10.1093/ptep/ptaa104

[2] Zwicky, F. (1937). On the masses of nebulae and of clusters of nebulae. Astrophys. J., 86, 217. doi: http://dx.doi.org/10.1086/143864

[3] Profumo, S. (2017). An introduction to particle dark matter. World Scientific. doi: https://doi.org/10.1142/q0001

[4] Hoeneisen, B. (2022a). Comments on warm dark matter measurements and limits. International Journal of Astronomy and Astrophysics, 12, 94–109. doi: https://doi.org/10.4236/ijaa.2022.121006

[5] Paduroiu, S., Revaz, Y. and Pfenniger, D. (2015). Structure formation in warm dark matter cosmologies top-bottom upside-down. https://arxiv.org/pdf/1506.03789.pdf

[6] Hoeneisen, B. (2022b). Measurement of the dark matter velocity dispersion with dwarf galaxy rotation curves. International Journal of Astronomy and Astrophysics, 12, 363–381. doi: https://doi.org/10.4236/ijaa.2022.124021

[7] Boyanovsky,D., deVega, H. and Sanchez, N. (2008).The dark matter transfer function: Free streaming, particle statistics and memory of gravitational clustering. Physical Review D,78(6).doi:https://doi.org/10.1103\%2Fphysrevd.78.063546

[8] Song, M., Finkelstein, S. L., Ashby, M. L. N. et al. (2016). The evolution of the galaxy stellar mass function at z = 4 - 8: A steepening low-mass-end slope with increasing redshift. ApJ, 825, 5. doi: https://doi.org/10.48550/arXiv.1507.05636

[9] Grazian, A., Fontana, A., Santini, P. et al. (2015). The galaxy stellar mass function at 3.5 ≤ z ≤ 7.5 in the candels/ uds, goods-south, and hudf fields. Astronomy and Astrophysics, 575, A96. doi: https://doi.org/10.1051/0004-6361/201424750

[10] Davidzon, I., Ilbert, O., Laigle, C. et al. (2017). The cosmos2015 galaxy stellar mass function: 13 billion years of stellar mass assembly in 10 snapshots. Astronomy and Astrophysics, 605. doi: https://doi.org/10.1051/0004-6361/201730419

[11] Bouwens, R. and et al. (2015). Uv luminosity functions at redshifts z ≈ 4 to z ≈ 10:10000 galaxies from hst legacy fields. The Astrophysical Journal, 803, 34. doi: https://doi.org/10.1088/0004-637X/803/1/34

[12] Bouwens, R. and et al. (2021). New determinations of the uv luminosity functionsfrom z ≈ 9 to z ≈ 2 show a remarkable consistency with halo growth and a constant star formation efficiency. The Astronomical Journal, 162 (2). doi: https://doi.org/10.3847/1538-3881/abf83e

[13] McLeod, D. and et al. (2015). New redshift z ≈ 9 galaxies in the hubble frontier fields: Implications for early evolution of the uv luminosity density. MNRAS, 450 (3), 3032. doi: https://doi.org/10.1093/mnras/stv780

[14] Lapi, A. and Danese, L. (2015). Cold or warm? constraining dark matter with primeval galaxies and cosmic reionization after planck. Journal of Cosmology and Astroparticle Physics, 2015. doi: https://doi.org/10.1088/1475-7516/2015/09/003

[15] Bouwens, R., Illingworth, G. and Oesch, P. (2014). Uv-continuum slopes of 4000 z ≈ 4−8 galaxies from the hudf/ xdf, hudf09, ers, candels-south, and candels-north fields. ApJ, 793, 115. doi: https://doi.org/10.1088/0004-637X/793/2/115

[16] Hoeneisen, B. (2022c). Warm dark matter and the formation of first galaxies. Journal of Modern Physics, 13, 932–948. doi: https://doi.org/10.4236/jmp.2022.136053

[17] Hoeneisen, B. (2022d). Measurement of the dark matter velocity dispersion with galaxy stellar masses, uv luminosities, and reionization. International Journal of Astronomy and Astrophysics, 12, 258–272. doi: https://doi.org/10.4236/ijaa.2022.123015

[18] Hoeneisen, B. (2022e). Warm dark matter and the formation of first galaxies. Journal of Modern Physics, 13, 932–948. doi: https://doi.org/10.4236/jmp.2022.136053

[19] Hoeneisen, B. (2019a). The adiabatic invariant of dark matter in spiral galaxies. International Journal of Astronomy and Astrophysics, 9, 355–367. doi: https://doi.org/10.4236/ijaa.2019.94025

[20] Oh, S. and et al. (2015). High-resolution mass models of dwarf galaxies from little things. The Astronomical Journal, 149, 180. doi: https://doi.org/10.1088/0004-6256/149/6/180

[21] Hoeneisen, B. (2019b). A study of dark matter with spiral galaxy rotation curves. International Journal of Astronomy and Astrophysics, 9, 71–96. doi: https://doi.org/10.4236/ijaa.2019.92007

[22] Hoeneisen, B. (2023). A study of warm dark matter, the missing satellites problem, and the uv luminosity cut-off. International Journal of Astronomy and Astrophysics,13, 25–38. doi: https://doi.org/10.4236/ijaa.2023.131002

[23] Hoeneisen, B. (2021). Adding dark matter to the standard model. International Journal of Astronomy and Astrophysics, 11, 59–72. doi: https://doi.org/10.4236/ijaa.2021.111004

[24] Hoeneisen, B. (2020).What is dark matter made of? [Presentado at the 3rd World Summit on Exploring the Dark Side of the Universe Guadeloupe Islands, March 9-132020]. https://inspirehep.net/files/7cfb2bf406baf315315e389e6eff3809

[25] Bezrukov, F., Magnin, A., Shaposhnikov, M. and Sibiryakov, S. (2011). Higgs inflation: Consistency and generalisations. JHEP, 01, 016. doi: https://doi.org/10.1007/JHEP01(2011)016

APPENDIX A: THE NO FREEZE-IN AND NO FREEZE-OUT SCENARIO

We present a summary of Section 3 of [4] to make the present article self-contained.

We assume that the ultra-relativistic dark matter is in thermal and diffusive equilibrium with the Standard Model sector in the early universe. In particular we assume that the ultra-relativistic dark matter has zero chemical potential. We assume that dark matter decouples from the Standard Model sector while still ultra-relativistic. As the universe expands, dark matter cools and becomes non-relativistic. We assume that the ultra- relativistic Bose-Einstein or Fermi-Dirac momentum distribution of dark matter relaxes to the corresponding non-relativistic distribution, as justified in [5], thereby acquiring a negative chemical potential [5].

Let T_h/T be the dark matter-to-photon temperature ratio after decoupling of neutrinos, and after e⁺e^- annihilation, and before dark matter becomes non-relativistic. This ratio is [5] [4]

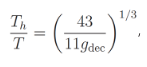(2)

where 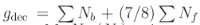at decoupling of dark matter from the Standard Model sector [1]. Nf (Nb) is the number of fermion (boson) spin polarizations. The ratio of number densities of dark matter particles and photons, after e⁺e^- annihilation until the present time, is [5] [4]

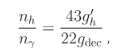(3)

where 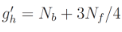for the dark matter [5]. Then, at the present time,

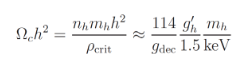(4)

determines the dark matter particle mass m_h corresponding to no freeze-in and no freeze-out.

For bosons, from equation (26) of [5], we obtain

(5)

(6)

For bosons, from equation (28) of [5], we obtain

(7)

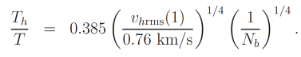(8)

Note that the measurement of the adiabatic invariant V_hrms(1) allows a determination of the dark matter particle mass m_h, and of the ratio T_h/T (that determines the dark matter decoupling temperature, if sufficiently precise).

Notes