



Sección A: Ciencias Exactas y Físicas
Edad del universo y la densidad de energía de la radiación
Age of the universe and the energy density of radiation
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
ISSN: 1390-5384
ISSN-e: 2528-7788
Periodicidad: Bianual
vol. 7, núm. 2, 2014
Recepción: 22 Octubre 2015
Aprobación: 01 Noviembre 2015
Publicación: 30 Diciembre 2015
Autor de correspondencia: cmarin@usfq.edu.ec

Resumen: Partiendo de la ecuación que relaciona el parámetro de corrimiento hacia el rojo con el tiem- po y las densidades cosmológicas de materia, radiación y vacío en el modelo de Lemaitre, calculamos la edad del universo en el momento actual tomando en cuenta la contribución de la densidad de energía de la radiación (contribución que generalmente se desprecia en los cálculos). Adicionalmente calculamos el valor del parámetro de corrimiento hacia el rojo en la época de transición cuando materia y radiación se desacoplan.
Palabras clave: relatividad general, cosmología, Einstein, Friedmann, Lemaitre, corrimiento hacia el rojo.
Abstract: From the mathematical expression relating the redshift parameter with time and the cosmo- logical densities of matter, radiation and vacuum in the Lemaitre model, we have derived an equation for the age of the universe at present time taking into account the contribution of the radiation energy density (that generally is neglected in the calculations). Additiona- lly we calculate the value of the redshift parameter in the transition age when matter and radiation decouple.
Keywords: general relativity, cosmology, Einstein, Friedmann, Lemaitre, redshift.
Introducción
En el año 1922, el físico y matemático ruso Alexander Friendmann, usando las ecuaciones de campo de Einstein, probó que el universo debería estar expandiéndose a cambio de que dos suposiciones básicas fueran ciertas: “El universo es isótropo y homogéneo” [1, 2, 3]. La primera suposición (isotropía) nos dice que a gran escala (a nivel de galaxias, cúmulos y supercúmulos de galaxias en el espacio profundo) el universo parece el mismo en cualquier dirección que se observe. La segunda hipótesis (homogeneidad) dice que lo mismo sería cierto para un observador ubicado en otra galaxia. El descubrimiento de Hubble en 1929 de que el universo se estaba expandiendo, fue de allí, un gran triunfo para la Teoría General de la Relatividad (T.G.R.).
La evidencia de la isotropía del universo a gran escala se dio en 1965 cuando dos científicos americanos que trabajaban para los laboratorios de la Bell Telephone en Nueva Jersey, Arno Penzias y Robert Wilson, descubrieron un ruido de fondo (en forma de radiación de microondas) que parecía venir de los confines del universo. Esta radiación tiene un espectro térmico con una temperatura del orden de 2,726 grados Kelvin. El ruido de fondo cósmico es prácticamente igual en todas direcciones. La existencia del ruido o radiación de fondo cósmico de microondas (cosmic microwave background radiation), es entonces, una confirmación extremadamente precisa de la primera hipótesis de Friedmann sobre la isotropía del universo a gran escala. Por su descubrimiento, Penzias y Wilson, recibieron el premio Nobel de Física en el año 1978.
No hay evidencia científica a favor de la segunda hipó- tesis (la homogeneidad del universo a gran escala). En palabras de Stephen Hawking: “confiamos en ella sólo por razones de modestia” [3].
Vemos entonces que nuestro lugar en el universo no es especial. Un observador en una estrella de una galaxia distante vería un universo muy similar al que observamos. A esta aserción se la conoce como “principio cosmológico”. En otras palabras, en cualquier instante, el universo aparecería el mismo para todo observador, sin importar el lugar en que se encuentre.
En enero de 1998, el grupo que conforma el proyecto Supernova Cosmology Proyect, dirigido por Saul Perlmutter [4, 5, 6, 2], dió a conocer los resultados de su análisis de la variación del parámetro de corrimiento hacia el rojo con respecto a la magnitud efectiva (brillo) de 42 supernovas distantes del tipo Ia (las supernovas más brillantes) recientemente descubiertas. Para sorpresa de todos, estas supernovas lucían más tenues de lo que se esperaba, de acuerdo con el modelo standard del universo, en el que la expansión es desacelerada. Sus observaciones parecen indicar que el ritmo de expansión del universo se está incrementando, es decir el universo se está acelerando. Dichos resultados fueron confirmados por un grupo de investigación independiente dirigido por Brian Schmidt (High-Z Supernova) [7]. Estas medidas son compatibles con un universo plano, en el que la constante cosmológica es diferente de cero. También dan soporte a la teoría de que el universo atravesó un período de violenta inflación, cuando la constante cosmológica dominó sobre los efectos gravitatorios dando paso a una fase de de Sitter de brevísima duración.
La métrica del espacio-tiempo que mejor describe la evolución del universo y está de acuerdo con el principio cosmológico es la de Friedmann-Lemaitre-Robertson- Walker FLRW [2, 8, 9, 10, 11, 1, 12].En coordenadas esféricas r, θ, φ se escribe:
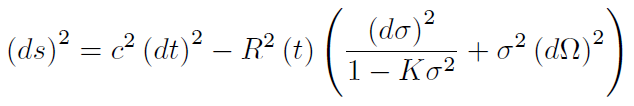 [1]
[1]donde c es la velocidad de la luz en el vacío, R (t) es el factor de escala del universo que depende del tiempo cósmico t y es proporcional al tamaño del universo, R. K es un parámetro independiente del tiempo que especifica la curvatura del universo y que puede ser K = 1 para un universo curvado en forma parecida a la superficie de una esfera (universo cerrado), K = -1 para un universo curvado en sentido contrario como la superficie de una silla de montar (universo abierto) y K = 0 para un universo plano. Finalmente (d)2 = (d_)2 + sin2_ (d_)2.
En este modelo el universo es como un fluido perfecto en el que las galaxias serían algo así como las partículas de dicho fluido siguiendo el movimiento del mismo [8]. El tiempo cósmico está dado por relojes en reposo con respecto al fluido cósmico, sincronizados con el instante en el que la densidad y la temperatura del fluido alcanzan un cierto valor esperado. Entonces, usando dichos relojes sincronizados, el estado físico del universo dependerá del tiempo en la misma manera en cualquier lugar.
El cuadrado del elemento de arco (ds). se puede escribir:
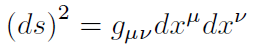 [2]
[2]donde el tensor métrico covariante está dado por la matriz:
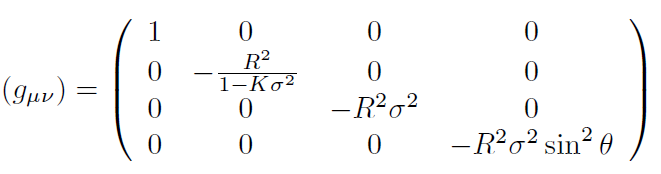 [3]
[3]El tensor contra variante correspondiente es:
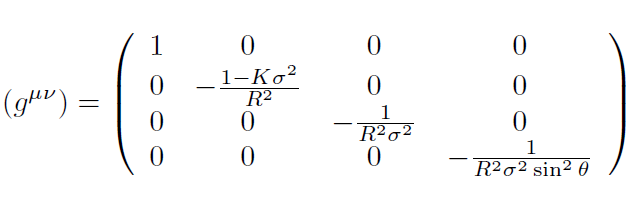 [4]
[4]Las ecuaciones de campo de Einstein son [7, 12, 17]:
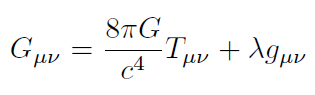 [5]
[5]con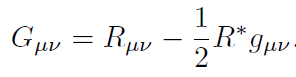
G es la constante de gravitación universal. En la anterior ecuación .. = gαβRαβ. A Rµν se le denomina tensor de Ricci, el cual se define a partir del Tensor de Riemann-Chirstoffel R. que determina la curvatura del espacio-tiempo. . donde
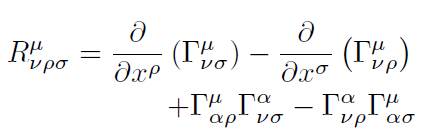 [6]
[6]. son los símbolos de Christoffel de segunda especie
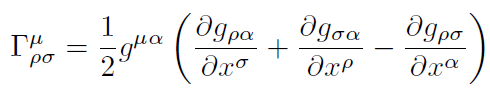 [7]
[7]. es la constante cosmológica introducida por Einstein en 1917 y es una medida de la contribución a la densi- dad de energía del universo debido a fluctuaciones del vacío.El valor de dicha constante es λ < 3 10−52 metros−2 [2, 13, 14].El término proporcional a . en las ecuaciones de campo de Einstein ( ecuación 5) pue- de ser interpretado como un tensor efectivo de energía- momentum dado por [15, 16] (ver particle properties databooklet)
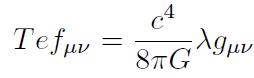 [8]
[8]Finalmente, Tµν es el tensor energía momentum que para un fluido perfecto (como el fluido cosmológico) es
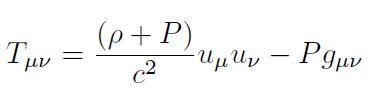 [9]
[9]donde . es la densidad de energía del universo y . es la presión del fluido cósmico. u. es el cuadrivector velocidad que en un marco de referencia comovil es u. = (c, 0, 0, 0).
Los elementos no nulos del tensor energía momentum son:
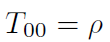 [10]
[10]
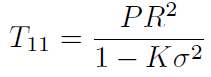 [11]
[11]
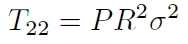 [12]
[12]
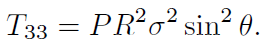 [13]
[13]Ya que la métrica es diagonal y el espacio es de máxima simetría [17] , Rµν = 0 si µ ν[17]:
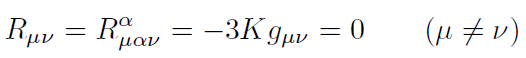 [14]
[14]Las componentes diagonales del tensor de Ricci son:
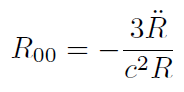 [15]
[15]
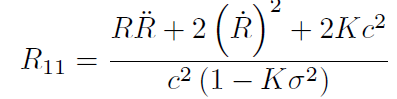 [16]
[16]
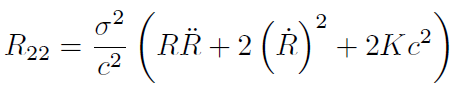 [17]
[17]
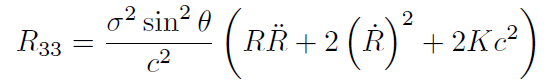 [18]
[18]A partir de estas expresiones, podemos calcular fácilmente el escalar de Ricci ..:
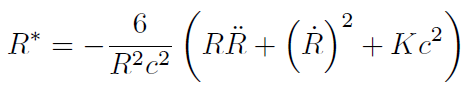 [19]
[19]y las componentes 00 y 11 del tensor de Einstein:
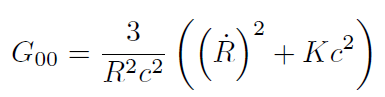 [20]
[20]
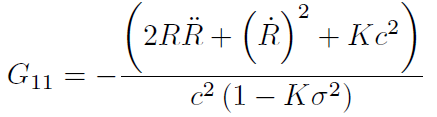 [21]
[21]Introduciendo las componentes 00 y 11 del tensor de Einstein y del tensor energía cantidad de movimiento en las ecuaciones de campo de Einstein obtenemos las ecuaciones de Friedmann
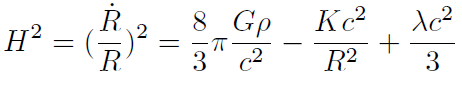 [22]
[22]
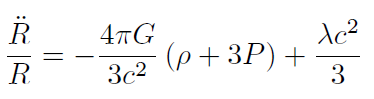 [23]
[23]donde . es el parámetro de Hubble que es una medida del ritmo de expansión del universo. Finalmente, ya que la derivada covariante del tensor energía-momentum es cero:
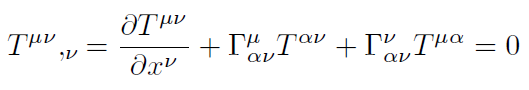 [24]
[24]tenemos, evaluando para . = 0, que
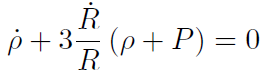 [25]
[25]Esta última relación también puede ser derivada a partir del primer principio de la termodinámica.
En la literatura [2, 14, 12, 18] se puede encontrar la expresión de la edad del universo en el modelo de Lemaitre (para un universo plano) calculada sin tomar en cuenta la contribución de la densidad de energía de la radiación. En el presente artículo calcularemos la edad del universo en un instante cualquiera y en particular en el momento actual teniendo en cuenta dicha contribu- ción. Adicionalmente deduciremos una expresión para el valor del parámetro de corrimiento hacia el rojo en la época de transición cuando materia y radiación se des- acoplaron aproximadamente 380000 años después de la Gran Explosión.
1 Ecuaciones de Friedmann y los parámetros cosmológicos
La ecuación de Friedmann (22) se puede escribir
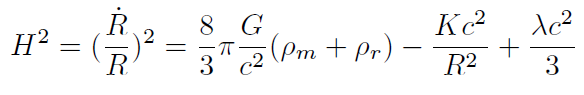 [26]
[26]donde ρ. y ρ. representan la densidad de energía de la materia y la radiación, respectivamente.
En términos de los parámetros cosmológicos de densidad de materia, radiación y del vacío
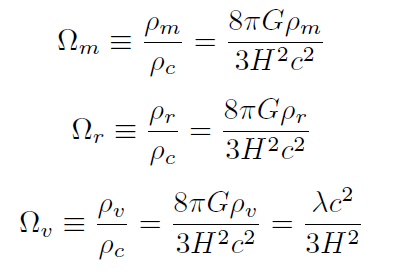 [27]
[27]donde ρ. es la densidad de energía del vacío [2, 18, 14], la ecuación (26) se puede escribir
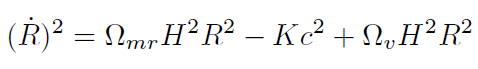 [28]
[28]donde Ωmr ..+Ω.. Recordando que (.˙ ). = ...., a partir de (28) obtenemos:
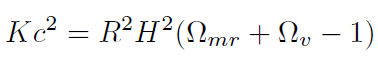 [29]
[29]La ecuación (29) nos da el parámetro de curvatura del universo en función de las contribuciones al parámetro de densidad cosmológica, el factor de escala y el parámetro de Hubble. Observaciones del proyecto WMAP9 y de Planck (2013) indican que el valor de la edad
del universo es de 13.800 0.038 Gyr, con un intervalo de confianza del 68 % y considerando el efecto BAO (Baryon Acoustic Oscillations)[19]. El modelo que es consistente con esta edad es el que propone . = 0, es decir, un universo plano. Reemplazando en (29), se ve claramente que:
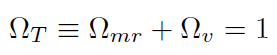 [30]
[30]Siendo Ω. la densidad cosmológica total. Es evidente que (30) es válida también en el momento actual. Igualmente (29) en el momento actual se se puede escribir Kc. = ....(Ω. . − 1).
Consideremos nuevamente la ecuación (25). Dicha ex- presión es válida para cualquiera de las densidades de energía (de materia, radiación o vacío). Asumamos una ecuación de estado de la forma . = ωρ donde . es una constante. Entonces, la ecuación (25) se puede escribir
Integrando esta ecuación obtenemos
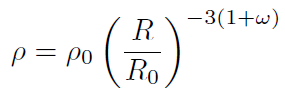 [31]
[31]donde .. y .. representan la densidad y el factor de escala del universo en el momento actual, respectiva- mente.
Entonces para cada uno de los tipos de densidades:
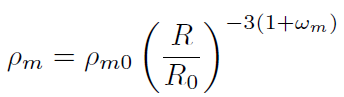 [32]
[32]
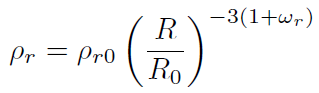 [33]
[33]
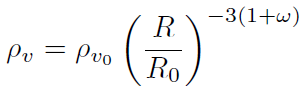 [34]
[34]donde ω. = 0, ω. = . y . = −1,00 ±0,06 [18]
Si . K= 0 y despreciamos la contribución de la densidad de energía de la radiación, la ecuación (28) se reduce a
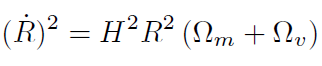 [35]
[35]que se puede también escribir:
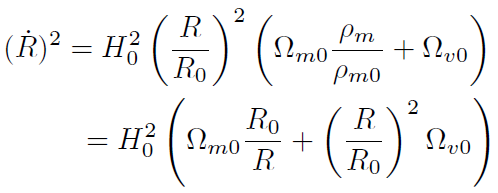 [36]
[36]
donde hemos usado la ecuación (32) con ω. = 0. La ecuación (36) se puede escribir utilizando separación de variables
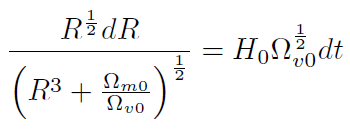 [37]
[37]Está expresión se puede integrar fácilmente haciendo el cambio de variable
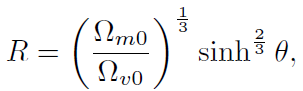 [38]
[38]el resultado es:
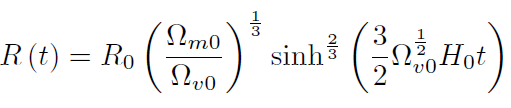 [39]
[39]A partir de (39) podemos calcular la edad del universo en el momento actual tmv. recordando que . (..) =... El resultado es la conocida expresión [2, 12, 14, 18]
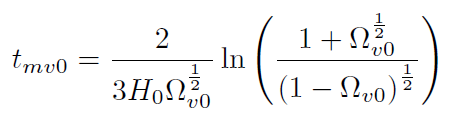 [40]
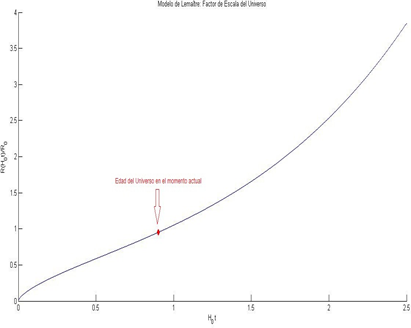
[40]donde hemos usado Ω.. + Ω.. = 1. En la figura (1) se representa el factor de escala del universo en función del tiempo.
2 Parámetro de corrimiento hacia el rojo y la edad del universo
El parámetro de corrimiento hacia el rojo se define a través de la ecuación
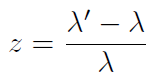 [41]
[41]donde λ es la longitud de onda de una línea espectral emitida por la fuente distante (dicha fuente es conocida en la Tierra), y λ/ es la longitud de onda observada en el espectro de la fuente de luz distante [2, 18, 20, 21]. Ahora, ya que: . ∝ .(.) y .. ∝ .(..) tenemos:
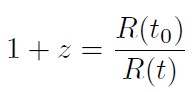 [42]
[42]Esto es equivalente a considerar que los eventos en galaxias cercanas se dilatan temporalmente acorde a cuánto el universo se ha expandido desde que el fotón que se observa fue emitido [21]. Esto es una consecuencia directa de la isotropía de la radiación de fondo cósmico.
Consideremos la expresión
que se puede escribir:
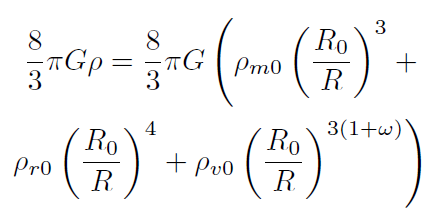 [43]
[43]donde .. = . (..). En términos de los parámetros cosmológicos de densidad tenemos:
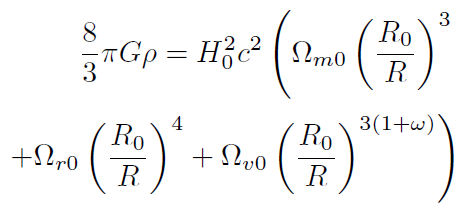 [44]
[44]Volviendo a la primera ecuación de Friedmann (22) y usando . = .πGρv tenemos que
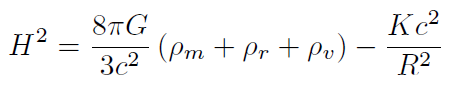 [45]
[45]Utilizando la ecuación (44) en la anterior ecuación tenemos que
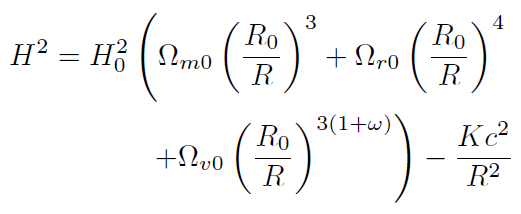 [46]
[46]Introduciendo el valor de Kc. dado en la expresión (29) (evaluado en el momento actual), (46) se escribe
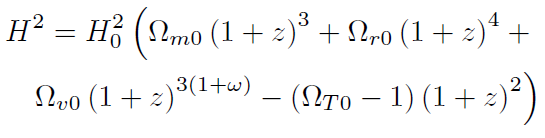 [47]
[47]donde Ω. . = Ω.. + Ω.. + Ω... En términos del parámetro de corrimiento hacia el rojo (ver (42)) la ecuación (47) se transforma en:
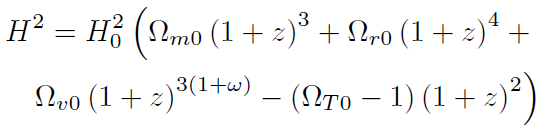 [48]
[48]Derivando (42) con respecto al tiempo se obtiene: .˙ =−., por lo que. Usando estos valores:
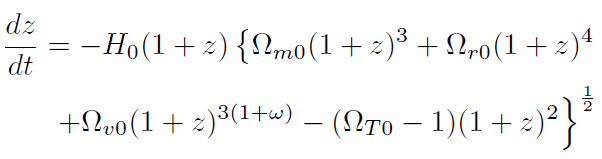 [49]
[49]A partir de esta relación haciendo separación de variables podemos calcular la edad del universo en un instante . cualquiera:
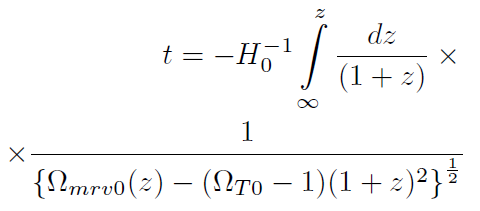 [50]
[50]Donde
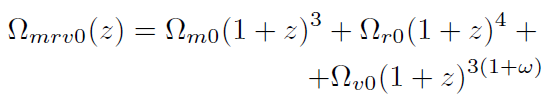 [51]
[51]Para un universo plano (K=0, Ω.0=1) tomando w=-1, la edad del universo en el momento actual se puede calcular a partir de la integral:
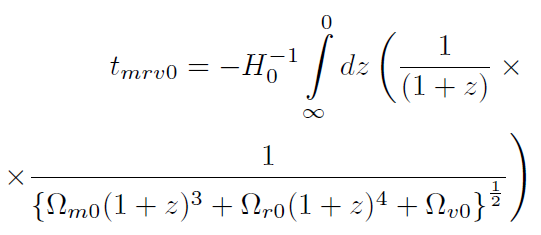 [52]
[52]Si no tomamos en cuenta la contribución de la densidad de energía de la radiación la integral se reduce a
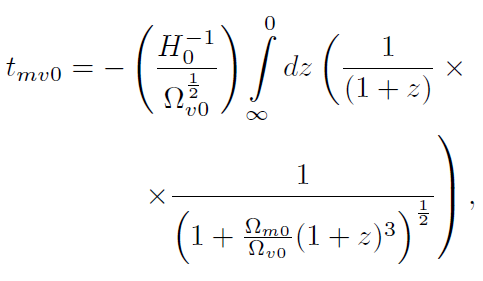 [53]
[53]y con el cambio de variable
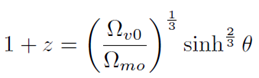 [54]
[54]la integral indefinida se transforma en
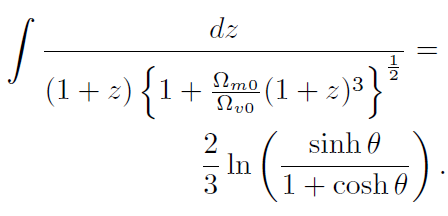 [55]
[55]Introduciendo la última integral en (53) junto con la expresión (54) y recordando que cosh . = 1 + sinh. . 2 tenemos:
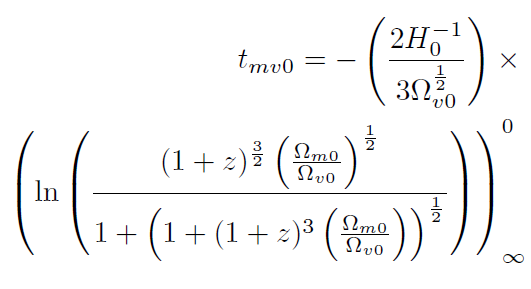 [56]
[56]Recordando nuevamente que Ω.. + Ω.. = 1, obtenemos nuevamente la expresión (40).
3 Edad del universo considerando la contribución de la densidad de energía de la radiación
Considerando un universo plano (ΩT 0 = 1) y tomando . = −1, la ecuación (50) se escribe:
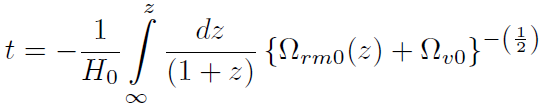 [57]
[57]donde
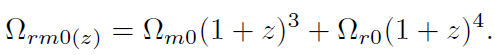 [58]
[58](57) también se puede escribir
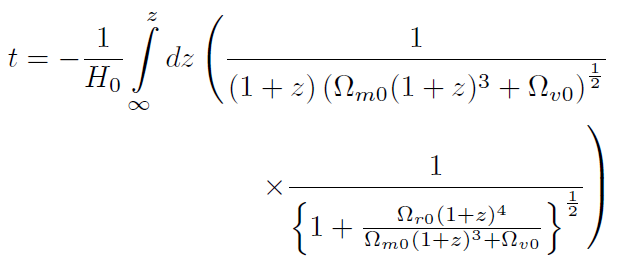 [59]
[59]Sin embargo, como Ω.. sigue siendo mucho menor que las otras dos densidades cosmológicas, se puede utilizar la aproximación a primer orden en serie de Taylor (1 +.). ≈ 1 + αε por lo que
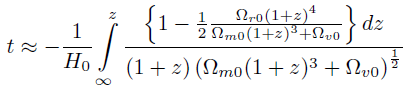 [60]
[60]Esta expresión puede ser separada en dos términos:
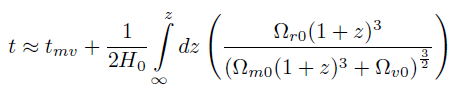 [61]
[61]donde
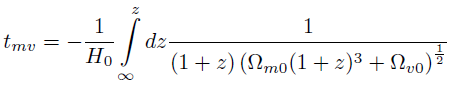 [62]
[62]Que también se puede escribir
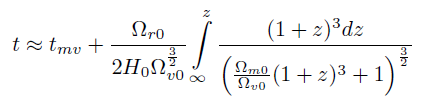 [63]
[63]Se ve claramente que cuando z entonces v. Si queremos calcular la edad del universo en el momento actual, entonces debemos hacer el parámetro de corrimiento hacia el rojo igual a cero. Se tiene entonces:
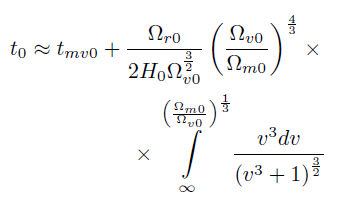 [64]
[64]donde tmv0 está dado por la ecuación (40). La última integral se puede dividir en dos integrales que se pueden resolver sólo de manera numérica:
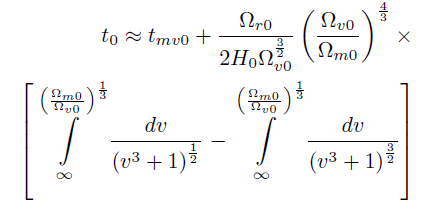 [65]
[65]Reemplazando el valor de tmv0 , se encuentra el valor analítico de la edad del universo en el momento actual considerando la contribución de todas las densidades cosmológicas:
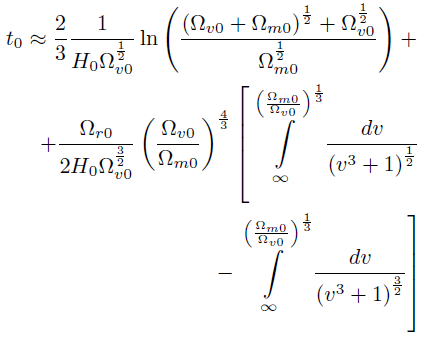 [66]
[66]Considerando que Ω.. + Ω.. 1 y tomando el valor principal de Ω.. = 0,685 [14, 19] el valor de las integrales es, calculado con la ayuda de Wolfram Alpha:
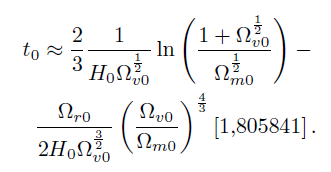 [67]
[67]En la tabla (1) se muestran valores numéricos de algunas edades del universo variando el parámetro H0, y consecuentemente también r0, con v0 = 0;685 y m0 = 0;315 [22]. Nótese que la corrección es relevante ya en el tercer decimal... ¡La corrección es del orden de los millones de años!
| Ωr0 | H0[Km/ (s Mpc)] | t0[Gyr] | Corr.[Gyr] | tmv0[Gyr] |
| 5.792× 10−5 | 65.3 | 14.24778 | 0.00389 | 14.25167 |
| 5.619× 10−5 | 66.3 | 14.03299 | 0.00372 | 14.03671 |
| 5.453× 10−5 | 67.3 | 13.82459 | 0.00355 | 13.82814 |
| 5.294× 10−5 | 68.3 | 13.62228 | 0.00340 | 13.62568 |
| 5.143× 10−5 | 69.3 | 13.42580 | 0.00325 | 13.42906 |
4 Cálculo del parámetro de corrimiento hacia el rojo en la época de transición
En un momento en la vida del universo temprano ocurrió una transición en donde el dominio de la densidad cosmológica de la materia siguió al dominio de la densidad correspondiente a la radiación. Durante la transición, sin embargo, existió un momento en el cual la densidad de energía de materia fue igual a la densidad de energía de la radiación, mientras que en comparación la densidad de energía del vacío era completamente despreciable. Al parámetro de corrimiento hacia el rojo evaluado en ese momento lo llamaremos zeq, y ocurrió aproximadamente 380000 años después de la Gran Explosión [23, 2]. Usaremos de nuevo la ecuación (50) con el límite superior de la integral igual a zeq, v0 = 0 ,T0 = 1 y definiendo el parámetro
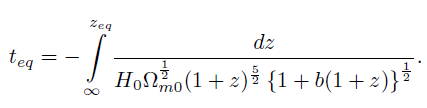 [68]
[68]Se usa el cambio de variable u = 1 + z, con lo cual ueq = 1 + zeq y por lo tanto
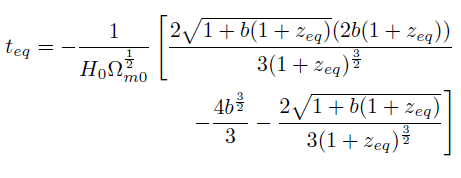 [69]
[69]Sin embargo, Lo que se quiere es encontrar zeqen función del tiempo de equilibrio. La última relación se puede escribir:
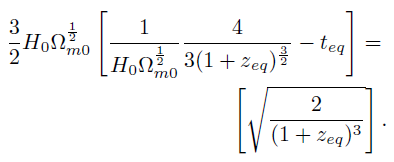 [70]
[70]Por otro lado, recordando que R = R0/1+z , tenemos que b = 1/1+z. En el momento en que las densidades de energía de materia y radiación son iguales podemos escribir beq = 1/1+zeq.
Reemplazando esto en la ecuación (70):
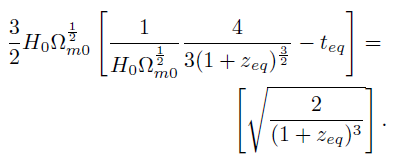 [71]
[71]De la última ecuación obtenemos:
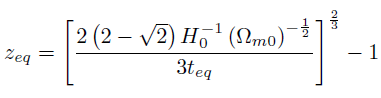 [72]
[72]En la tabla (2) se encuentran valores del parámetro de corrimiento hacia al rojo en el momento en que las den- sidades de energía de la materia y de la radiación eran iguales para diversos ...
| Ωm0 | teq[yr] | H0[Km/ (s Mpc)] | zeq |
| 0.315 | 380000 | 65.3 | 908.77534 |
| 0.315 | 380000 | 66.3 | 899.60412 |
| 0.315 | 380000 | 67.3 | 890.66059 |
| 0.315 | 380000 | 68.3 | 881.93584 |
| 0.315 | 380000 | 69.3 | 873.42142 |
5. Conclusiones
La Teoría General de la Relatividad (TGR) se resume en 14 ecuaciones: Las ecuaciones de campo de Einstein (10 ecuaciones) y las ecuaciones de las geodésicas (4 ecuaciones) [2, 8, 10]. Utilizando las ecuaciones de campo, se puede determinar la métrica del espacio-tiempo para una distribución dada de materia o energía. Por ejemplo, la geometría del espacio-tiempo de un universo isótropo y homogéneo en expansión está dada por la métrica de Friedmann-Lemaitre-Robertson-Walker. La mencionada métrica, al ser introducida en las ecuaciones de campo de Einstein, da origen a las ecuaciones de Friedmann. En el caso del modelo de Lemaitre para un universo plano (K = 0), a partir de dichas ecuaciones, se puede calcular como el factor de escala del universo va- ría en el transcurso del tiempo y deducir una expresión para la edad del universo sin tomar en cuenta la contribución de la densidad de energía de la radiación.
La densidad cosmológica debido a la radiación es cuatro órdenes de magnitud menor a las correspondientes a la materia y al vacío. No es sorprendente entonces que el término que considera la densidad de energía de radiación sea despreciado generalmente en comparación con las otras dos densidades de energía. Sin embargo, en aras de analizar el modelo de Lemaitre en forma más completa, hemos calculado la corrección a primer orden dada al considerar la contribución debido a la densidad cosmológica de la radiación.
La expresión analítica de la edad del universo en el momento actual la hemos calculado a partir de una ecuación que relaciona el tiempo con el parámetro de corrimiento hacia el rojo y las densidades cosmológicas (ver ecuación 50). En primer orden, el valor analítico de la edad del universo en el momento actual tomando en cuenta la contribución de todas las densidades de energía es: (ver ecuación 66)
El primer término de la suma representa la edad del uni- verso en el modelo donde se desprecia la contribución de la radiación y que se puede encontrar en la literatura (ver referencia [2, 18, 14, 12]), mientras el segundo término representa la corrección debido precisamente a dicha radiación. Nótese que el segundo término es di- rectamente proporcional a Ωr0, el cual es del orden de 10−5. Por lo tanto, la magnitud de la corrección es efec- tivamente pequeña en comparación con el término prin- cipal. En la tabla (1) se muestran algunos valores para la edad del universo en el momento actual para ciertos valores del parámetro de Hubble H0 y la densidad cosmológia de la radiación Ωr0.La correción está entre los 0,00325[Gyr] para el valor superior de H0, y los 0,00389[Gyr] para el valor inferior de H0. La contribución de la radiación disminuye en aproximadamente tres millones de años la edad del universo en el momen- to actual.
Adicionalmente calculamos el valor del parámetro de corrimiento hacia el rojo (zeq) en el momento en que la densidad de energía de la materia se hizo igual a la den- sidad de energía de la radiación, es decir cuando materia y radiación se desacoplaron y el universo se hizo transparente a la luz.Para ello se utilizó la ecuación (50) despreciando el valor de la densidad cosmológica del vacío. Ya que se tiene una buena estimación de la edad del universo cuando existió este equilibrio entre materia y radiación (teq 380000 años), el valor de zeq resultó ser (ver ecuación 72)
En la tabla (2) se ilustran los valores de zeq para diferentes valores del parámetro de Hubble H0. Vemos que aproximadamente, el parámetro de corrimiento hacia el rojo para dicha época era alrededor de 900.
Referencias
[1] Weinberg, S. 2008. “Cosmology” Oxford University Press.
[2] Marin, C. 2011. “La Expansión del Universo, Una Introducción a Cosmología, Relatividad General y Física de Partículas, Segunda Edición”, USFQ, Quito-Ecuador.
[3] Hawking, S. 1998. “A Brief History of Time” , Bantam Books.
[4] Perlmutter, S. et al. 1998. “Discovery of a supernova ex- plosion at half the age of the universe”, Nature 391, p. 51.
[5] Perlmutter, S. et al. 1999. “Measurements of . and . from 42 high-redshift Supernovae”, Astrophys. J. 517, p. 565-586.
[6] Perlmutter, S. 2003. “Supernovae, Dark Energy, and the Accelerating Universe”, Physics Today 56 (4), p. 53-59.
[7] Schmidt, B. et al. 1998. “High-Z-Supernova Search”, Astrophys. J. 507, p.46
[8] Kenyon, I. R. 1996. “General Relativity”. Oxford University Press, Oxford, UK.
[9] Ohanian, H. C. 1976. “Gravitation and Spacetime”. W. W. Norton Company, Inc.
[10] Misner, C. W.; Thorne, K.S. and Wheeler, J. A. 1973. “Gravitation”, W. H. Freeman & Company, NY, NY.
[11] Cheng, T. P. 2005. “Relativity, Gravitation and Cosmo- logy. A Basic Introduction”, Oxford University Press.
[12] Kolb, E. W., Turner, M. S. 1994. “The Early Universe”, Addison Wesley.
[13] Marín, C. 2001. “El Origen del Universo”, Producciones Digitales Abya-Yala.
[14] Olive, K. A. et al. (Particle Data Group) 2014. “Review of Particle Physics”, Chinese Physics C. 38, No.9.
[15] Gliner, E. B. 1966. Sov. Phys. JETP. 22.
[16] Zeldovich, Y. B. 1968. Sov. Phys. USP. 11.
[17] Weinberg, S. 1972. “Gravitation and Cosmology”, John Wiley Sons, Inc.
[18] Hobson, M. P., Efstathiou, G. P. and Lasenby, A. N. 2006. “General Relativity. An Introduction for Physicists”, Cambridge University Press, Cambridge, UK.
[19] Ade, P. A. R. et al. (Planck Collaboration). 2014. “Planck 2013 results. XVI. Cosmological Parameters”, arXiv:1303.5076(astro-ph.CO).
[20] Hoyng, P. 2006. “Relativistic Astrophysics and Cosmology, A primer”, Springer Verlag.
[21] Peacock, J. A. 1999. “Cosmological Physics”, Cambridge University Press.
[22] Lahav, O., Liddle, A. R. 2014. “The Cosmological Parameters”, Chinese Physics C. 38, No.9, p. 345-352.
[23] Guth, A. H. 1997. “The Inflationary Universe”, Addison Wesley.
Notas de autor
cmarin@usfq.edu.ec

