Simulation of ultimatum game with Artificial Intelligence and biases
Simulación del juego del ultimátum con inteligencia artificial y sesgos
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
Received: 15 May 2021
Accepted: 09 May 2023
Abstract: In this research we have developed different experimental designs of the ultimatum game with artificial intelligence players, including different biases: altruism, envy, and fair-mindedness. These players have supervised and unsupervised methods as well as a biased and unbiased way of thinking, depending on the case. We used reinforcement learning and bucket brigade to program the artificial intelligence players in python, and our method gave us revolutionary rational thought for how strategies are updated after every round. Using these simulations and behavior comparisons, we answered the following questions: Does artificial intelligence reach a perfect sub-game equilibriumin the ultimatum game experiment? How would Artificial Intelligence behave in the ultimatum game experiment if biased thinking were included in it? These analyses showed an important result: artificial intelligence by itself does not reach a perfect subgame equilibrium as expected,whereas the experimental designs with biased thinking players do quickly converge to an equilibrium. Finally, we demonstrated that the players with envy bias behave the same as the ones with altruistic bias.
Keywords: Reinforcement Learning, Bucket Brigade, Homo-economicus, Biased thinking, Nash Equilibrium, Perfect sub-game equilibrium, Pareto Optimum, Artificial Intelligence and Ultimatum game.
Resumen: En esta investigación se han desarrollado diseños experimentales del juego del ultimátum con agentes inteligentes artificiales con el rol de jugadores, incluyendo distintos sesgos: altruismo, envidia y pensamiento justo. Se ha utilizado aprendizaje por refuerzo y bucket brigade para programar los jugadores en python, nuestro me´todo nos otorga un pensamiento racional evolutivo por como los jugadores actualizan sus posibles estrategias basado en los resultados de las rondas previas. Mediante simulaciones y comparación de comportamientos se han estudiado las siguientes preguntas: ¿Llega la inteligencia artificial a un equilibrio de subjuego perfecto en el experimento del juego del ultimátum? ¿Cómo se comportaría la inteligencia artificial en el experimento del juego del ultimátum si se le incluye un pensamiento sesgado?
Este análisis exploratorio ha llegado a un importante resultado: la inteligencia artificial por sí sola no llega a un equilibrio de subjuegos perfecto. Por otro lado, se demostró que los diseños experimentales de los jugadores con sesgo convergen a un equilibrio rápidamente. Por último, se demostró que los jugadores con sesgo de envidia se comportan igual que los que tienen sesgo de altruismo.
Palabras clave: Aprendizaje por refuerzo, Bucket Brigade, Homo-economicus, Pensamiento sesgado, Equilibrio de Nash, Equilibrio de subjuego perfecto, O´ptimo de pareto.
INTRODUCTION
The economists Guth, Schmittberger, and Schwarze were the first who introduced the ultimatum game to experimentation to test human responses. They concluded that humans do not take the strategies that lead to a Nash equilibrium because they are not rational. These findings motivated us to research what would happen in an experiment with rational players. Does artificial intelligence (AI) reach the perfect sub- game equilibrium in the continuous ultimatum game experiment? How would artificial intelligence behave in the ultimatum game experiment if we included biases?
To answer these research questions, we created a continuous ultimatum game experiment with different types of artificial intelligence players. We used two learning methods to program the players and created a distinction between biased and unbiased players. These different methodologies allowed us to study different behaviors and complement this research.
The contribution of this research to the empirical literature encompasses the areas of game theory, experimental economics, behavioral economics, and artificial intelligence. We expect to contribute to the growth of the AI research in the field of economics. The results we obtained can be used to compare human behavior with rational behavior and, furthermore, analyze the equilibrium variants that the experiments of the ultimatum game may have.
The research Learning to Reach Agreement in a Continuous Ultimatum Game published in 2008 by Steven de Jong and Simon Uyttendaele concluded that continuous-action learning is satisfactory when we are aiming to allow players to learn from a relatively low number of examples. Another research study published by Sanfey in 2003, under the title The Neural Basis of Economic Decision-Making in the Ultimatum Game, defined biases that influenced the agents’ decision-making in the ultimatum game experiments [17]. He explained that human beings’ behavior is far away from the assumption of homo- economicus. Some research studies have created an experiment of the ultimatum game using artificial intelligence players, but ours is the first to include the biases of altruism, envy and fair-mindedness, described by Sanfey, in artificial intelligence players.
On the other hand, Gale, Binmore, and Samuelson published research in 1995 under the name Learning To Be Imperfect: The ultimatum game that specified that the ultimatum game experiments do not reach the theoretical Nash equilibrium because of misconception [8], which also agrees with the research by Guy in 2011, entitled Decision making with imperfect decision makers, where the author used artificial intelligence to prove that the rational solution for Player 2 is to have more equitable payoff and to not converge to the Nash equilibrium [11]. Our contribution lies in creating different learning methods in artificial intelligence players to be able to verify or refute these theories.
In section 2 of our research, we expose the methodology that was used to construct the artificial intelligence players of the experimental design. We explain how rational players and biased players were defined. Section 3 details the obtained results for each type of player under different simulations. Section 4 offers conclusions and mentions possible research topics that could emerge from this research.
METHODOLOGY
The original ultimatum game
This game is a probabilistic situation in which there are two players; Player 1 (J1) splits an amount of 1 to Player 2 (J2). J1 proceeds to make an offer of how to split this amount defined as X ∈[0, 1]. J2 has to decide to accept or reject the offer. If it is rejected, J1 and J2 will get a payoff equal to 0. If it is accepted, J2 will obtain the value offered by J1.
The original game works in one round, and therefore, there is only one chance to take the right decision. This “right decision” equals a rationality assumption called the Nash equilibrium. The model of this game is better described in Figure 1.
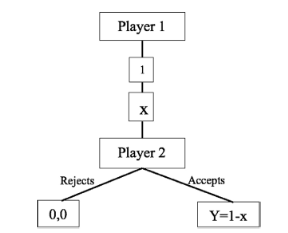
Figure 1.
Original Ultimatum Game
Figure 1 tree diagram shows Player 1 and Player 2. The amount to be split is 1 unit and the strategy of Player 1 is represented as x, where x takes an interval value of real numbers between 0 and 1. Furthermore, for each value of x, Player 2 will have a payoff of 0 in case of rejecting or 1 − x in case of accepting. To simplify the nomenclature, (1 − x = y) is defined as the player payoff.
Economic science establishes that each player, if behaving rationally, must converge to the Nash equilibrium (0,9,0,1). Thus, the academic text A primer in game theory, written by Gibbons in 1992, explains that Player 1 always will approach the maximum possible amount for itself and will offer the smallest possible amount to Player 2. Player 2 will accept any value greater than 0, since in any other case it is indifferent between accepting or rejecting the offer [9]. Therefore, to reach the theoretical equilibrium inrepeated games, there must be an adjustment such that the player strategies reach Nash equilibrium in 1 round or sub-game cycle. This happens because there is no rational strategy that deviates these payoffs from Nash equilibrium.
The continuous ultimatum game
In the continuous ultimatum game, Player 1 splits the same amount (0,9,0,1) in N iterations. Since in each round the rational decision remains the same, there is no reason to deviate from the Nash equilibrium value even if there are more rounds. The most optimal decision always remains for Player 1 to select the maximum possible value and for Player 2 to accept any value greater than 0. This statement can be seen by the backward induction process in Figure 2.
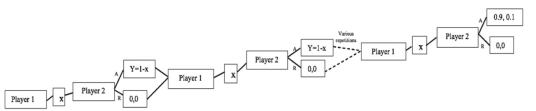
Figure 2.
Backward induction of the Ultimatum Game
Figure 2 shows that in each round the same rational decision is made. Therefore, the backward induction process shows that the Nash equilibrium is the same in the sub- games. There are no possible triggering strategies.
Experimental design of the ultimatum continuous game
Our experimental design of the ultimatum game is composed of 1000 rounds to ensure that players reach a convergence. We implement 2000 players, 1000 couples of players to generate a large database that allows us to identify a pattern. The value to be split between the two players is 10 units, which will be the same every round until the end of the experiment. The distribution of 10 units will be in integer numbers to facilitate the extraction of our database.
At the beginning of the experiment, each player is assigned a role, Player 1 (bidder) or Player 2 (receiver), and they are matched. The role remains the same until the end of the experiment, and each player remains with the same partner within the whole experiment. All Player 1 strategies are defined by S1 and all Player 2 strategies are S2. In the first round, Player 1 and Player 2 randomly draw an integer from the interval [1,..., 10], which is contained in vector V1 and V2, respectively, to define the strategies, respectively. Player 2 will accept or reject Player 1’s strategy by comparing S1 and S2 so the players can update their future strategies. The diagram detailing our experimental design is shown in Figure 3. In case Player 2 rejects, both will receive a payoff (0,0). In case Player2 accepts, Player 2 will get the split proposed by Player 1 (S1,10-S1).
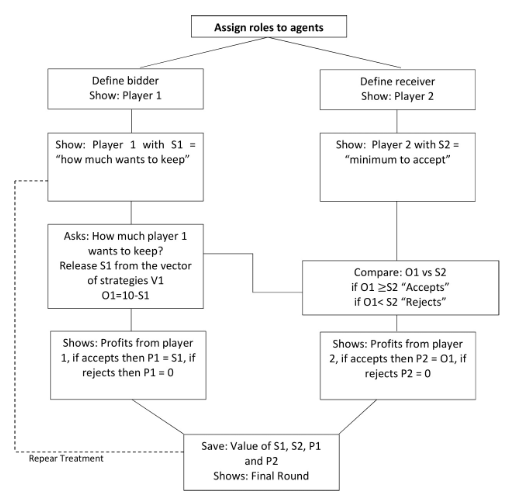
Figure 3.
Ultimatum Game Experimental Design
At the end of this experiment, the strategies of the players should converge to (9,1) according to the economic theory. However, research published by Román Carrillo in 2009, Cooperación en redes sociales: el juego del ultimátum, showed this same experimental design with human beings and came to the conclusion that few individuals end up with offered amounts above fifty percent [16]. The ultimatum game played with human players make an output similar to the Nash equilibrium impossible. Human beings do not act rational on the maximization of benefits and endowments. This gives us the premise of the importance of evolutionary rational thought and quantifying bias.
Pseudo-code of the ultimatum continuous game experiment
The experimental environment is programmed by defining two players for each round, Player 1 and Player 2, from a list of 2000 players. Each player is matched. S1 is defined by V1 and S2 is defined by V2. Then, O1= 10-S1 is defined. Strategies function: each player chooses a strategy from the vector V1 or V2. Comparison function: Player 2 compares O1 vs S1 and makes a decision: if O1>=S2, Player 2 accepts; if O1<=S2, Player 2 rejects.
Payoff function (payoff Player 1 = P1 and payoff Player 2 = P2): If Player 2 accepts, P1 = S1 and P2 = O2; if Player 2 rejects, P1 = 0 and P2 = 0. Saves value of S1, S2, P1, and P2. The game is repeated 1000 times after the strategies are chosen.
Behavioral economics
Our players update the strategies in five different games for which three of them are set by three types of biases: altruism, envy, and fair-mindedness. We considered it important to include these biases in our experimental design to enrich our research. Sanfey’s research Social Decision-Making: Insights from Game Theory and Neuroscience Science in 2007 demonstrated that some biases most prevalent in the ultimatum game experiment are altruism, envy and fair-mindedness [18].
To include these biases in our experimental design, it was necessary to create a function called welfare function that allows our Players 1 and Players 2 to evaluate the payoff based on the bias assigned. The payoffs versus the payoffs of the partners (see figure 6, 7 and 8). In this way, we were able to create a new metric called ”welfare,” which allowedus to further the analysis of our research.
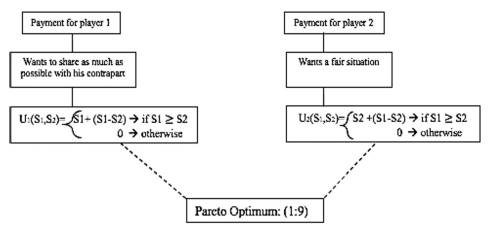
Figure 6.
Altruistic Player Diagram
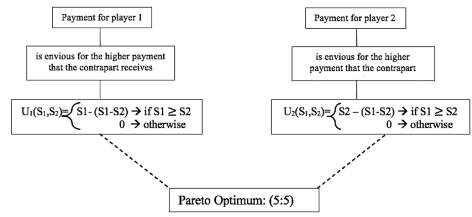
Figure 7.
Envious Player Diagram
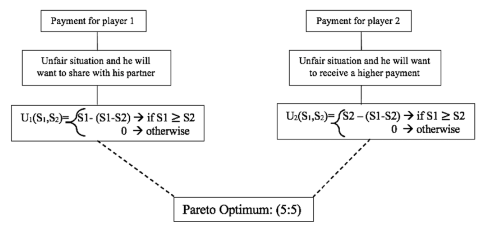
Figure 8.
Fair-Minded Player Diagram
The purpose is to measure what occurs to each player’s strategies, payoffs, and welfare when they behave exclusively altruistically, enviously, or fairly. These results were compared with unsupervised players without bias (rational players fulfill all economic assumptions for a perfect equilibrium in sub-games) and supervised players without bias (rational players always converge to perfect equilibrium in sub-games).
The players’ behavior in our experiment are defined as follows: . is the payoff of Player 1 and . is the payoff of Player 2:
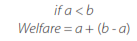
Altruistic
In this bias, the players maximize the welfare when the partner has a payoff value greater than itself. Its welfare is the payoff it receives plus the surplus from the partner.
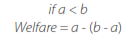
Envious
When the player has a lower payoff than its partner, its welfare decreases. Its welfare is the payoff that each player receives minus the other player surplus.
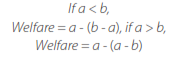
Fair-minded
Each player finds it unfair to have unequal payoff. If Player 1’s payoff is higher than Player 2’s payoff, Player 1’s welfare goes down, but if the payoff is higher than Player 2’s payoff,the same thing happens. Each player maximizes the welfare with a fair split.
Figures 6, 7 and 8 detail how biases work in the experiment defined above. It is important to mention that, when there is a biased behavior, the expected equilibrium responses reach a point known as the pareto optimum.
Artificial intelligence in our experimental design
Artificial intelligence is defined as a set of algorithms that seek to mechanically recreate certain behaviors. Our research is not the first to use evolutionary algorithms in an ultimatum game experiment; indeed, the research Learning to Reach Agreement in a Continuous Ultimatum Game by de Jong et al. implemented players with continuous action learning automata in a large number of random pairwise games in order to establish a common strategy [5]. However, it is the first to incorporate the aforementioned biases in the artificial intelligence players.
In our experimental design, we use the reinforcement learning mechanism bucket brigade. This mechanism is defined by a chain of buckets, where in every round the buckets fill with more information that will converge to the best strategy. The first-round players randomly choose an integer number between 1 and 10 from a vector V1 and V2 that contains all these possible strategies. After playing the first round, the vector of strategies updates by how effective the strategies were. For example, if Player 1 proposes to keep 9 of the 10 units to be split and Player 2 accepts that proposal, the player will add 9 times the strategy 9 at the vector V1 and Player 2 will add 1 time the strategy 1 at thevector V2. This method favors the strategies that pay best, guaranteeing a reinforcementlearning and allowing us to have the player with rational evolutionary learning, abehavior similar to how human beings play in real life.
We created two different types of algorithms to extend our analysis. The first algorithm follows the supervised learning method which has an adjustment, a fixed target point for the players to update the strategy vectors to reach the Nash equilibrium. The second, known as unsupervised learning, is for players to update the strategy vectors using the bucket brigade mechanism and to learn from the previous strategies until reaching a convergence that they consider the best strategy to play.
We created players with the supervised learning method and with the unsupervised method, shown in figures 4 and 5. Also, we created players with the unsupervised learning method and with three different types of biases: altruism, envy, and fair- mindedness. Consequently, these players do not work with an adjustment, and therefore, players are expected to take trigger strategies.
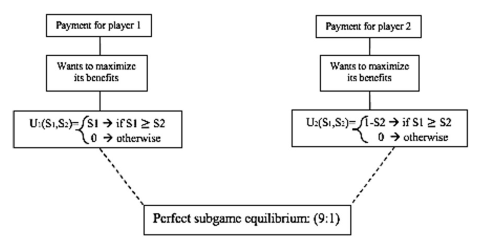
Figure 4.
Non-biased Supervised player Diagram
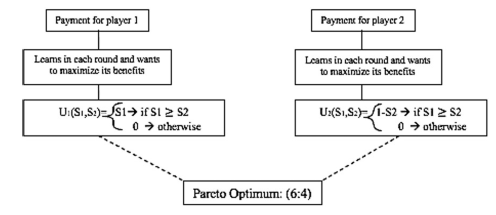
Figure 5.
Non-Biased Unsupervised Player Diagram
Pseudo-code for the creation of class players
Define each player as an object with a role, bidder = Player 1 and receiver = Player 2. Initial parameters for each player: role, S1 defined by V1, S2 defined by V2, V1 [1,10], V2 [1,10], payoffs, accumulated payoffs, welfare, and accumulated welfare. Create a function to choose the strategy: make a random choice from V1 and V2. Comparison function: Player 2 compares O1 vs S2. If O1 >= S2, Player 2 accepts. If O1 <= S2, Player 2 rejects. Each player’s profits are displayed. Player 1: if Player 2 accepts, then P1 = S1; if Player 2 rejects, then P1 = 0. Player 2: if accepts, then P2 = O1; if rejects, P2 = 0. Saves value of S1, S2, P1 and P2. Shows: final round. The treatment is repeated, and each player accumulates the payoff or welfare at the end of each round. a is Player 1’s payoff and b is Player 2’s payoff, detailed below.
Pseudo-code of the supervised learning without bias
Define each player with the previous parameters. Strategy update function: as long as Player 1’s payoff >= 9, Player 1 adds n times the strategy n at the vector V1. As long as Player 2’s payoff <= 1, Player 2 adds n times the strategy n at the vector V2. The players update the strategies without a bias.
Pseudo-code of the unsupervised learning without bias
Define each player with the previous parameters. If Player 2 accepts, O1>=S2, and each player adds n times the strategy n at the vector V1 or vector V2, respectively. The players update the strategies without a bias.
Pseudo-code of the unsupervised learning with altruism
Henceforth . is Player 1’s payoff and . is Player 2’s payoff, detailed below.
Define each player with the previous parameters. Altruistic bias function: if a < b, the player obtains a welfare = a + .b - a); otherwise, player welfare = a. Strategy update function: the player updates the strategy n times the strategy n that gives a welfare > 0. Welfare accumulation function: the player saves the welfare and accumulates it.
Pseudo-code of the unsupervised learning with envy
Define each player with the previous parameters. Envy bias function: if a < b, the player obtains a welfare = a - (b - a); if not, player welfare = a. Strategies update function: the player updates the strategy n times the strategy n that gives a welfare > 0. Welfare accumulation function: the player saves the welfare and accumulates it.
Pseudo-code of the unsupervised learning with fair-mindedness
Define each player with the previous parameters. Fair-minded bias function: if a < b, the player obtains a welfare = a - (b - a); or, if a > b, obtains a welfare = a - (a - b). If not, the welfare = a. Strategies update function: the player updates the strategy n times the strategy n that gives a welfare> 0. Welfare accumulation function: the player saves the welfare and accumulates it.
Data collection
Our data collection is a method that combines experimental design with artificial intelligence programming. Data were generated after running the simulations and saving the generated data.
RESULTS
Ultimatum game with players without bias (supervised learning)
Figures 9 and 19: The strategies and payoffs made by Player 1 and Player 2 converged to a perfect sub-game equilibrium of (9,1). Player 2 tended to accept any offer greater than zero, while Player 1 repeatedly continued to offer as little as possible, as the theory stipulated. However, there were rounds in which Player 2 declined the offer, waiting for a change in Player 1’s strategy. In this case, the players ended up ratifying the perfect sub-game equilibrium.
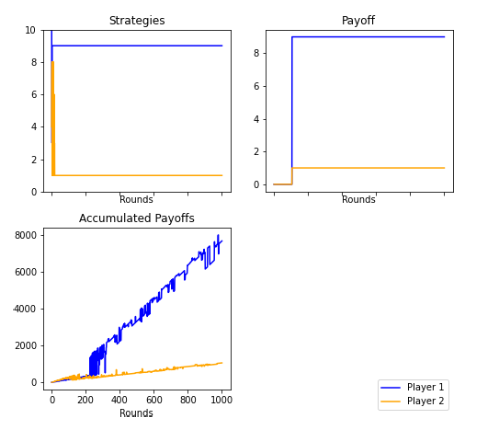
Figure 9.
Supervised Player. 1000 rounds. Mode
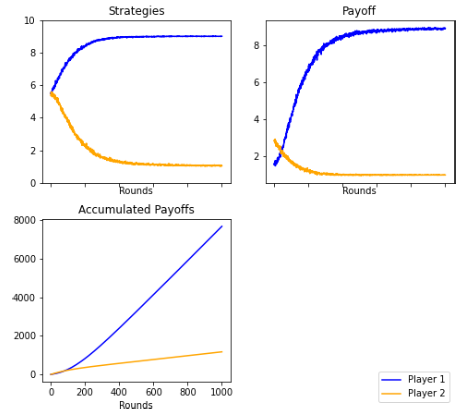
Figure 19.
Supervised Player. 1000 rounds. Average
Figure 14: The evolution of the strategies is shown in a histogram where in the first round the players randomly choose a strategy, and after 500 rounds, Player 1 and Player 2 play for strategies 9, but in round 1000 each player converges to the Nash equilibrium.
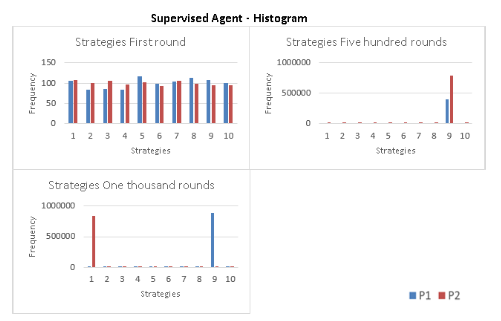
Figure 14.
Supervised Player. Histogram
Ultimatum game with players without bias (unsupervised learning)
Because the players have bucket brigade learning and memory, they have a different maximization environment. Player 1 and Player 2 strategies evolve and converge for the strategies that give them the best payoffs.
There was a more concurrent rejection of the minimum offers. This simulation has been repeated multiple times and has been found to be statistically valid. Artificial intelligence by itself (without supervision) reaches a different equilibrium than the Nash, a pareto optimum, against our expectations.
Figures 10 and 20: Unlike the previous experimental design, the results changed significantly.
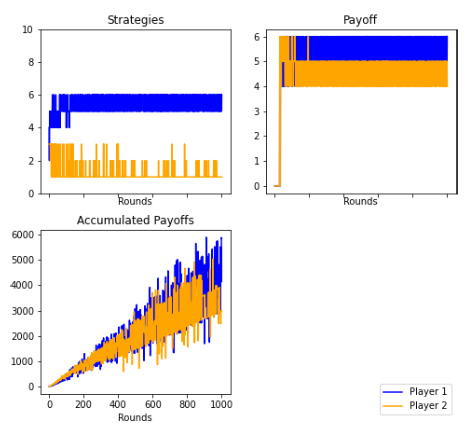
Figure 10.
Unsupervised unbiased Player. 1000 rounds. Mode
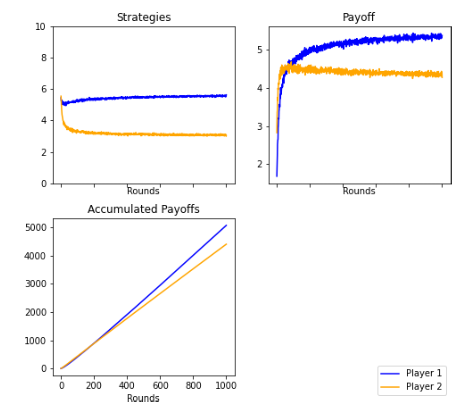
Figure 20.
Unbiased Player. 1000 rounds. Average
The players do not converge to a perfect sub-game Nash equilibrium, but to a pareto optimum. In this situation, artificial intelligence behaves similarly to a human being. A balance is reached between (6,4) and (5,5).
Figure 15: The evolution of the strategies is shown in a histogram where in the first round the players randomly choose a strategy, and after 500 rounds Player 1 and Player 2 play for strategies close to 5, but in round 1000 Player 1 converges more for a strategy close to 5 and Player 2 for strategies lower than 5.
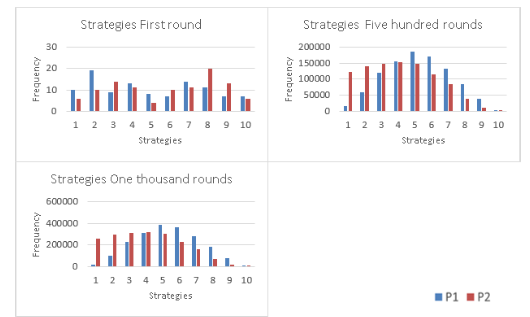
Figure 15.
Unbiased Player. Histogram
Trigger strategies emerged. Player 1 made increasing offers. The roles changed and now it was Player 2 who had the greatest power in deciding the appropriate offer to maximize the benefits.
Ultimatum game with altruism bias (unsupervised learning)
Unlike the first two experimental designs, this one is characterized by the fact that the players have a bias that conditions them. According to the designed algorithm, the players tended to keep as little as possible so that the partner received the greatest benefit.
Figures 11 and 21: In this case, the results converge to a pareto optimum of (1,9). Player 2 continually rejected offers by Player 1 that were considered high, so Player 2 eventuallyended up delivering lower offers. Being altruistic generates a result totally opposite tothe Nash equilibrium.
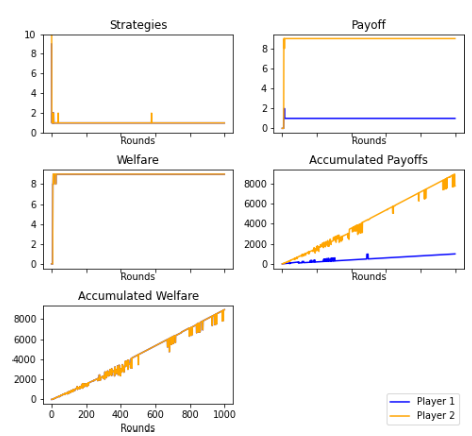
Figure 11.
Altruistic Player. 1000 rounds. Mode
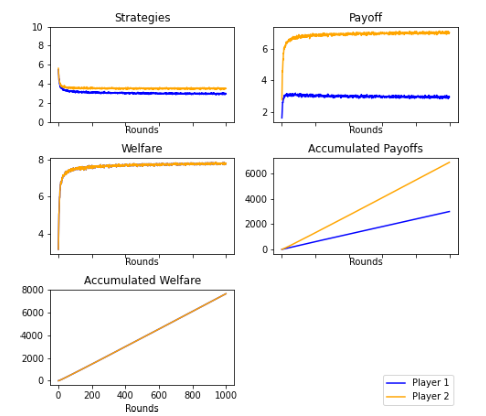
Figure 21.
Altruistic Player. 1000 rounds. Average
Figure 16: The evolution of the strategies is shown in a histogram where in the first round players play randomly, and after 500 rounds Player 1 and 2 play for strategies close to 1. In round 1000 each player converges more for strategies close to 1, keeping the tendency.
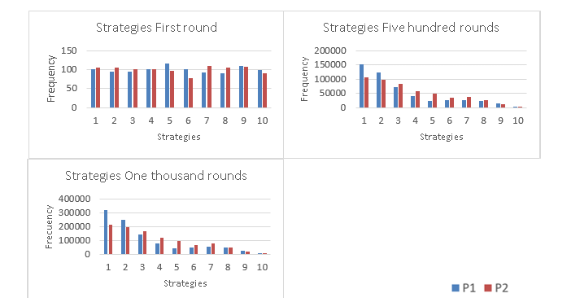
Figure 16.
Altruistic Player. Histogram
Ultimatum game with envious bias (unsupervised learning)
The possibility of higher rewards was found biased due to the perception of an envious environment. It was more likely to have a reject strategy between rounds. The figure below shows the results for this case.
Figures 12 and 22: It is denoted that the players converged to a pareto optimum of (5,5). Player 2 continually declined minimum offers until Player 1 changed his strategy. Player 1 and Player 2 eventually settled for that combination that does not generate envy. Theplayers reached a point where neither was envious of the other.
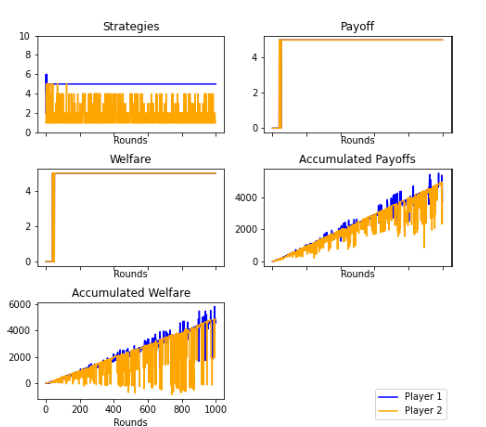
Figure 12.
Envious Player. 1000 rounds. Mode
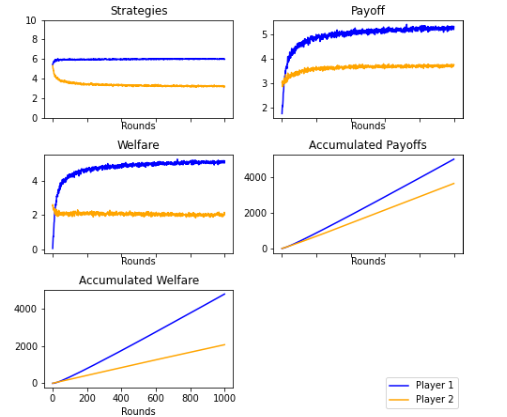
Figure 22.
Envious Player. 1000 rounds. Average
Figure 17: The evolution of the strategies is shown in a histogram where in the first roundplayers play randomly, and after 500 rounds Player 1 plays for strategies close to 5 and2 for any strategies lower than 5. In round 1000 Player 1 plays strategy 5 with morefrequency than others, and Player 2 plays more strategies that are lower than 5.
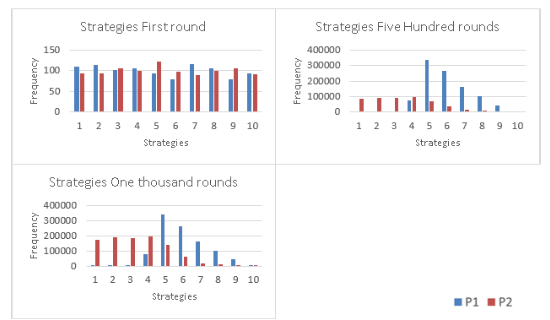
Figure 17.
Envious Player. Histogram
Ultimatum game with fair-minded bias (unsupervised learning)
Figures 13 and 23: Fair-minded bias allowed players to maximize the welfare by having fair payoffs between rounds. The figure shows these results. They reached a pareto optimum of (5,5). Player 1 and 2, despite not maximizing their payoffs, maximized their welfare when the benefits were equal. Player 2 continually rejected minimum and maximum offers, and Player 1 delivered offers with increasingly fair pay.
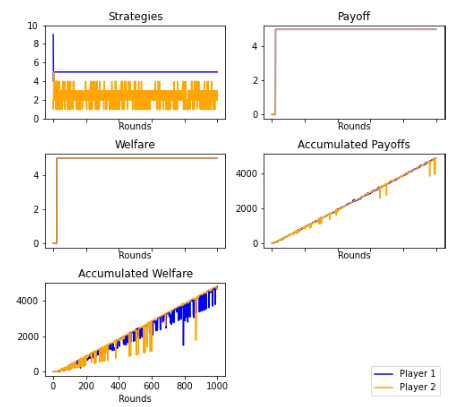
Figure 13.
Fair-Minded Player. 1000 rounds. Mode
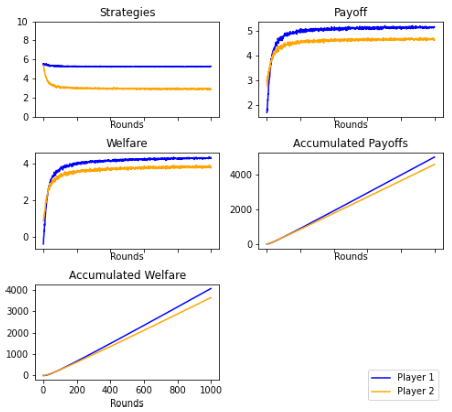
Figure 23.
Fair-minded Player. 1000 rounds. Average
Figure 18: The evolution of the strategies is shown in a histogram where in the first round players play randomly, and after 500 rounds Player 1 converges for strategies close to 5, and Player 2 plays for strategies lower than 5. In round 1000 Player 1 converges more for the strategy 5, and Player 2 for strategies lower than 5.
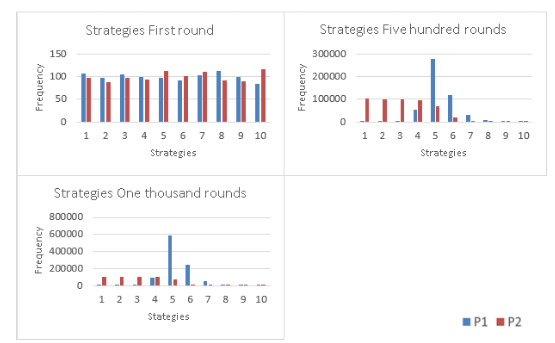
Figure 18.
Fair-minded Player. Histogram
CONCLUSIONS AND RECOMMENDATIONS
The most important conclusion of this research is that, contrary to expectations, unbiased artificial intelligence with unsupervised learning does not lead players to the Nash equilibrium. The research Learning To Be Imperfect by Gale, Binmore, and Samuelson explains that this happens because artificial intelligence players learn between rounds [8]. In our experiment, Player 2 discovers that in order to maximize the future profit, it has to give up the current gains. This research shows that artificial intelligence alone (without supervision) includes trigger strategies that lead to a convergence of a pareto optimum, not a Nash sub-game equilibrium.
Also, in the research Learning to Reach Agreement in a Continuous Ultimatum Game, rational evolutionary learning is the main explanation of how humans play and make decisions in real life. Humans like artificial intelligence based on reinforcement learning, in our research bucket brigade, upgrade the strategies based on the results of the previous rounds [5]. This is why our unbiased unsupervised players play similarly to how humans play a continuous ultimatum game, and it implies the importance and relevance of studying how artificial intelligence based on reinforcement learning can be used to predict how human beings act in particular events.
On the other hand, our results show that biased artificial intelligence quickly converges to an equilibrium point. One particular case gave us an important result, where the envy bias ended up bringing players to the same equilibrium as fair-minded bias. This happens because the payoff (5,5) is the only point at which players are not envious, so they behave fairly.
Finally, artificial intelligence with supervised learning converges in a matter of a few rounds to the Nash equilibrium (9,1), almost instantaneously. This can be explained by the fact that this method is programmed with an adjustment that pushes the players to equilibrium of perfect sub-games. As players know where to go, they update the strategies to reach this point. We include the publication of Gale, Binmore, and Samuelson when mentioning that the learning method of the players influences the possible strategies [8].
This research could be extended by using combinations between different types of players to identify new behaviors. Also, degrees of bias could be added to measure what would happen if the player behaved, for example, doubly envious. The experimental design could be altered with a change of roles for the players as they play. It is even possible to establish different models of equilibrium, macroeconomics, microeconomics, and others with the help of players with artificial intelligence.
ACKNOWLEDGEMENTS
We thank ACI Avances en Ciencias e Ingenierías for the opportunity to publish this research. We are hopeful to contribute to further research that can innovate science and the way of thinking. We also thank Universidad San Francisco de Quito USFQ for allowing the development of this research.
AUTHOR CONTRIBUTIONS
Julio Añasco: research administration, methodology design, software development, writing and draft review; Bryan Naranjo and Pamela Proaño: elaboration of figures, validation and verification of results, software development, writing and draft review; Anastasia Vasileuski: software development, writing original draft and literature review. Edited by Julio Añasco y Pamela Proaño.
REFERENCES
[1] Sanfey, A., Rilling, J., Aronson, J., Nystrom, L., & Cohen, J. (2003). The Neural Basis of Economic Decision-Making in the Ultimatum Game, (2003). Science, 300(5626), 1755-1758. doi: https://doi.org/10.1126/science.1082976
[2] Gale, J., Binmore, K. & Samuelson, L. (1995). Learning to be imperfect: The ultimatum game. Games and economic behavior, 8(1), 56-90. doi: https://doi.org/10.1016/S0899-8256(05)80017-X
[3] Guy,T.V., Kárny´, M., & Wolpert, D. H. (Eds.). (2011). Decision making with imperfect decision makers (Vol. 28). Springer Science Business Media. doi: https://doi.org/10.1007/978-3-642-24647-0
[4] Gibbons, R. (1992). A primer in game theory. Pearson Academic.
[5] Román Carrillo, J. (2009). Cooperación en redes sociales: el juego del ultimátum. [Undergraduate thesis, Universidad Carlos III de Madrid]. https://e-archivo.uc3m.es/handle/10016/5838#preview
[6] Sanfey, A. (2007). Social Decision-Making: Insights from Game Theory and Neuroscience. Science, 318(5850), 598-602. doi: https://doi.org/10.1126/science.1142996
[7] De Jong, S., Uyttendaele, S. & Tuyls, K. (2008). Learning to reach agreement in a continuous ultimatum game. Journal of Artificial Intelligence Research, 33, 551-574. doi: https://doi.org/10.1613%2Fjair.2685