Análisis y evaluación de la eficiencia coseno de un colector cilindro parabólico polar: Aplicación en una región subtropical de Argentina
Analysis and evaluation of the cosine efficiency of a polar parabolic trough collector: Application in a subtropical region of Argentina
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
Recepción: 09 Mayo 2021
Aprobación: 31 Agosto 2021
Resumen: Se analiza el comportamiento de un dispositivo de concentración solar para la generación directa de vapor localizado en Ezeiza (34,82 S, 58,53 W) región subtropical de Argentina. El dispositivo consiste en un concentrador cilindro parabólico y un receptor con agua como fluido de trabajo, se conoce como colector cilindro parabólico polar porque está inclinado según la coordenada de latitud. Este colector es prometedor para sistemas que usan energía solar concentrada en latitudes subtropicales, porque aprovecha mejor el recurso solar para generar calor o electricidad, en aplicaciones de ingenierías mediana y baja escala. El colector tiene un eje de rotación longitudinal inclinado sobre la línea imaginaria norte-sur, el concentrador está curvado parabólicamente y realiza el seguimiento solar sobre su eje de rotación. Se analiza matemáticamente con datos de un año solar típico y se compara el colector cilindro parabólico polar con uno sin inclinación. Se encuentra que el colector cilindro parabólico polar muestra una mejora significativa en la eficiencia óptica coseno durante todo el año especialmente en el invierno, con una pérdida anual de la energía disponible debido al efecto coseno del 4% frente a una pérdida del 13% para el concentrador sin inclinar. Con el fin de eliminar las pérdidas por final del colector, se han calculado las dimensiones óptimas del receptor empleando el método Montecarlo, obteniéndose un receptor de 3,2 m que sobresale 0,4 m por encima y por debajo del concentrador. El área del receptor es un 10,6% mayor en el colector inclinado, para disminuir las pérdidas térmicas se propone un aislamiento térmico estacional.
Palabras clave: Energía Solar Concentrada, Colector Cilindro Parabólico, Generación Directa de Vapor, Región Subtropical.
Abstract: The behavior of a solar concentrating device for direct steam generation located in Ezeiza (34.82 S, 58.53 W) subtropical region of Argentina is analyzed. The device consists of a parabolic trough concentrator and a receiver with water as the working fluid; it is known as a polar parabolic trough collector because it is inclined according to the latitude coordinate. This collector is promising for systems that use concentrated solar energy in subtropical latitudes, because it makes better use of the solar resource to generate heat or electricity, in medium- and low-scale applications. The collector has a longitudinal axis of rotation inclined on the imaginary north-south line. The concentrator is parabolically curved and tracks the sun on its axis of rotation. It is mathematically analyzed with data from a typical solar year and the polar parabolic trough collector is compared with one without inclination. It is found that the polar parabolic trough collector shows a significant improvement in the optical cosine efficiency throughout the year, especially in winter, with an annual loss of available energy due to the cosine effect of 4% compared to a loss of 13% for the concentrator without tilting. In order to eliminate losses at the end of the collector, the optimal dimensions of the receiver have been calculated using the Monte Carlo method, obtaining a 3.2 m receiver that protrudes 0.4 m above and below the concentrator. The receiver area is 10.6% larger in the inclined collector. To reduce thermal losses, a seasonal thermal insulation is proposed.
Keywords: Concentrating Solar Power, Parabolic Trough Collector, Direct Steam Generation, Subtropical Region.
INTRODUCCIÓN
La demanda de energía crece continuamente a nivel global. Las predicciones indican que entre 2015 y 2040 el consumo mundial de energía aumentará en un 28% [1]. Los logros sociales y tecnológicos del siglo pasado fueron consecuencia del fácil acceso al petróleo, carbón y gas natural, cuyos procesos de oxidación han contribuido al aumento de la contaminación ambiental y a un peligroso calentamiento global.
La energía solar es una de las formas de energía alternativa con el potencial de suministrar el calor y la energía que demanda toda la población de la Tierra. Para obtener electricidad a partir de la energía solar, es posible aprovechar tanto el efecto fotovoltaico como el contenido de calor de los rayos solares [2, 3]. Esto último se logra con la ayuda de concentradores solares espejados que interceptan la luz solar y la reflejan en un receptor. Varios dispositivos termosolares están en desarrollo o ya se están aplicando para usos comerciales [4]. Uno de ellos es el llamado concentrador cilindro parabólico (CCP) que tiene un eje usualmente ubicado a lo largo de la línea imaginaria norte-sur. El CCP es capaz de concentrar la radiación solar en un receptor tubular ubicado en una zona de enfoque lineal. En el receptor, el agua que circula es calentada por los rayos solares concentrados produciendo vapor saturado o sobrecalentado, para ser utilizado posteriormente en procesos térmicos o para obtener electricidad [5].
Para lograr la concentración óptima de rayos solares en el concentrador es importante que el mismo esté orientado hacia Sol y siguiendo su movimiento aparente durante su funcionamiento, de lo contrario los rayos solares no se concentrarán adecuadamente en el tubo receptor [6]. Es importante definir dos parámetros solares para comprender el fenómeno de la concentración de radiación solar, uno es el plano de apertura del concentrador por el cual ingresan los rayos solares al mismo, el otro es el ángulo de incidencia solar (θ) que se forma entre el vector normal al plano de apertura y la ubicación del Sol. Cuando θ es distinto de cero, el flujo solar radiante que atraviese el plano de apertura se ve disminuido debido al llamado “efecto coseno”, definiendo una eficiencia coseno que varía entre 0 y 1, según el valor del cos θ [5].
Los CCPs que cuenten con seguimiento en eje norte-sur, alinearán la componente este- oeste de la normal del plano de apertura con la posición solar pero no podrán hacerlo en el sentido norte-sur, por lo que si el sol no se encuentra sobre el paralelo (línea este- oeste) existirá una disminución de la energía colectada debido al efecto coseno. Esta es la razón por la cual, la mejor ubicación para el CCP es sobre el ecuador terrestre, ya que es en esta región donde el Sol se encuentra más próximo por sobre el paralelo a lo largo del año, permitiendo tener así una mejor recolección de energía con eficiencias coseno más altas. En otras latitudes los CCPs lograrán eficiencias menores, efecto que se incrementa al aumentar la latitud. [7-9].
En regiones subtropicales el arco de la trayectoria solar nunca se encuentra por sobre el paralelo, por esto los sistemas CCPs tendrán una reducción de eficiencia significativa. Diversos autores han propuesto otros sistemas de seguimiento solar para mitigar esta dificultad [10, 11]. Así, el sistema de seguimiento polar que inclina el eje de rotación del colector tantos grados como la latitud del lugar (elevando el concentrador por su extremo norte en el hemisferio norte o por su extremo sur en el hemisferio sur) ha mostrado un buen desempeño en todas las latitudes. Este sistema es denominado colector cilindro parabólico polar (CCPP).
Se han realizado diferentes estudios para determinar el ángulo de inclinación óptimo del concentrador y así recolectar la cantidad máxima de energía anual. Zhang et al. calcularon mediante un algoritmo numérico estocástico los ángulos de inclinación óptimos para cinco ciudades chinas ubicadas en distintas latitudes [9]. Por otra parte, El Kassaby encontró que el ángulo de inclinación óptimo resulta de la suma del valor de la latitud local más 3.5° [7].
La elección de datos meteorológicos adecuados es fundamental para realizar una simulación energética y lograr conclusiones válidas. La variación de las condiciones ambientales más realista se logra mediante el uso de año meteorológico típico (AMT), que es un año estadístico que consta de 12 meses meteorológicos típicos basados en mediciones de campo que se extienden a lo largo de décadas [12].
Este trabajo tiene como objetivo demostrar que la elección de un colector cilindro parabólico inclinado según la latitud logra disminuir el ángulo de incidencia a lo largo del año, con respecto al colector no inclinado. Se propone analizar el efecto del ángulo de incidencia sobre la energía solar colectada utilizando un AMT para el CCP y el CCPP ubicados en el Aeropuerto de Ezeiza, Buenos Aires, así como determinar la longitud adecuada del receptor del CCPP para atenuar las pérdidas por final de colector.
METODOLOGÍA
El análisis es realizado para las coordenadas 34,82 S, 58,53 W, que coincide con el Aeropuerto de Ezeiza, Buenos Aires, Argentina, Fig. 1.
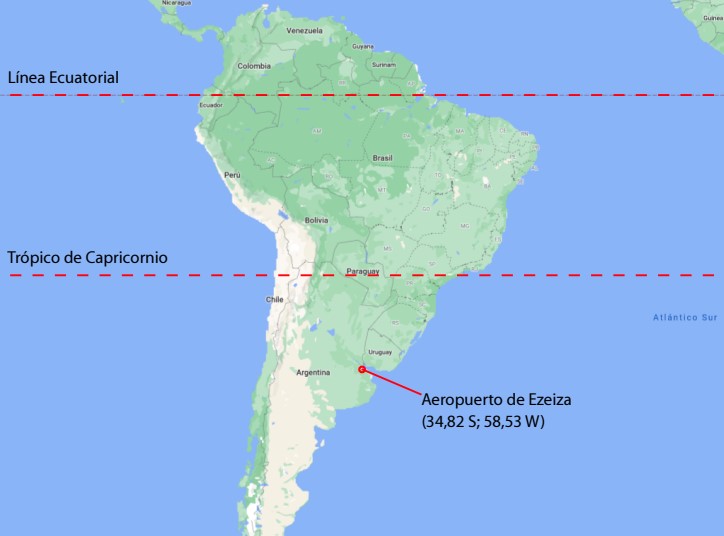
Figura 1
Ubicación del Colector Problema
En los colectores cilindro parabólicos todo el conjunto, concentrador y receptor, está montado sobre una estructura que sigue la trayectoria solar en el eje norte-sur durante el movimiento diurno. En la Fig. 2 se muestra un dispositivo CCP clásico y en la Fig. 3, se muestran las disposiciones de (a) un conjunto de CCPs ordenados en serie y (b) un conjunto de CCPPs ordenados en paralelo. Es importante señalar que para un pequeño campo solar en una región subtropical; es conveniente utilizar CCPPs más cortos para lograr una estabilidad estructural adecuada. En una ubicación subtropical, la elección de un CCPP se realiza para abordar dos dificultades encontradas en la generación directa de vapor utilizando CCP La primera se debe a la variabilidad del ángulo 0, lo que provoca el efecto coseno y por tanto una pérdida de la energía captada; la segunda dificultad es la generación de un flujo bifásico de agua / vapor en el receptor durante las horas alejadas del mediodía, cuando la radiación reflejada incide lateralmente y se produce un mal intercambio de calor entre las paredes del receptor caliente y el vapor, como se muestra en la Fig. 4 [13]. Independientemente de la suposición acerca de que la inclinación del sistema ayudará en gran medida a disminuir el flujo bifásico, este cambio de comportamiento del fluido dentro del receptor no se analizará en este trabajo, aunque está propuesto para futuras investigaciones.
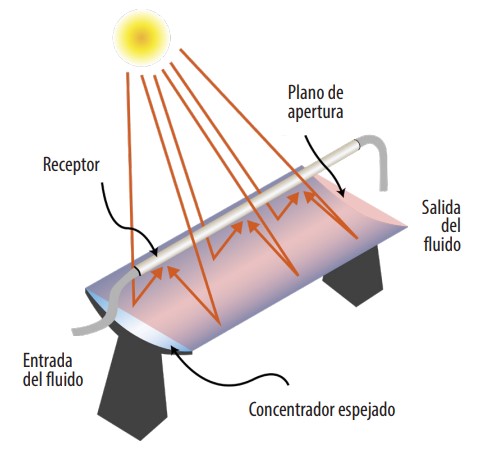
Figura 2
Diseño de un Dispositivo Clásico CCP
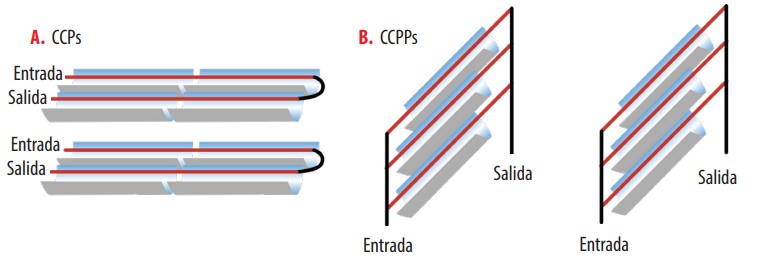
Figura 3
Diseño del Ordenamiento de los Conjuntos a) CCPs b) CCPPs
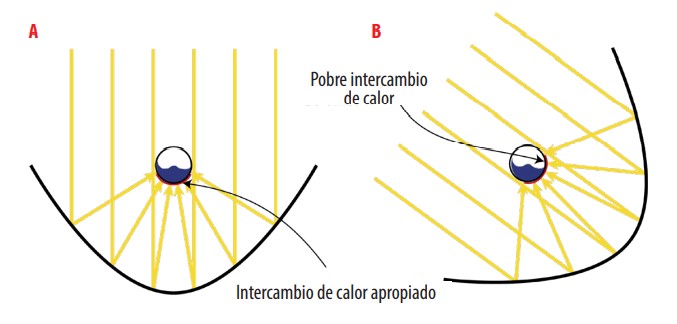
Figura 4
Intercambio de Calor en CCP: a) al Mediodía b) a la Mañana/a la Tarde
Evaluación del ángulo de incidencia solar (θ)
Para analizar el efecto de θ sobre la energía térmica captada, es necesario definir la fracción colectada (Cf ) como la relación entre la potencia (Pr) entregada por el concentrador al receptor por unidad de área del plano de apertura y la potencia proporcionada por el Sol por metro cuadrado (Ps) [5]:
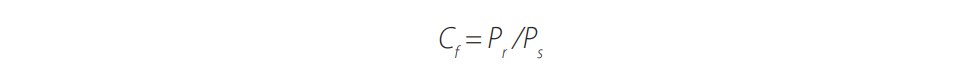 (1)
(1)Cf es 1, cuando el sistema está perfectamente alineado y todos los rayos incidentes se reflejan en el receptor (caso de espejos ideales).
Cuando θ es distinto de cero, Cf se modifica según [5]:
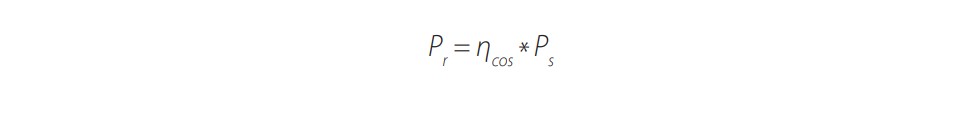 (2)
(2)donde ηcos se define como la eficiencia coseno o el modificador del ángulo de incidencia:
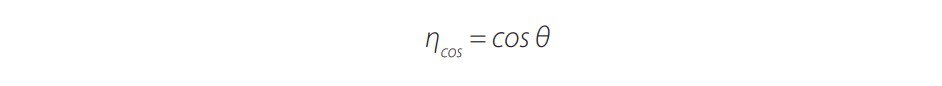 (3)
(3)Para ambos concentradores, CCPP y CCP, θ se puede calcular en cualquier momento utilizando el vector de posición solar U, que se determina utilizando el algoritmo de posicionamiento solar [14] y se representa como:
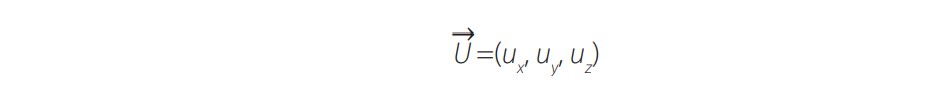 (4)
(4)
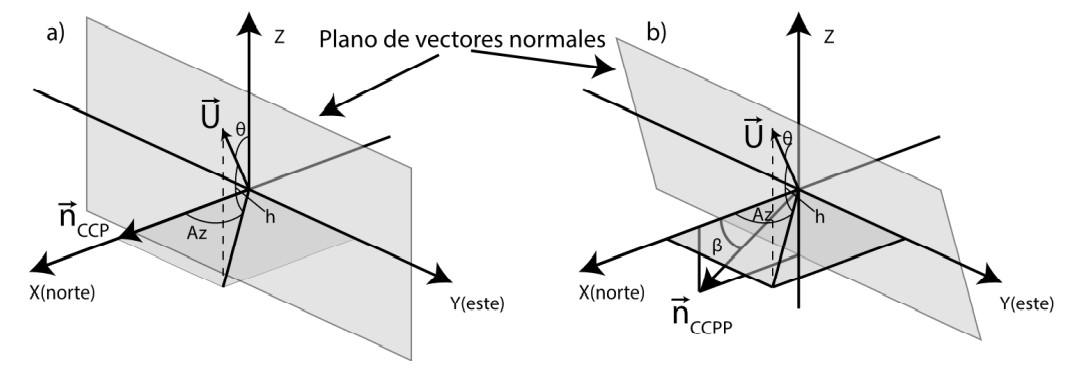
Firgura 5
Diagrama de Vectores a) para CCP y b) para CCPP. Az es el azimut y h es la elevación solar
Para obtener el valor θ se define otro vector k, unitario y paralelo al eje de rotación del colector. Como k es paralelo al eje de rotación, k también es perpendicular al plano que contiene todos los vectores normales al plano de apertura (puesto que el plano de apertura es orientado por el sistema de seguimiento para alinearse con el Sol). Para el CCP, el vector k que se muestra en la Fig. 5a, se puede escribir como:
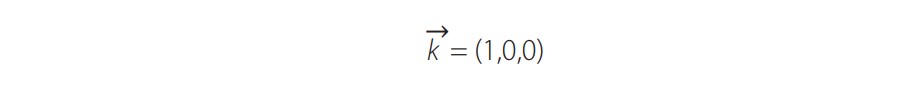 (5)
(5)Debido a su eje de rotación, k está alineado con el meridiano local y colocado horizontalmente, mientras que en la Fig. 5b, para CCPP el vector es:
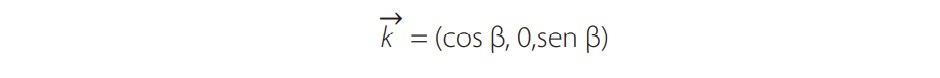 (6)
(6)Donde β es el ángulo de inclinación del concentrador. En consecuencia, los valores de θ se determinan para todos los k vectores de acuerdo con:
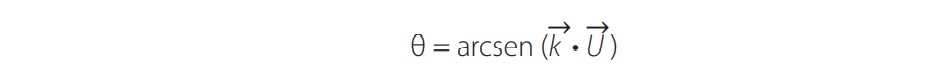 (7)
(7)El algoritmo de posicionamiento solar se utiliza para calcular U para todo el año tomando una hora como intervalo de tiempo. Como las condiciones ambientales (radiación solar incidente, temperatura, humedad, etc.) varían significativamente de un año a otro, no se pueden obtener resultados confiables usando parámetros medidos en solo un año calendario. Resulta apropiado aplicar el AMT.
En el algoritmo, además de los datos de posicionamiento (latitud, longitud y altitud), se ingresaron los de humedad, presión atmosférica y temperatura del AMT, en el Aeropuerto de Ezeiza [12]. Usando el conjunto de datos 0 para cada vector k, se calcula un conjunto de datos de cos0. Además, los valores de Pr se obtienen usando la Ecuación 2, tomando los valores de Ps del AMT. Con esta colección de datos se realiza una integración trapezoidal de la potencia solar colectada Pr para cada sistema y se compara la energía solar captada anualmente con las configuraciones CCPP y CCP.
Optimización del tubo receptor del CCPP
En todos los concentradores cilindro parabólicos existe una disminución de la eficiencia debido a la pérdida los extremos del concentrador, que ocurre cuando la radiación que ha incidido en el extremo del espejo se refleja fuera del receptor Fig. 6. Xu et.al sugirieron reducir las pérdidas por un método de compensación aplicable en regiones con una latitud superior a 25° [15].
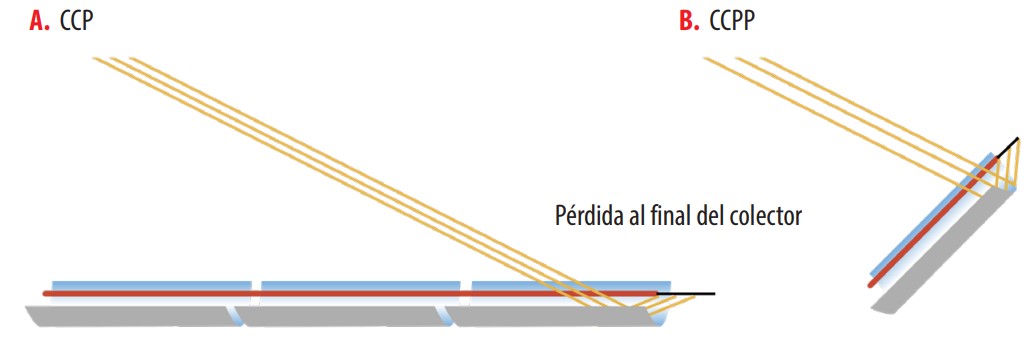
Figura 6
Pérdidas al Final del Concentrador a) CCP y b) CCPP
Para optimizar el tamaño del tubo receptor del CCPP, el software Tonatiuh Ray Tracing realiza una simulación óptica que utiliza el método de Monte Carlo para endone modelar el camino de un gran conjunto de elementos aleatorios que actúan como fotones emitidos por el sol [16]. El software permite seleccionar los parámetros del concentrador y su orientación espacial. Se trabaja con un concentrador de 2,40 m de largo y 3,00 m de ancho. La distancia focal se establece en 0,90 m, medida desde el vértice de la parábola. Para trabajar con un modelo realista, la reflectividad de la superficie se fija en 0,85 y el a de pendiente en 3 mrad, de acuerdo con un espejo real de cristal promedio [11, 17, 18].
Para la simulación, se ubica en el área focal del concentrador un objetivo que consiste en un plano rectangular de 4,00 m de largo y 0,20 m de ancho con su lado más largo siguiendo la línea focal. El objetivo se utiliza para analizar el ancho y la longitud del área focal porque, de esta forma, es más fácil elegir un diámetro para el tubo receptor. En la simulación, se escoge una cantidad de 5 x 107 fotones. Para representar correctamente el Sol, se utiliza una distribución pillbox. Los fotones impactan primero en la superficie del concentrador, luego son reflejados, y finalmente chocan con el objetivo. El software genera un archivo de datos binarios con las coordenadas de cada colisión que luego se procesan utilizando diferentes algoritmos. Para medir la concentración local de fotones que impactan en el objetivo, se construye en el mismo una malla de 1000 x 1000 celdas y se cuenta el número total de fotones que chocan en cada una de ellas. Se excluye la zona difusa, considerando solo el área de mayor intensidad que contiene 88,5 % de los fotones impactados en el objetivo.
Para analizar el comportamiento del concentrador en la ubicación 34,82 S, 58,53 W (Aeropuerto de Ezeiza), se seleccionan tres posiciones que representan el 0 máximo y el 0 mínimo i) solsticio de verano, θ= 22,41°, ii) equinoccios de primavera y otoño θ = 0°, y iii) solsticio de invierno θ= -22,41°. Los valores de θ se consideran constantes durante los días seleccionados.
RESULTADO Y DISCUSIÓN
Análisis comparativo de concentradores CCP y CCPP
Para CCPP la variación diaria de θ, durante los solsticios, es 0,23° y durante los equinoccios 0,38°. Los valores promedio de la variación diaria de θ para ambos colectores se muestran en la Tabla 1. Los valores de θ son casi constantes a lo largo del día con un CCPP, mientras que con un CCP la variación diaria es mucho mayor. Las variaciones medias mensuales de θ para ambos concentradores se muestran en la Fig. 7.

Comparación de Resultados entre el CCP y el CCPP
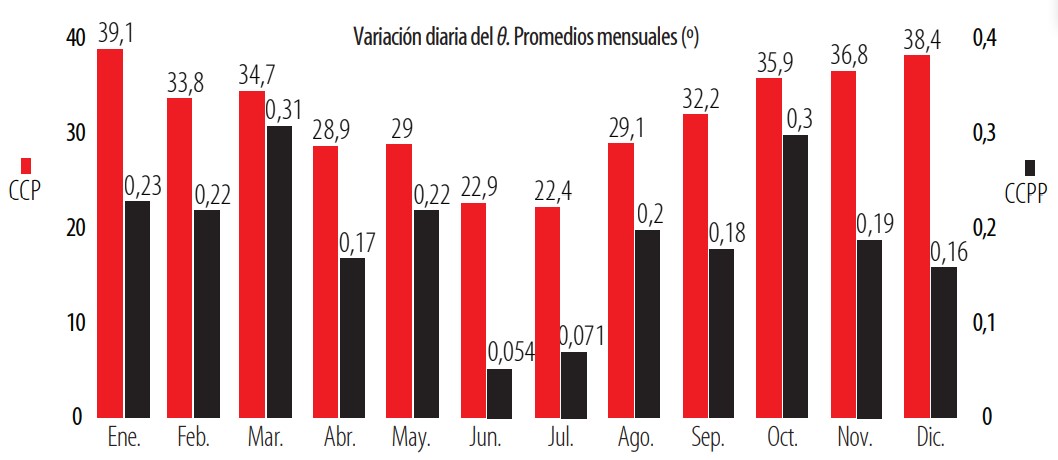
Figura 7
Variación Diaria de 0 en Promedios Mensuales de un AMT. En azul para CCP y en naranja para CCPP.
Esta variación diaria de θ indica la estabilidad del sistema para recolectar energía. Los valores pequeños de este parámetro tendrán la misma eficiencia coseno durante todo el día para el concentrador; consecuentemente, existirá una captación de energía proporcional a la energía solar accesible.
La Fig. 8 muestra θpara CCP y CCPP durante todo el año. Para que el gráfico sea más comprensible, se han añadido los recuadros con los valores de θ correspondientes a los solsticios y los equinoccios de otoño y primavera.
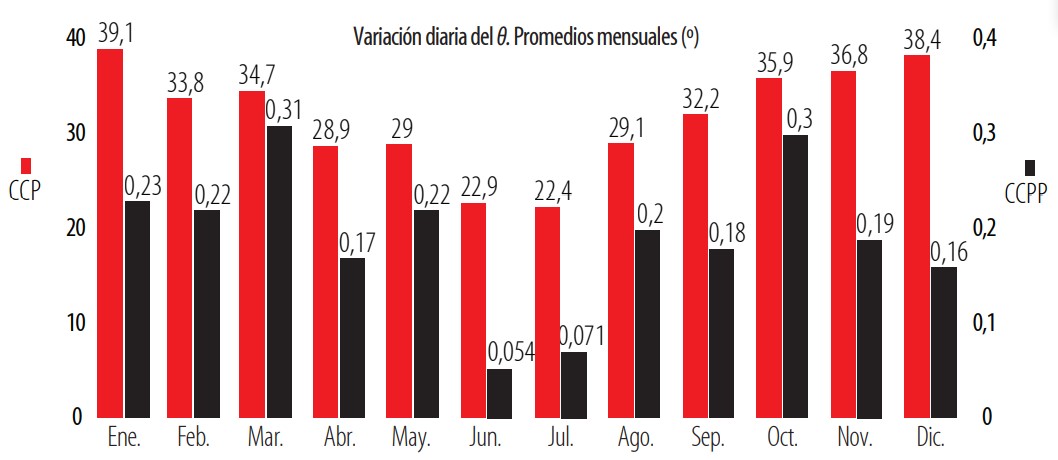
Figura 8
Variación de 0 a lo largo del Año. En azul para CCP y en naranja para CCPP. Los recuadros muestran el aumento de un día en el gráfico en a) equinoccio de otoño, b) solsticio de invierno, c) equinoccio de primavera y d) solsticio de verano.
Con los valores de θ obtenidos a lo largo del año, pueden calcularse los de ncos que se representan en la Fig. 9 en función del tiempo para CCP y CCPP.
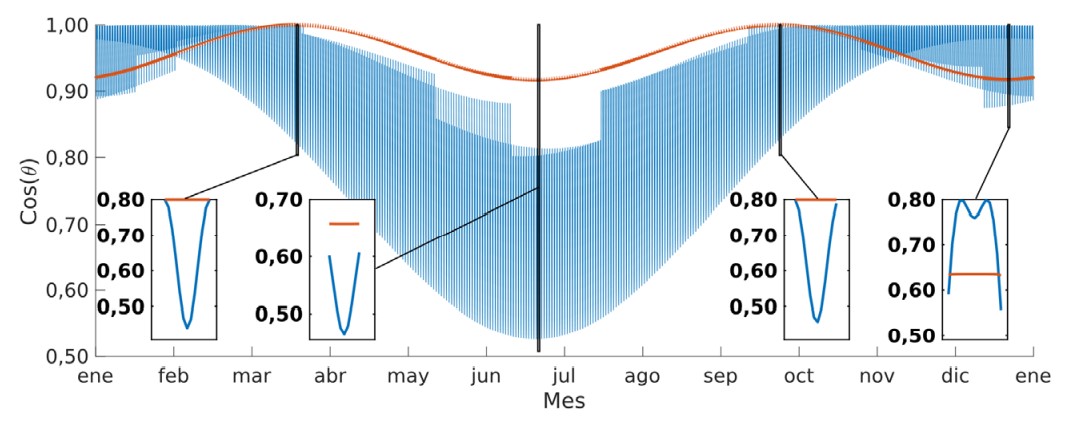
Figura 9
Variación de cos0 a lo largo del Año. En azul para CCP y en naranja para CCPP. Los recuadros muestran la variación en a) equinoccio de otoño, b) solsticio de invierno, c) equinoccio de primavera y d) solsticio de verano.
Se observa una gran estabilidad durante todo el año en los valores de ncos para el CCPP, mientras que existe, para el mismo intervalo, una marcada variación de ncos para el CCP De acuerdo con la Ec. 2, los valores más cercanos a 1 implicarán una mejor recolección de energía. Además, los valores de ncos para el CCPP varían entre 0,92 y 1,00, mientras que para el CCP varían entre 0,50 y 1,00.
Para analizar el efecto de ncos en P se puede calcular Pr para CCP y CCPP para cada momento del año aplicando la Ec. 2, los datos de Ps son obtenidos del AMT del Aeropuerto Nacional de Ezeiza, Argentina. Los resultados se muestran en la Fig. 10.
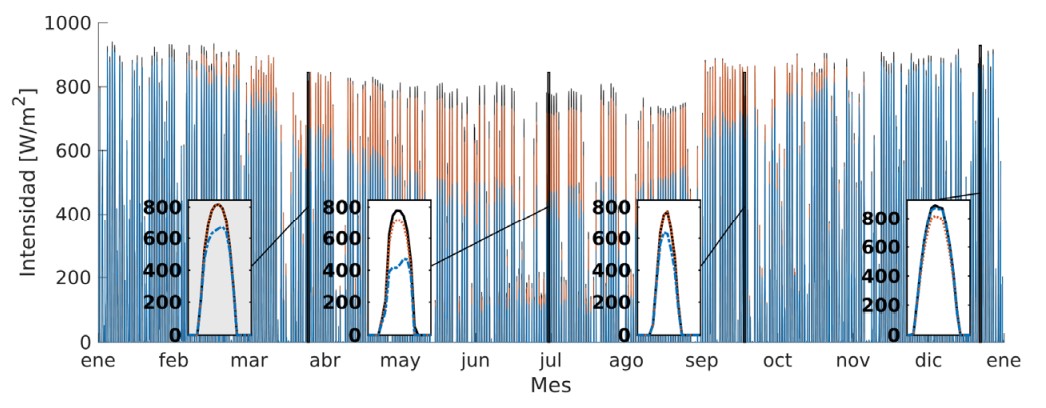
Figura 10
Variaciones de PS (negro) y Pr (en naranja para CCPP, en azul para CCP) durante todo el año. Los recuadros (ampliar para ver detalle) muestran la variación en a) equinoccio de otoño, b) solsticio de invierno, c) equinoccio de primavera y d) solsticio de verano.
Realizando una integración trapezoidal de los valores de Pr a lo largo del año, la cantidad total de energía obtenida es 1,40 MJm-2 para CCPP y 1,28 MJm-2 para CCP. Con la integración trapezoidal anual de Ps (1,47MJm-2) es posible determinar la eficiencia coseno para ambos colectores, que resulta ser 0,96 para CCPP y 0,87 para CCP. Estos valores se muestran en la Tabla 1.
Además del aumento en la eficiencia, el CCPP muestra una captación de energía estable a lo largo de los días y del año. Para CCP, en cambio, se observan grandes variaciones de la energía recolectada, tanto diaria como estacional, con una notable disminución en el rendimiento durante el invierno, Fig. 10. Estos resultados justifican recomendar el uso de sistemas CCPP en regiones subtropicales.
En este trabajo se obtuvieron resultados comparables con otros publicados. El Kassaby obtuvo para una latitud similar (35°) un ncos anual de 0.934 para un CCPP y de 0.78 para un CPP [7], mientras que Zhang et al. obtuvieron un ncos anual estimado de 0.93 para un colector inclinado con la latitud [9]. Los valores informados en este estudio son más cercanos a la realidad porque se contemplan los días nublados al utilizar datos del AMT, que dan valores de Ps más bajos que los utilizados por los otros autores, obteniéndose en consecuencia una mayor eficiencia anual.
Optimización del tubo receptor con CCPP
A pesar que el CCPP tiende a disminuir el ángulo de incidencia debido a la latitud del emplazamiento, se observa que las dimensiones del receptor deben ser modificadas en referencia a las del receptor del CCP.
Para determinar las dimensiones del receptor, es necesario considerar no solo la longitud sino también el ancho del área focal. Aplicando el método Monte Carlo se obtienen los siguientes resultados i) en el solsticio de verano: la imagen focal se extiende 0,40 m por debajo del colector, ver Fig. 11a); ii) en los equinoccios: la imagen focal se extiende desde el principio hasta el final del colector, ver Fig. 11b); iii) en el solsticio de invierno: la imagen focal se extiende 0,40 m por encima del colector, ver Fig. 11c).
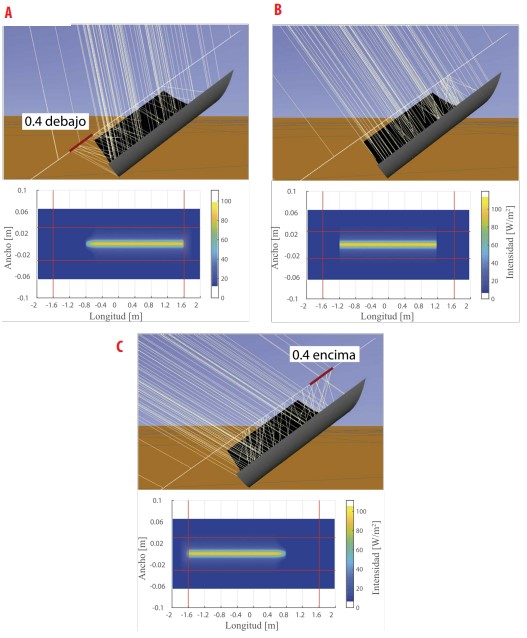
Figura 11
Trazado de Rayos para CCPP. El inicio y el final del receptor propuesto se muestran en líneas rojas verticales, el ancho de la franja focal con 88,5% de la energía reflejada se muestra en la línea roja horizontal a) durante el solsticio de verano, e y c) durante los equinoccios.
Se ha obtenido un ancho de 0,051 m para los equinoccios, y casi el mismo valor para los solsticios, 0,052 m. Por lo tanto, el receptor propuesto tiene un diámetro de 0,052m y una longitud de 3,20 m con 0,40 m por encima y por debajo de la longitud del concentrador.
Según el mismo análisis para un CCP con una longitud de 2,4 m, el diámetro calculado del receptor es 0,062 m. Se observa que el área del receptor para CCPP es 10,6% mayor que la de CCP.
Para atenuar posibles pérdidas térmicas, se propone el aislamiento del final del receptor que no esté en uso (es decir, el extremo inferior en el lapso de tiempo que va desde el equinoccio de primavera al equinoccio de otoño; y el extremo superior en el lapso de tiempo que va desde del equinoccio de otoño al equinoccio de primavera).
CONCLUSIONES
El análisis teórico realizado en este trabajo permite distinguir el comportamiento del CCPP de aquel del clásico colector solar CCP para la región de Ezeiza, Argentina.
El dispositivo CCPP tiene dos importantes logros a destacar:
El primero es la reducción del efecto coseno, que muestra una mejora del ncos durante todo el año en la latitud seleccionada, (anualmente fue de 0,87 en CCP y de 0,96 en CCPP).
El segundo logro es que las variaciones diarias de θ son casi insignificantes para CCPP lo que aumenta la estabilidad del sistema. Ambos logros dependen de la latitud: cuanto más lejos del ecuador, más importantes resultan éstos.
El CCPP presenta un rendimiento superior especialmente en invierno, donde el CCP tiene mayores variaciones de θ y en consecuencia un ncos menor.
Para reducir las pérdidas por final de colector en el extremo del CCPP se debe seleccionar un tubo receptor más largo que el propuesto para CCP. Aunque este receptor es más largo, también es más delgado, lo que resulta en un aumento en el área de superficie de solo 10,6%.
Con el receptor más largo, las pérdidas térmicas del tubo receptor se pueden mitigar con aislamiento térmico estacional.
El uso de CCPP es promisorio para su aplicación en latitudes subtropicales y proporciona un mejor aprovechamiento del recurso solar, especialmente en aplicaciones de mediana y pequeña escala, para los procesos involucrados en la obtención de calor o generación de electricidad.
AGRADECIMIENTOS
Este trabajo fue financiado por la Comisión de Investigaciones Científicas de la Provincia de Buenos Aires (CICPBA), Proyecto de innovación y Transferencia en Áreas Prioritarias de la Provincia de Buenos Aires (PIT-AP-BA) 2016/2017 y Universidad Tecnológica Nacional (UTN-FRLP). DP agradece el apoyo financiero de una beca doctoral CICPBA. AMCL es miembro de la carrera de Investigador Científico CICPBA
CONTRIBUCIONES DE LOS AUTORES
Dario H. Panaroni y Luis C. Martorelli concibieron la investigación y diseñaron la metodología; Dario H. Panaroni y Ana M. Castro Luna se encargaron de la curación de datos para la investigación, adquisición, análisis e interpretación de los datos, además redactaron y revisaron el manuscrito.
CONFLICTO DE INTERÉS
Los autores declaran que esta investigación fue conducida en la ausencia de relaciones comerciales o financieras que pudieran constituir un potencial conflicto de interés.
Referencias
Energy Agency, I. (2017). World Energy Outlook 2017. Organisation for Economic Cooperation and Development. https://doi.org/10.1787/weo-2017-en
Michaelides, E. E. (2012). Alternative Energy Sources. En Green Energy and Technology. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-20951-2
Höök, M., & Tang, X. (2013). Depletion of fossil fuels and anthropogenic climate change—A review. Energy Policy, 52, 797-809. https://doi.org/10.1016/j.enpol.2012.10.046
Fernández-García, A., Zarza, E., Valenzuela, L., & Pérez, M. (2010). Parabolic-trough solar collectors and their applications. Renewable and Sustainable Energy Reviews, 14(7), 1695-1721. https://doi.org/10.1016/J.RSER.2010.03.012
Lovegrove, K., & Stein, W. (2012). Concentrating solar power technology : principles, developments and applications (K. Lovegrove & W. Stein (eds.)). Woodhead Publishing. https://www.elsevier.com/books/concentrating-solar-power-technology/lovegrove/978-1-84569-769-3
Kumar, A., Chand, S., & Umrao, O. P. (2013). Selection and evaluation of different tracking modes performance for parabolic trough solar collector. International Journal of Engineering Research & Technology, 2(6), 2758-2764. https://www.ijert.org/selection-and-evaluation-of-different-tracking-modes-performance-for-parabolic-trough-solar-collector
El-Kassaby, M. M. (1994). Prediction of optimum tilt angle for parabolic trough with the long axis in the north-south direction. International Journal of Solar Energy, 16(2), 99-109. https://doi.org/10.1080/01425919408914269
Vician, P., Palacka, M., Durcansky, P., & Jandacka, J. (2017). Determination of Optimal Position of Solar Trough Collector. Procedia Engineering, 192, 941-946. https://doi.org/10.1016/j.proeng.2017.06.162
Zhang, Y., Qiu, Z. Z., Li, P., Guo, W., Li, Q., & He, J. (2013). Calculating the optimum tilt angle for parabolic solar trough concentrator with the north-south tilt tracking mode. Proceedings - 2013 4th International Conference on Digital Manufacturing and Automation, 2013, 329-334. https://doi.org/10.1109/ICDMA.2013.405
J. Daghero, J. Garnica, A. Buitrago, D. Dubini, C. Lorenzo, C. Manero, M. Marticorena, M., & Martinez, U. S. (2015). Concentrador cilindrico parabólico aplicado a la generación de vapor de uso industrial. Evaluación óptica y térmica de un prototipo. Avances en Energías Renovables y Medio Ambiente, 19, 45-54. http://portalderevistas.unsa.edu.ar/ojs/index.php/averma/article/view/1762
Xu, E., Zhao, D., Xu, H., Li, S., Zhang, Z., Wang, Z., & Wang, Z. (2015). The Badaling 1MW Parabolic Trough Solar Thermal Power Pilot Plant. Energy Procedia, 69, 1471-1478. https://doi.org/10.1016/j.egypro.2015.03.096
Bre, F., & Fachinotti, V. D. (2016). Generation of typical meteorological years for the Argentine Littoral Region. Energy and Buildings, 129, 432-444. https://doi.org/10.1016/j.enbuild.2016.08.006
Zarza Moya, E. (2003). Generación directa de vapor con colectores solares cilindro parabólicos. Proyecto Direct Solar Steam (DISS). http://www.tdx.cat/handle/10803/114351
Reda, I., & Andreas, A. (2004). Solar position algorithm for solar radiation applications. Solar Energy, 76(5), 577-589. https://doi.org/10.1016/j.solener.2003.12.003
Xu, C., Chen, Z., Li, M., Zhang, P., Ji, X., Luo, X., & Liu, J. (2014). Research on the compensation of the end loss effect for parabolic trough solar collectors. Applied Energy, 115, 128-139. https://doi.org/10.1016/j.apenergy.2013.11.003
Blanco, M. J., Amieva, J. M., & Mancillas, A. (2005). The Tonatiuh Software Development Project: An Open Source Approach to the Simulation of Solar Concentrating Systems. Computers and Information in Engineering, 2005, 157164. https://doi.org/10.1115/IMECE2005-81859
Giglio, A., Lanzini, A., Leone, P., Rodríguez García, M. M., & Zarza Moya, E. (2017). Direct steam generation in parabolic-trough collectors: A review about the technology and a thermo-economic analysis of a hybrid system. Renewable and Sustainable Energy Reviews, 74(March 2016), 453-473. https://doi.org/10.1016/j.rser.2017.01.176
Krüger, D., Pandian, Y., Hennecke, K., & Schmitz, M. (2008). Parabolic trough collector testing in the frame of the REACt project. Desalination, 220(1-3), 612-618. https://doi.org/10.1016/j.desal.2007.04.062