Relación cuantitativa estructura actividad del factor de bioconcentración de los bifenilos policlorados en especies de peces utilizando métodos basados en aprendizaje de máquina
Quantitative structure activity relationship of bioconcentration factor of polychlorinated biphenyls in fish species using machine learning
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
Recepción: 08 Mayo 2021
Aprobación: 15 Septiembre 2021
Resumen: Los bifenilos policlorados (PCBs) son contaminantes persistentes que afectan enormemente a los ecosistemas marinos. Utilizando técnicas de aprendizaje de máquina, se construyeron modelos de relación cuantitativa estructura-actividad (RCEA) para predecir el factor de bioconcentración (BCF) de los PCBs. Estos modelos se construyeron a partir de descriptores topográficos 2D y 3D calculados para la estructura molecular optimizada en el nivel de mecánica molecular. Después de analizar sus parámetros estadísticos, se determinó que dos modelos son bastante robustos para la predicción de logBCF. Los modelos seleccionados fueron: M_4_LR construido con dos descriptores moleculares y presenta valores de R2 = 0,9154, Q2 LOO= 0,8944, y Q2 ext= 0,9119, y M_13 construido con cuatro descriptores moleculares y presenta valores de R2 = 0,9375, Q2 LOO= 0,9155, y Q2 ext= 0,844. Los dos modelos pasaron la doble fase de validación y cumplieron con los criterios de la prueba de Tropsha. Esto implica que las predicciones para el logBCF fueron bastante precisas tal como se muestra en los resultados del presente estudio.
Palabras clave: Regresión lineal, PCBs, descriptores moleculares, mecánica molecular, especies marinas.
Abstract: Polychlorinated biphenyls (PCBs) are persistent pollutants that greatly affect marine ecosystems. Machine learning techniques were used to build quantitative structure activity-relationship (QSAR) models that predict PCBs’ bioconcentration factor (BCF). These models were built from topographic 2D and 3D descriptors calculated for the molecular structures optimized at molecular mechanics level of theory. After analyzing their statistical parameters, it was determined that two models are robust enough for predicting logBCF. The selected models were: M_4_LR, built with two molecular descriptors and showed values of R2= 0,9154, Q2LOO= 0,8944, y Q2ext= 0,9119, and M_13, built with four molecular descriptors and showed values of R2= 0,9375, Q2LOO= 0,9155, y Q2ext= 0,844. Both models passed the double validation phase, and they satisfied the criteria from Tropsha’s test. This implies that predictions for logBCF were quite accurate, as is showed in the results from the present study.
Keywords: Linear regression, PCBs, molecular descriptors, molecular mechanics, marine species.
INTRODUCCIÓN
En los últimos años, los bifenilos policlorados (PCBs) han sido estudiados por los investigadores debido a sus repercusiones negativas en la salud debido a su incremento acelerado en el ambiente [1-3]. Los PCBs son un grupo de contaminantes orgánicos cuya estabilidad fisicoquímica les permiten resistir en el medio ambiente por un largo tiempo incluso en diferentes condiciones ambientales [3-8]. A pesar de que estos compuestos han sido sujetos a prohibiciones en muchos países debido a sus efectos adversos, los PCBs siguen presentes en los ecosistemas acuáticos [1,5,9-12]. La naturaleza hidrofóbica de los PCBs les permite sedimentar y formar reservorios en las profundidades de los cuerpos de agua donde se encuentran las poblaciones de corales, por esta razón, algunas especies de peces consumen directamente estos químicos [5,12]. En consecuencia, la cadena alimenticia submarina se ve afectada, y las personas se exponen a estos compuestos tóxicos principalmente mediante el consumo de especies acuáticas [1,9,12]. Después de la ingestión, los PCBs tienden a acumularse en los tejidos adiposos, y esto conlleva riesgos carcinógenos, reproductivos y genéticos [8,10,12]. Los PCBs son un problema tanto para los ecosistemas marinos como para la población mundial, por lo tanto, es de gran importancia estudiar la bioconcentración de los mismos.
La bioconcentración es la capacidad de un individuo de acumular una sustancia del ecosistema en sus tejidos [13-15]. En general, se puede cuantificar esta propiedad a través del factor de bioconcentración (BCF). El BCF es la proporción entre la concentración de un contaminante en la especie y la concentración del contaminante en el ambiente [16]. Este parámetro es de gran importancia para evaluar el riesgo potencial de un compuesto tóxico [8].
Los estudios de bioconcentración en especies acuáticas se realizan con el objetivo de extraer información sobre la cantidad de componentes tóxicos del agua que puede absorber directamente un organismo [17]. Sin embargo, la determinación del BCF a través de procedimientos experimentales presenta costos altos en cuanto a tiempo y dinero [4,8,11]. En consecuencia, algunos estudios teóricos han sido llevados a cabo para predecir características toxicológicas de las moléculas a través de modelos de relación cuantitativa estructura-actividad (RCEA)[2].
RCEA es una técnica muy utilizada para establecer relaciones entre las propiedades fisicoquímicas de sustancias y sus respectivas actividades biológicas [18]. El objetivo principal de un estudio RCEA es desarrollar modelos matemáticos utilizando descriptores moleculares para predecir propiedades biológicas de interés [19]. Los descriptores moleculares son representaciones matemáticas de una molécula obtenidos a partir de su estructura, a través de algoritmos computacionales [20]. Estos descriptores se clasifican en: una dimensión (1D), dos dimensiones (2D), y tres dimensiones (3D) de acuerdo con la complejidad de la estructura molecular optimizada [20]. Además, los descriptores se pueden calcular para diferentes niveles de teoría, siendo los métodos de mecánica molecular los que requieren menor cantidad de recursos computacionales [21].
La mecánica molecular (MM) es un nivel de teoría en el que una molécula se aproxima al comportamiento que tendrían bolas unidas por resortes [22]. El principio fundamental de la MM es expresar la energía potencial de una molécula en función de los términos que corresponden al estiramiento de enlaces, al doblamiento de los ángulos de enlace, a los ángulos diedros, y a las interacciones no enlazantes [22]. En general, las aproximaciones de la MM son bastante buenas para la obtención de energías con los parámetros adecuados; sin embargo, debido a que los cálculos se realizan en el estado basal de las moléculas, las geometrías no se adaptan bien cuando se estudian mecanismos en donde se involucran el rompimiento y la formación de enlaces [21].
En el presente trabajo, se presenta un estudio que se enfoca en la posible correlación que existe entre la estructura de los bifenilos policlorados y el factor de bioconcentración de estos compuestos en especies de peces. Para cumplir con este objetivo, se utilizaron descriptores topográficos 2D y 3D obtenidos a partir de las estructuras optimizadas en el nivel MM, y algoritmos de aprendizaje de máquina para la búsqueda de los posibles modelos. Estos modelos se validaron estadísticamente con la intención de evaluar la capacidad predictiva que presentan los mismos.
MATERIALES Y MÉTODOS
Preparación de los datos
Un conjunto de 58 compuestos cuya estructura se muestra en la Figura 1 fue utilizado para el modelaje realizado en el presente estudio. Las diferencias presentes en las estructuras en términos de la cantidad y posición de átomos de cloro se encuentran enlistadas en la Tabla 1 [11]. Una vez hecho esto, se representaron las estructuras moleculares 3D y 2D. Las estructuras 3D de las moléculas se optimizaron en el nivel de teoría de UFF (Universal Force Field), empleando el programa RDKit [23]. Posteriormente, se calcularon 89 descriptores 3D y 791 descriptores 2D con el software QuBiLS-MIDAS y QuBiLs-MAS, respectivamente [24]. Los valores para el logBCFexperimental se obtuvieron de la literatura para especies variadas de peces (guppies, pececillo de cabeza gorda, trucha arcoíris y pez luna de agallas azules) [25-32]. Finalmente, se empezó el modelado utilizando Weka 3.8.0 y MATLAB R2017b [33,34].
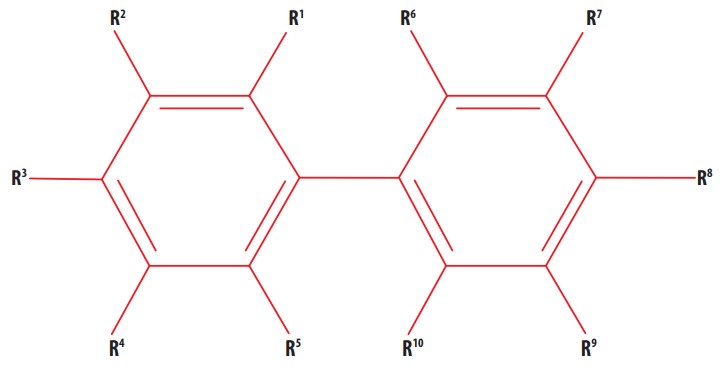
Figura 1
Estructura general para el bifenilo y sus derivados clorados.
| S.N. | CAS NO | Rn con Cl | logBCFexp |
| 1 | 92-52-4 | - | 2,64 |
| 2 | 2051-62-9 | R3 | 2,77 |
| 3 | 13029-08-8 | R1,R6 | 3,38 |
| 4 | 16605-91-7 | R1,R2 | 4,11 |
| 5 | 25569-80-6 | R^R2 | 3,8 |
| 6 | 33284-50-3 | R1,R3 | 3,55 |
| 7 | 34883-43-7 | R',R8 | 3,57 |
| 8 | 34883-39-1 | R1,R4 | 3,89 |
| 9 | 34883-41-5 | R2,R4 | 3,78 |
| 10 | 2050-68-2 | R3,R8 | 3,28 |
| 11 | 37680-65-2 | R1,R4,R6 | 4,11 |
| 12 | 7012-37-5 | R1,R3,R8 | 4,2 |
| 13 | 15862-07-4 | R1,R3,R5 | 4,26 |
| 14 | 16606-02-3 | R1,R4,R8 | 4,23 |
| 15 | 38444-93-8 | R1,R2,R5,R6 | 4,23 |
Compuestos de estudio junto su numeración (S.N), CAS, radicales sustituidos con cloro, y BCF experimental.
| aci avances enriendare ingenierías | S.N. | CAS NO | Rn con Cl | logBCFexp |
| 16 | 41464-39-5 | R1,R2,R6,R10 | 4,84 | |
| 17 | 2437-79-8 | R1,R3,R6,R8 | 4,85 | |
| 18 | 70362-47-9 | R1,R3,R4,R6 | 5 | |
| 19 | 41464-40-8 | R1,R3,R6,R9 | 4,84 | |
| 20 | 35693-99-3 | R1,R4,R6,R9 | 4,63 | |
| 21 | 15968-05-5 | R1,R5,R6,R10 | 3,85 | |
| 22 | 52663-58-8 | R1,R2,R5,R8 | 4,6 | |
| 23 | 32598-11-1 | R’.RXR* | 4,77 | |
| 24 | 32598-13-3 | R2,R3,R7,R8 | 4,59 | |
| 25 | 38380-02-8 | R1,R2,R3,R6 | 5,38 | |
| 26 | 68194-07-0 | R1,R2,R4,R6,R8 | 5 | |
| 27 | 41464-51-1 | R1,R3,R4,R6,R7 | 5,43 | |
| 28 | 38380-01-7 | R1,R3,R4,R6,R8 | 5 | |
| 29 | 37680-73-2 | R1,R3,R4,R6,R9 | 5,4 | |
| 30 | 32598-14-4 | R1,R2,R3,R7,R8 | 5 | |
| 31 | 74472-35-8 | R1,R2,R3,R5,R7 | 5 | |
| 32 | 31508-00-6 | R1,R3,R4,R7,R8 | 5 | |
| 33 | 57465-28-8 | R2,R3,R4,R/,R8 | 5,81 | |
| 34 | 38380-07-3 | R1,R2,R3,R6,R7,R8 | 5,77 | |
| 35 | 38411-22-2 | R1,R2,R5,R6,R7,R10 | 5,43 | |
| 36 | 35694-06-5 | R1,R2,R3,R4,R6,R8 | 5,88 | |
| 37 | 35065-28-2 | R1,R2,R3,R6,R8,R9 | 5,39 | |
| 38 | 52712-04-6 | R1,R2,R3,R4,R6,R9 | 5,81 | |
| 39 | 74472-41-6 | R1,R2,R4,R6,R8,R10 | 5,39 | |
| 40 | 52663-63-5 | R1,R2,R4,R5,R6,R9 | 5,54 | |
| 41 | 35065-27-1 | R1,R3,R4,R6,R8,R9 | 5,65 | |
| 42 | 33979-03-2 | R1,R3,R5,R6,R8,R10 | 4,93 | |
| 43 | 38380-08-4 | R1,R2,R3,R4,R7,R8 | 5,39 | |
| 44 | 69782-90-7 | R1,R2,R3,R7,R8,R9 | 5,39 | |
| 45 | 32774-16-6 | R2,R3,R4,R7,R8,R9 | 5,97 |
Continuación
| aci avances enriendare ingenierías | S.N. | CAS NO | Rn con Cl | logBCFexp |
| 46 | 38411-25-5 | R1,R2,R3,R4,R6,R7,R10 | 5,8 | |
| 47 | 35065-29-3 | R1,R2,R3,R4,R6,R8,R9 | 5,8 | |
| 48 | 60145-23-5 | R1,R2,R3,R4,R6,R8,R10 | 5,8 | |
| 49 | 52663-69-1 | R1,R2,R3,R5,R6,R8,R9 | 5,84 | |
| 50 | 52663-68-0 | R1,R2,R3,R5,R8,R9,R10 | 5,8 | |
| 51 | 74472-50-7 | R1,R2,R3,R5,R6,R7,R8 | 5,84 | |
| 52 | 35694-08-7 | R1,R2,R3,R4,R6,R7,R8,R9 | 5,81 | |
| 53 | 52663-78-2 | R1,R2,R3,R4,R5,R6,R7,R8 | 5,92 | |
| 54 | 42740-50-1 | R1,R2,R3,R4,R6,R7,R8,R10 | 5,92 | |
| 55 | 68194-17-2 | R1,R2,R3,R4,R5,R6,R7,R9 | 5,88 | |
| 56 | 2136-99-4 | R1,R2,R4,R5,R6,R7,R9,R10 | 5,82 | |
| 57 | 52663-77-1 | R1,R2,R3,R4,R5,R6,R7,R9,R10 | 5,71 | |
| 58 | 2051-24-3 | R1,R2,R3,R4,R5,R6,R7,R8,R9,R10 | 5,44 |
Continuación
Modelado con técnicas de aprendizaje de máquina
Weka 3.8.0 es un software libre que ofrece una amplia gama de técnicas de aprendizaje de máquina para realizar análisis de regresión y clasificación. Las técnicas de regresión que se emplearon en este estudio fueron Gaussian Processes (GP), IBK, Linear Regression (LR), Random Forest (RF) y SMOreg. GP es una técnica de regresión flexible en la que se utilizan procesos aleatorios no paramétricos para la construcción de un modelo clásico [35]. LR es un método en el que se construye un modelo a partir de las multiplicaciones entre las variables y su respectivo coeficiente o “peso” [36]. IBK es una técnica en la que se miden y optimizan distancias para encontrar la instancia del set de entrenamiento más cercana al set de prueba [36]. RF construye un modelo robusto generado a partir de la combinación de árboles de decisión, donde cada árbol depende de los valores de un vector aleatorio [36,37]. El método SMOreg construye un modelo a partir del ajuste de un set de entrenamiento, asignando mayor peso a las instancias que están más cerca al set de prueba [38].
En primer lugar, se realizó una evaluación de atributos con los algoritmos mencionados anteriormente, utilizando cinco como el valor para la validación cruzada [39]. Este proceso se realizó con el objetivo de encontrar el mejor set de descriptores para el modelado, siendo siete el número máximo de variables presentes en el modelo. Se denominó cada set de datos con el prefijo M_i_j donde i es el número del modelo y j es la abreviación de la técnica utilizada. Se utilizó Weka 3.8.0 y MATLAB R2017b para construir los modelos de regresión [33,34].
Validación de los modelos
La validación en cualquier estudio RCEA es de gran importancia ya que se mide la relevancia y la fiabilidad de los modelos matemáticos [40]. Existen dos tipos de validación para modelos RCEA: interna y externa. Una validación interna utiliza los datos que construyen el modelo, mientras que una validación externa utiliza un set de datos aparte [40]. Utilizando el algoritmo k-means de agrupación de datos de Minitab, los compuestos se dividieron en dos conjuntos: el set de entrenamiento (~ 70-75%) y el set de prueba (~ 25-30%), para los procesos de validación externa. Para la primera fase de validación se utilizó Weka 3.8.0 y se analizaron una serie de parámetros estadísticos.
Para la segunda fase se utilizó QSARINS, software que se emplea en la validación y desarrollo de modelos de regresión lineal RCEA [41]. Se analizaron los siguientes parámetros estadísticos para determinar la fiabilidad de los modelos que pasaron la primera fase:
- 1. La colinealidad de las variables se cuantifica con los valores de r de la matriz de correlación, por lo tanto, se esperan valores menores a 0,7 [42].
- 2. El valor del coeficiente de determinación (R2) como una evaluación general de modelo.
- 3. El coeficiente de validación cruzada para la prueba de dejar uno fuera (Q2LOO), el coeficiente de validación cruzada para la prueba de dejar varios fuera (Q2LMO) y el coeficiente de validación externa (Q2ext) como medidores de la predictibilidad del modelo.
- 4. Una prueba de scrambling en la que se cuantifica la aleatoriedad de las predicciones del modelo, por lo tanto, se espera valores bajos en los parámetros R2scr y Q2scr.
RESULTADOS Y DISCUSIÓN
La metodología del presente estudio está resumida en la Figura 2. En total, se construyeron 65 modelos a partir de los descriptores topográficos. Con ayuda de Weka 3.8.0, se obtuvieron 30 modelos utilizando descriptores 3D y 30 modelos utilizando descriptores 2D, para los que cuales se tabuló el coeficiente de correlación (R). Los modelos y su respectivo coeficiente de determinación (R2) están tabulados en las Tablas 2-3 para descriptores 2D y 3D, respectivamente. El R es un parámetro que funciona como indicador de la dependencia lineal entre las variables de un modelo matemático [43]. Utilizando como criterio valores altos para R2, se seleccionaron los 10 mejores modelos con descriptores 2D y los 10 mejores modelos con descriptores 3D para proceder con su validación. Los modelos y su valor de R2 se muestran en las Tablas 4-5. Utilizando MATLAB R2017b, se construyeron 5 modelos de regresión lineal múltiple utilizando un algoritmo genético como método de selección de subconjuntos, y se pasó a la primera fase de validación. Los modelos y sus parámetros estadísticos se muestran en la Tabla 6.
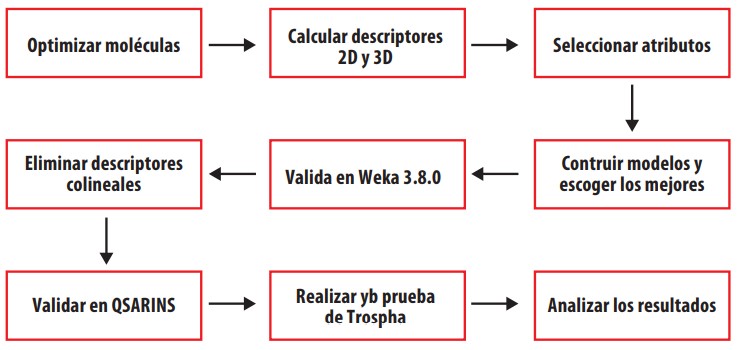
Figura 2
Resumen de la metodología del presente estudio.
| Modelo | Nombre | R2_GP | R2_IBK | R2_LR | R2_RF | R2_SMOR |
| M_1 | IBK_BF_3 | 0.8493 | 0.9349 | 0.8407 | 0.8998 | 0.8405 |
| M_2 | IBK_GS_3 | 0.8493 | 0.8791 | 0.8407 | 0.8998 | 0.8405 |
| M_3 | LR_BF_7 | 0.8851 | 0.8174 | 0.9473 | 0.8316 | 0.9303 |
| M_4 | LR_GS_7 | 0.8851 | 0.8174 | 0.9473 | 0.8316 | 0.9303 |
| M_5 | RF_BF_6 | 0.864 | 0.8066 | 0.8928 | 0.9493 | 0.8748 |
| M_6 | RF_GS_3 | 0.4946 | 0.7813 | 0.8503 | 0.9454 | 0.8429 |
Tabla S1. Modelos construidos con Weka utilizando descriptores 2D
| Modelo | Nombre | R2_GP | R2_IBK | R2_LR | R2_RF | R2 SMOR |
| M_7 | IBK_BF_2 | 0.5721 | 0.9038 | 0.8123 | 0.8501 | 0.8256 |
| M_8 | IBK_GS_2 | 0.5721 | 0.9038 | 0.8123 | 0.8501 | 0.8256 |
| M_9 | LR_BF_5 | 0.7319 | 0.7656 | 0.9103 | 0.8254 | 0.9084 |
| M_10 | LR_GS_5 | 0.7319 | 0.7656 | 0.9103 | 0.8254 | 0.9084 |
| M_11 | RF_BF_7 | 0.6529 | 0.6997 | 0.847 | 0.9111 | 0.7691 |
| M_12 | RF_GS_6 | 0.6726 | 0.8481 | 0.8243 | 0.9139 | 0.7681 |
Tabla S2. Modelos construidos con Weka utilizando descriptores 3D
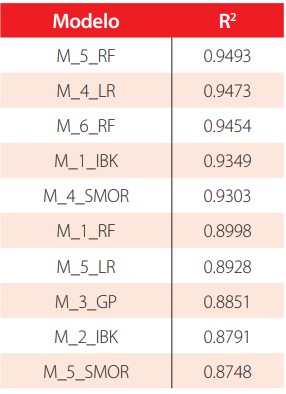
Tabla S3. Coeficiente de correlación para los mejores 10 modelos construidos con Weka utilizando descriptores 2D
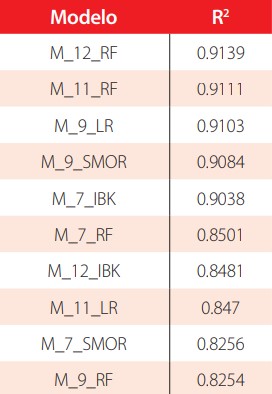
Tabla S4. Coeficiente de correlación para los mejores 10 modelos construidos con Weka utilizando descriptores 3D
| Modelo | R2 |
| M_13 | 0.9346 |
| M_14 | 0.9329 |
| M_15 | 0.918 |
| M_16 | 0.9144 |
| M_17 | 0.9048 |
Tabla S5. Coeficiente de correlación para los modelos construidos con MATLAB
La primera fase de la validación se realizó en Weka 3.8.0 con el propósito de evaluar la linealidad, el error medio absoluto (MAE) y la predictibilidad de cada uno de los modelos construidos. Se entrenó cada modelo con un set de 42 moléculas y se evaluó su predictibilidad con un set de 16 moléculas. Los modelos, sus descriptores y su parámetros estadísticos se encuentran tabulados en la Tabla 7. A partir de los resultados, se escogieron los mejores 3 modelos: M_4_LR, M_13 y M_14. Los modelos seleccionados y sus parámetros estadísticos se muestran en la Tabla 8.
| Set de entrenamiento | Set de prueba | |||||
| Modelo | R | R2 | MAE | R | R2 | MAE |
| M_1_IBK | 0.9303 | 0.8654581 | 0.269 | 0.9652 | 0.931611 | 0.1212 |
| M_1_RF | 0.9266 | 0.8585876 | 0.2523 | 0.9334 | 0.8712356 | 0.2188 |
| M_2_IBK | 0.9303 | 0.8654581 | 0.269 | 0.9652 | 0.931611 | 0.1212 |
| M_3_GP | 0.9098 | 0.827736 | 0.2659 | 0.9562 | 0.9143184 | 0.1883 |
| M_4_LR | 0.9663 | 0.9337357 | 0.1848 | 0.9757 | 0.9519905 | 0.1468 |
| M_4_SMOR | 0.939 | 0.881721 | 0.2339 | 0.9686 | 0.938186 | 0.1691 |
| M_5_LR | 0.8954 | 0.8017412 | 0.2968 | 0.9505 | 0.9034503 | 0.1836 |
| M_5_RF | 0.9379 | 0.8796564 | 0.2602 | 0.9857 | 0.9716045 | 0.1011 |
| M_5_SMOR | 0.8775 | 0.7700063 | 0.3427 | 0.9528 | 0.9078278 | 0.1823 |
| M_6_RF | 0.9262 | 0.8578464 | 0.2853 | 0.9729 | 0.9465344 | 0.1247 |
| M_7_IBK | 0.8893 | 0.7908545 | 0.2882 | 0.9421 | 0.8875524 | 0.2063 |
| M_7_RF | 0.9052 | 0.819387 | 0.3013 | 0.9169 | 0.8407056 | 0.2299 |
| M_7_SMOR | 0.8836 | 0.780749 | 0.3255 | 0.8828 | 0.7793358 | 0.292 |
| M_9_LR | 0.863 | 0.744769 | 0.3416 | 0.9566 | 0.9150836 | 0.1735 |
| M_9_RF | 0.877 | 0.769129 | 0.3026 | 0.9019 | 0.8134236 | 0.2483 |
| M_9_SMOR | 0.8409 | 0.7071128 | 0.3506 | 0.959 | 0.919681 | 0.1909 |
| M_11_LR | 0.7565 | 0.5722923 | 0.3717 | 0.9162 | 0.8394224 | 0.2787 |
| M_11_RF | 0.8448 | 0.713687 | 0.3549 | 0.9707 | 0.9422585 | 0.1584 |
| M_12_IBK | 0.7038 | 0.4953344 | 0.4177 | 0.8302 | 0.689232 | 0.3381 |
| M_12_RF | 0.8842 | 0.7818096 | 0.3165 | 0.9715 | 0.9438123 | 0.1602 |
| M_13 | 0.9552 | 0.912407 | 0.2061 | 0.9456 | 0.8941594 | 0.2149 |
| M_14 | 0.9566 | 0.9150836 | 0.2063 | 0.9268 | 0.8589582 | 0.2624 |
| M_15 | 0.9484 | 0.8994626 | 0.9484 | 0.9434 | 0.8900036 | 0.236 |
| M_16 | 0.9503 | 0.9030701 | 0.2358 | 0.9501 | 0.90269 | 0.2024 |
| M_17 | 0.9446 | 0.8922692 | 0.245 | 0.9428 | 0.8888718 | 0.2073 |
Tabla S6. Parámetros estadísticos de los modelos para la primera fase de validación
Como primer paso de la fase de validación en QSARINS, se optimizaron los modelos con el propósito de eliminar descriptores colineales. Para este análisis, se evaluaron los valores de R de la matriz de correlación. Es de esperarse que estos valores se encuentren entre -0,7 y 0,7 para asegurar que no existe colinealidad entre las variables [42]. La correlación de 0,42 entre los descriptores de M_4_LR se encuentra dentro de este rango. Una vez eliminados los descriptores colineales, se descartó M_14 ya que se construye a partir de los mismos descriptores que M_13. Los resultados del análisis de correlación para los modelos están resumidos en la Figura 3, y la denominación de los descriptores se muestra en las Tablas 9-10. La matriz de correlación para M_13 se encuentra en la Tabla 11.

Descriptores moleculares, parámetros estadísticos y ecuación para M_4_LR.

Descriptores moleculares, parámetros estadísticos y ecuación para M_13.
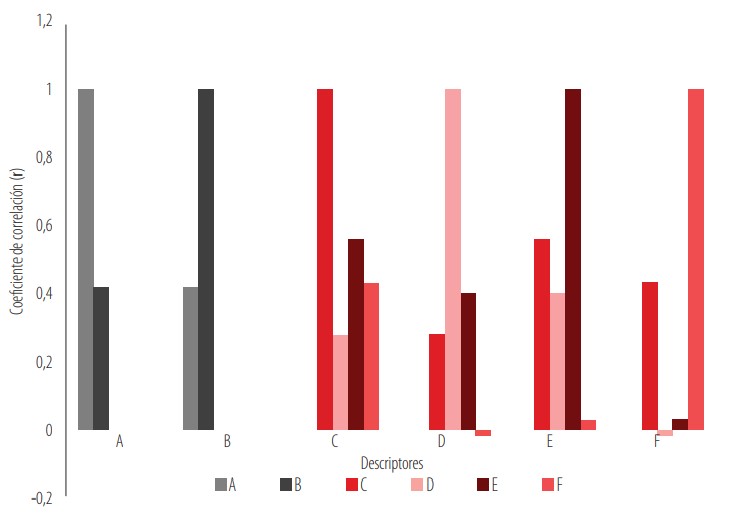
Figura 3
Resultados del análisis de correlación para los descriptores de los modelos de M_4_LR y M_13
Los nombres de los descriptores topográficos corresponden al enfoque matemático que se aplicó sobre las estructuras moleculares 2D y 3D. Las letras minúsculas representan los endone atributos fisicoquímicos que se utilizaron para el cálculo de cada descriptor. Los modelos ingenierías de las Tablas 9-10 están construidos en función de las siguientes propiedades: cargas atómicas (c), masa (m), volumen de Van der Waals (v), electronegatividad (e), índice de refracción (r) y polarizabilidad (p). Las cargas atómicas (c) brindan información de la distribución de densidad electrónica en una molécula[44]. La masa (m) y el volumen de Van der Waals (v) son propiedades estructurales que indican las dimensiones de la molécula [42]. La electronegatividad (e) describe la atendencia de un átomo para atraer electrones hacia sí mismo [45]. El índice de refracción (r) y la polarizabilidad (p) están relacionados con la habilidad de distorsión de la nube electrónica de una especie [42,46]
Por un lado, c, e, m , y v juegan un papel importante en la construcción de M_4_LR. Si bien B tiene un coeficiente más grande, A tiene mayor impacto que B ya que presenta mayor variabilidad. Esto sugiere que la distribución de la carga y el número de sustituyentes clorados influyen en el cálculo del logBCF. Por otro lado, r, p, v, y e juegan un rol importante en la construcción de M_13. F tiene el coeficiente más grande, sin embargo, C cuenta con mayor impacto debido a su variabilidad. F y C son descriptores afectados principalmente por el número de átomos de cloro, debido al aumento de electronegatividad y a una mejor distribución de la carga. De manera general, se puede establecer una relación directa entre el número de átomos de cloro y el logBCFexperimental.
El segundo paso de esta validación es analizar los parámetros estadísticos descritos en la sección de Materiales y Métodos. Valores de R2 cercanos a 1 indican un ajuste óptimo del modelo. Valores altos para Q2LOO, Q2LMO y Q2ext aseguran una buena predictibilidad. Valores bajos para los parámetros de la prueba de scrambling demuestran que el modelo no realiza sus predicciones aleatoriamente. Los descriptores moleculares, parámetros estadísticos y ecuación de los modelos M_4_LR y M_13 se muestran en las Tablas 9-10. Adicionalmente, se realizó una prueba de Tropsha para la validación de dejar uno fuera y para la validación externa. Los resultados de las pruebas para los modelos M_4_LR y M_13 están tabulados en las Tablas 12-13. Finalmente, las Figuras 4-5, muestran una buena correlación lineal entre los valores de logBCF experimentales versus los valores calculados tanto para el conjunto de entrenamiento como de prueba.
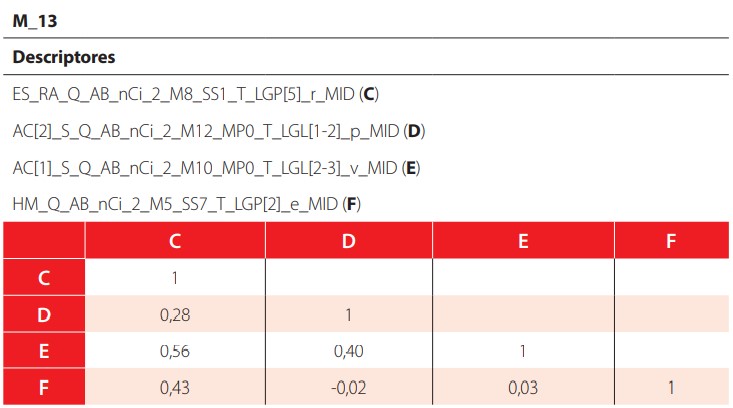
Tabla S7. Matriz de correlación de los descriptores presentes en M_13
| M_4_LR | ||||
| Validación de dejar uno fuera | Validación externa | |||
| Criterio | Resultado | Evaluación | Resultado | Evaluación |
| R2>0,6 | 0,9154 | Pasa | 0,9154 | Pasa |
| R2va >0,5 | 0,8944 | Pasa | 0,9119 | Pasa |
| (R2va - R2vayR2va <0,1 | 0 | Pasa | 0,0005 | Pasa |
| (R2va - R'20)/R2va <0,1 | 0,0056 | Pasa | 0,0145 | Pasa |
| abs(R20-R'20)<0,1 | 0,005 | Pasa | 0,0127 | Pasa |
Criterios de validación de la prueba de Tropsha para M_4_LR.
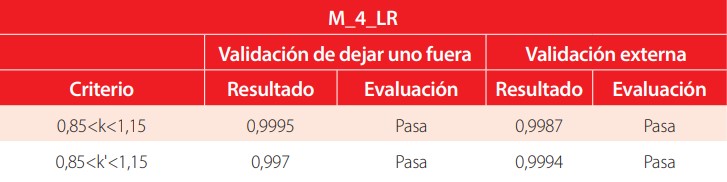
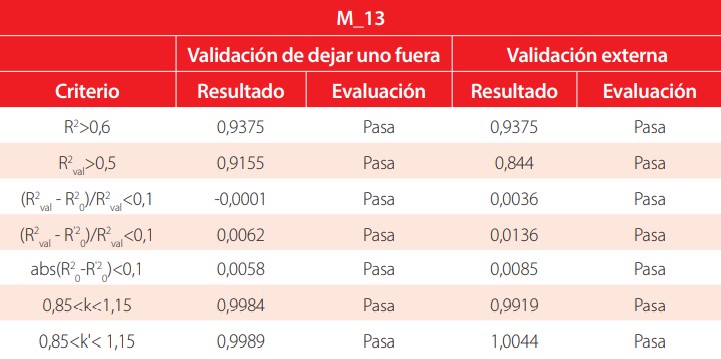
Criterios de validación de la prueba de Tropsha para M_13
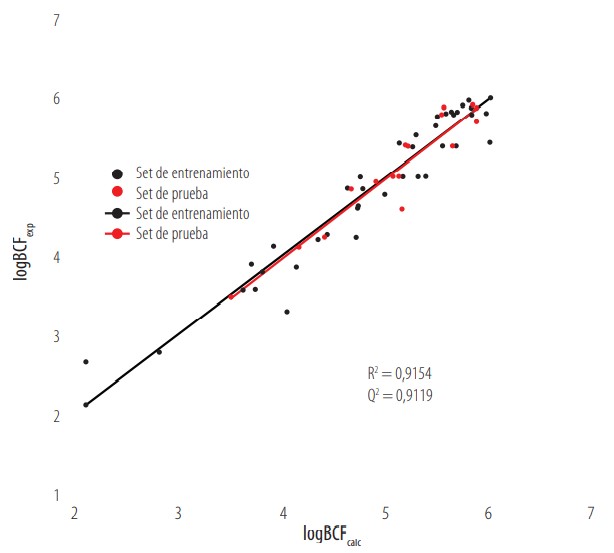
Figura 4
BCF experimental versus BCF calculado con M_4_LR para el set de entrenamiento y el set de prueba
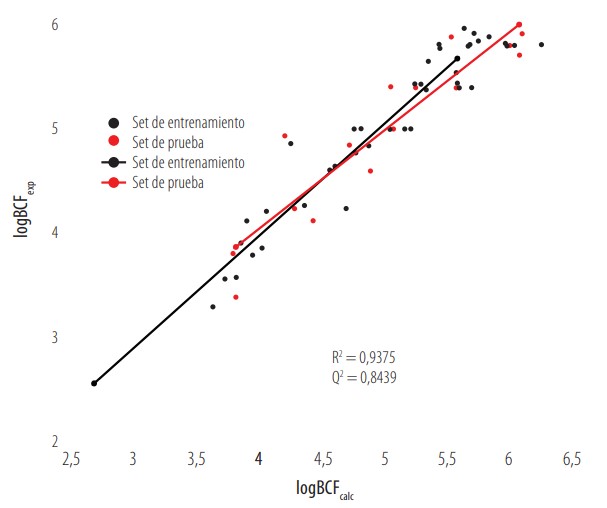
Figura 5
BCF experimental versus BCF calculado con M_13 para el set de entrenamiento y el set de prueba.
CONCLUSIÓN
En el presente estudio, se realizó un modelado RCEA del logBCF de los PCBs utilizando técnicas de aprendizaje de máquina. Dos modelos robustos, construidos a partir de descriptores topológicos, se escogieron según los parámetros estadísticos de las pruebas de validación externa e interna. M_4_LR es un modelo de 2 descriptores con R2= 0,9154, Q2LOO= 0,8944, y Q2ext= 0,9119. M_13 es un modelo de 4 descriptores con R2= 0,9375, Q2LOO= 0,9155, y Q2ext= 0,844. Ambos modelos pasaron todos los criterios de la prueba de Tropsha. Por un lado, M_4_LR destaca por su predictibilidad para la prueba de validación externa. Por otro lado, M_13 presenta una mejor ajuste debido a que su valor de R2 es mayor. Los resultados del estudio son evidencia sólida para demostrar que los descriptores topográficos 2D y 3D, calculados para la estructura optimizada en el nivel de mecánica molecular, son variables muy útiles para la construcción de modelos de regresión que podrían ser usados para predecir el valor de logBCF.
AGRADECIMIENTOS
Agradecemos al programa de Collaboration Grants 2020-2021 de la Universidad San Francisco de Quito por todo el apoyo a esta investigación.
CONTRIBUCIÓN DE LOS AUTORES
Martín Moreno y José Mora concibieron la investigación. José Mora desarrolló la metodología, optimizó las moléculas y calculó los descriptores. Martín Moreno realizó la selección de atributos y construyó los modelos. Martín Moreno y José Mora validaron y optimizaron los modelos, analizaron los resultados, y redactaron el manuscrito.
CONFLICTO DE INTERÉS
Todos los autores declaran no tener ningún conflicto de intereses.
Referencias
Santos, L. L., Miranda, D., Hatje, V., Albergaria-Barbosa, A. C. R., & Leonel, J. (2020). PCBs occurrence in marine bivalves and fish from Todos os Santos Bay, Bahia, Brazil. Marine Pollution Bulletin, 154, 111070. https://doi.org/10.1016/j.marpolbul.2020.111070
Ai, H., Wu, X., Zhang, L., Qi, M., Zhao, Y., Zhao, Q., Zhao, J., & Liu, H. (2019). QSAR modelling study of the bioconcentration factor and toxicity of organic compounds to aquatic organisms using machine learning and ensemble methods. Ecotoxicology and Environmental Safety, 179, 71-78. https://doi.Org/10.1016/j.ecoenv.2019.04.035
Bartalini, A., Muñoz-Arnanz, J., Baini, M., Panti, C., Galli, M., Giani, D., Fossi, M. C., & Jiménez, B. (2020). Relevance of current PCB concentrations in edible fish species from the Mediterranean Sea. Science of The Total Environment, 737, 139520. https://doi.org/10.1016/j.scitotenv.2020.139520
Soni, A. K., Sahu, V. K., & Sahu, S. (2017). DFT-Based Prediction of Bioconcentration Factors of Polychlorinated Biphenyls in Fish Species Using Atomic Descriptors. Asian Journal of Chemistry, 29(11), 2515-2521. https://doi.org/10.14233/ajchem.2017.20839
distribution
Safe, S. H. (1994). Polychlorinated Biphenyls (PCBs): Environmental Impact, Biochemical and Toxic Responses, and Implications for Risk Assessment. Critical Reviews in Toxicology, 24(2), 87-149. https://doi.org/10.3109/10408449409049308
Lunghini, F., Marcou, G., Azam, P., Enrici, M. H., Van Miert, E., & Varnek, A. (2020). Publicly available QSPR models for environmental media persistence. SAR and QSAR in Environmental Research, 31(7), 493-510. https://doi.org/10.1080/1062936X.2020.1776387
Liu, H., Liu, H., Sun, P., &Wang, Z. (2014). QSAR studies of bioconcentration factors of polychlorinated biphenyls (PCBs) using DFT, PCS and CoMFA. Chemosphere, 114, 101-105. https://doi.org/10.1016/j.chemosphere.2014.03.113
Devriese, L. I., De Witte, B., Vethaak, A. D., Hostens, K., & Leslie, H. A. (2017). Bioaccumulation of PCBs from microplastics in Norway lobster (Nephrops norvegicus): An experimental study. Chemosphere, 186, 10-16. https://doi.org/10.1016/j.chemosphere.2017.07.121
Yeo, B. G., Takada, H., Yamashita, R., Okazaki, Y., Uchida, K., Tokai, T., Tanaka, K., & Trenholm, N. (2020). PCBs and PBDEs in microplastic particles and zooplankton in open water in the Pacific Ocean and around the coast of Japan. Marine Pollution Bulletin, 151, 110806. https://doi.org/10.1016/j.marpolbul.2019.110806
Soni, A. K., Singh, P., & Sahu, V. K. (2020). DFT-Based Prediction of Bioconcentration Factors of Polychlorinated Biphenyls in Fish Species Using Molecular Descriptors. Advances in Biological Chemistry, 10(01), 1-15. https://doi.org/10.4236/abc.2020.101001
Mikolajczyk, S., Warenik-Bany, M., Maszewski, S., & Pajurek, M. (2020). Dioxins and PCBs - Environment impact on freshwater fish contamination and risk to consumers. Environmental Pollution, 263, 114611. https://doi.org/10.1016/j.envpol.2020.114611
Gad, S. C. (2005). Toxicity Testing, Aquatic. En P. Wexler (Ed.), Encyclopedia of Toxicology (Second Edition) (pp. 233239). Elsevier. https://doi.org/10.1016/B0-12-369400-0/00963-7
Schmitz, K. S. (2018). Chapter 4—Life Science. En K. S. Schmitz (Ed.), Physical Chemistry (pp. 755-832). Elsevier. https://doi.org/10.1016/B978-0-12-800513-2.00004-8
Peake, B. M., Braund, R., Tong, A. Y. C., & Tremblay, L. A. (2016). 5—Impact of pharmaceuticals on the environment. En B. M. Peake, R. Braund, A. Y. C. Tong, & L. A. Tremblay (Eds.), The Life-Cycle of Pharmaceuticals in the Environment (pp. 109-152). Woodhead Publishing. https://doi.org/10.1016/B978-1-907568-25-1.00005-0
Lunghini, F., Marcou, G., Azam, P., Patoux, R., Enrici, M. H., Bonachera, F., Horvath, D., & Varnek, A. (2019). QSPR models for bioconcentration factor (BCF): Are they able to predict data of industrial interest? SAR and QSAR in Environmental Research, 30(7), 507-524. https://doi.org/10.1080/1062936X.2019.1626278
Marigómez, I. (2014). Environmental Risk Assessment, Marine. En P. Wexler (Ed.), Encyclopedia of Toxicology (Third Edition) (pp. 398-401). Academic Press. https://doi.org/10.1016/B978-0-12-386454-3.00556-X
Silakari, O., & Singh, P. K. (2021). Chapter 2 - QSAR: Descriptor calculations, model generation, validation and their application. En O. Silakari & P. K. Singh (Eds.), Concepts and Experimental Protocols of Modelling and Informatics in Drug Design (pp. 29-63). Academic Press. https://doi.org/10.1016/B978-0-12-820546-4.00002-7
Muratov, E. N., Bajorath, J., Sheridan, R. P., Tetko, I. V., Filimonov, D., Poroikov, V., Oprea, T. I., Baskin, I. I., Varnek, A., Roitberg, A., Isayev, O., Curtalolo, S., Fourches, D., Cohen, Y., Aspuru-Guzik, A., Winkler, D. A., Agrafiotis, D., Cherkasov, A., & Tropsha, A. (2020). QSAR without borders. Chemical Society Reviews, 49(11), 3525-3564. https://doi.org/10.1039/D0CS00098A
Chandrasekaran, B., Abed, S. N., Al-Attraqchi, O., Kuche, K., & Tekade, R. K. (2018). Chapter 21—Computer-Aided Prediction of Pharmacokinetic (ADMET) Properties. En R. K. Tekade (Ed.), Dosage Form Design Parameters (pp. 731-755). Academic Press. https://doi.org/10.1016/B978-0-12-814421-3.00021-X
Gund, T. (1996). 3—Molecular Modeling of Small Molecules. En N. C. Cohen (Ed.), Guidebook on Molecular Modeling in Drug Design (pp. 55-92). Academic Press. https://doi.org/10.1016/B978-012178245-0/50004-4
Errol G. Lewars. (2011). Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics (2a ed.). Springer Netherlands.
Tosco, P., Stiefl, N., & Landrum, G. (2014). Bringing the MMFF force field to the RDKit: Implementation and validation. Journal of Cheminformatics, 6(1), 37. https://doi.org/10.1186/s13321-014-0037-3
García-Jacas, C. R., Marrero-Ponce, Y., Acevedo-Martínez, L., Barigye, S. J., Valdés-Martiní, J. R., & Contreras-Torres, E. (2014). QuBiLS-MIDAS: A parallel free-software for molecular descriptors computation based on multilinear algebraic maps. Journal of Computational Chemistry, 35(18), 1395-1409. https://doi.org/10.1002/jcc.23640
Echols, K. R., Gale, R. W., Schwartz, T. R., Huckins, J. N., Williams, L. L., Meadows, J. C., Morse, D., Petty, J. D., Orazio, C. E., & Tillitt, D. E. (2000). Comparing Polychlorinated Biphenyl Concentrations and Patterns in the Saginaw River Using Sediment, Caged Fish, and Semipermeable Membrane Devices. Environmental Science & Technology, 34(19), 4095-4102. https://doi.org/10.1021/es001169f
Geyer, H. J., Scheunert, I., Brüggemann, R., Steinberg, C., Korte, F., & Kettrup, A. (1991). QSAR for organic chemical bioconcentration in Daphnia, algae, and mussels. Science of The Total Environment, 109-110, 387-394. https://doi.org/10.1016/0048-9697(91)90193-I
Devillers, J., Bintein, S., & Domine, D. (1996). Comparison of BCF models based on log P. Chemosphere, 33(6), 10471065. https://doi.org/10.1016/0045-6535(96)00246-9
Wei, D., Zhang, A., Wu, C., Han, S., & Wang, L. (2001). Progressive study and robustness test of QSAR model based on quantum chemical parameters for predicting BCF of selected polychlorinated organic compounds (PCOCs). Chemosphere, 44(6), 1421-1428. https://doi.org/10.1016/S0045-6535(00)00538-5
Sa^an, M. T., Erdem, S. S., Özpinar, G. A., & Balcioglu, I. A. (2004). QSPR Study on the Bioconcentration Factors of Nonionic Organic Compounds in Fish by Characteristic Root Index and Semiempirical Molecular Descriptors. Journal of Chemical Information and Computer Sciences, 44(3), 985-992. https://doi.org/10.1021/ci0342167
Lu, X., Tao, S., Cao, J., & Dawson, R. W. (1999). Prediction of fish bioconcentration factors of nonpolar organic pollutants based on molecular connectivity indices. Chemosphere, 39(6), 987-999. https://doi.org/10.1016/S0045-6535(99)00020-X
Lu, X., Tao, S., Hu, H., & Dawson, R. W. (2000). Estimation of bioconcentration factors of nonionic organic compounds in fish by molecular connectivity indices and polarity correction factors. Chemosphere, 41(10), 1675-1688. https://doi.org/10.1016/S0045-6535(00)00050-3
Fox, K., Zauke, G. P., & Butte, W. (1994). Kinetics of Bioconcentration and Clearance of 28 Polychlorinated Biphenyl Congeners in Zebrafish (Brachydanio rerio). Ecotoxicology and Environmental Safety, 28(1), 99-109. https://doi.org/10.1006/eesa.1994.1038
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann, P., & Witten, I. H. (2009). The WEKA data mining software: An update. ACM SIGKDD Explorations Newsletter, 11(1), 10-18. https://doi.org/10.1145/1656274.1656278
Thirumalai, K., Singh, A., & Ramesh, R. (2011). A MATLABTM code to perform weighted linear regression with (correlated or uncorrelated) errors in bivariate data. Journal of the Geological Society of India, 77(4), 377-380. https://doi.org/10.1007/s12594-011-0044-1
Seeger, M. (2004). Gaussian processes for machine learning. International Journal of Neural Systems, 14(02), 69106. https://doi.org/10.1142/S0129065704001899
Cabrera, N., Mora, J. R., & Marquez, E. A. (2019). Computational Molecular Modeling of Pin1 Inhibition Activity of Quinazoline, Benzophenone, and Pyrimidine Derivatives. Journal of Chemistry, 2019, 1-11. https://doi.org/10.1155/2019/2954250
Breiman, L. (2001). Random Forests. Machine Learning, 45(1), 5-32. https://doi.org/10.1023/A:1010933404324
Li, C., & Jiang, L. (2006). Using Locally Weighted Learning to Improve SMOreg for Regression. En Q. Yang & G. Webb (Eds.), PRICAI 2006: Trends in Artificial Intelligence (pp. 375-384). Springer. https://doi.org/10.1007/978-3-540-36668-3_41
Bugeac, C. A., Ancuceanu, R., & Dinu, M. (2021). QSAR Models for Active Substances against Pseudomonas aeruginosa Using Disk-Diffusion Test Data. Molecules, 26(6), 1734. https://doi.org/10.3390/molecules26061734
Veerasamy, R., Rajak, H., Jain, A., Sivadasan, S., Varghese, C. P., & Agrawal, R. K. (2011). Validation of QSAR Models—Strategies and Importance. International Journal of Drug Design and Discovery, 2(3), 511-519.
Gramatica, P., Chirico, N., Papa, E., Cassani, S., & Kovarich, S. (2013). QSARINS: A new software for the development, analysis, and validation of QSAR MLR models. Journal of Computational Chemistry, 34(24), 2121-2132. https://doi.org/10.1002/jcc.23361
Cabrera, N., Mora, J. R., Márquez, E., Flores-Morales, V., Calle, L., & Cortés, E. (2021). QSAR and molecular docking modelling of anti-leishmanial activities of organic selenium and tellurium compounds. SAR and QSAR in Environmental Research, 32(1), 29-50. https://doi.org/10.1080/1062936X.2020.1848914
Montgomery, D. C., & Runger, G. C. (2014). Applied Statistics and Probability for Engineers (6a ed.). John Wiley & Sons.
Mao, J. X. (2014). Atomic Charges in Molecules: A Classical Concept in Modern Computational Chemistry. Journal of Postdoctoral Research, 2(2), 4. https://doi.org/10.14304/SURYA.JPR.V2N2.2
Gupta, V. P. (2016). 12—Characterization of Chemical Reactions. En V. P. Gupta (Ed.), Principles and Applications of Quantum Chemistry (pp. 385-433). Academic Press. https://doi.org/10.1016/B978-0-12-803478-1.00012-1
House, J. E. (2013). Chapter 9—Acid-Base Chemistry. En J. E. House (Ed.), Inorganic Chemistry (Second Edition) (pp. 273-312). Academic Press. https://doi.org/10.1016/B978-0-12-385110-9.00009-1