



MHPM Solution to MHD Fluid Flow Through Porous Medium with an Exponentially Variable Permeability
Flujo de fluido MHD en medio poroso de permeabilidad exponencial resuelto mediante el método modificado de perturbación homotópica
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
Received: 01 May 2021
Accepted: 07 July 2021
Resumen: En este artículo se estudia y analiza el flujo completamente desarrollado de un fluido magneto-reológico a través de un medio poroso no isotrópico bajo el efecto de un campo magnético externo, uniforme y transversal. La permeabilidad se toma como una función de distribución exponencial de la dirección transversal. Para esto se ha utilizado la ecuación de Darcy-Brinkman-Lapwood-Lorentz para el flujo de fluidos en medios porosos y se ha resuelto en condiciones de límite antideslizantes mediante el método modificado de perturbación homotópica y los resultados fueron validados por el método numérico del disparo. El análisis de los resultados se ha realizado a través de las variables: velocidad, flujo volumétrico y esfuerzo de deformación en la pared. Estos demuestran que los parámetros más importantes son el número de Darcy y la relación de viscosidad. Asimismo, se demuestra que valores bajos de estos parámetros minimizan los efectos de cizallamiento viscoso de Brinkman.
Palabras clave: Régimen de Brinkman, Número magnético de Hartmann, permeabilidad exponencial, fluido magneto-reológico.
Abstract: In this work, we study and analyze the fully developed flow of a magnetorheological fluid through an inhomogeneous porous medium of variable permeability under the influence of an external, uniform, and transversal magnetic field. Permeability is modelled as an exponential distribution function of the transverse direction. The Darcy-Lapwood- Brinkman-Lorentz equation, which governs this type of fluid flow in porous media, is solved under the no-slip boundary conditions by the Modified Homotopy Perturbation Method. Solutions, and results, are validated using the Numerical Shooting Method. Results are analyzed to better understand the influence of fluid and flow parameters on the velocity, volumetric flow rate, and wall shear stress. Analysis in this work shows that the two most important parameters are the Darcy number and the viscosity ratio. Low values of these parameters undermine Brinkman’s viscous shear effects.
Keywords: Brinkman regime, Hartmann magnetic number, exponential permeability, magnetorheological fluid.
INTRODUCTION
Single- and multi-phase fluid flow through and over porous layers are encountered in the natural environment and have a host of practical applications in industry. In natural environments, groundwater flow, flow in channels and rivers over porous beds, flow of oil and gas in reservoirs, deep-bed filtration processes, the movement of nutrients into plants, and the flow of blood in human tissues are only a few examples of flow through naturally occurring porous layers. In industry, heat and mass transfer in porous layers continues to receive considerable attention due to its various applications, which span many aspects of human endeavor. These include applications in lubrication theory in mechanisms with porous lining, design of industrial filters and liquid-dust separators, design of heat exchangers, and membrane analysis. These, and many other applications, have been extensively reviewed by various authors (cf. Nield and Bejan, [1], Rudraiah, [2], and the references therein).
A special type of flow that is of particular interest to the current work is the magnetohydrodynamic (MHD) flow through variable permeability porous media. This flow has many industrial applications in fields that include power generation, oil industry, refining of crude oil, and polymer technology. Magnetohydrodynamic pumps and accelerators, aerodynamic heating, electrostatic precipitation, aerosols and sprays, biotechnology, medicine, optical modulators, tunable optical fiber filters, optical grating, optical switches, stretching of plastic sheets, and metallurgy are further areas of applications that underscore the importance of MHD flow in industrial settings. Further details on these and many other applications can be found in the works of Kuzhir et al. [3], Attia and Abdeen [4], Barcena et al. [5], Mishra et al. [6], and Shehzad and Hayat [7].
The above and many other applications have given impetus to the explosive knowledge witnessed over the past eight decades in the area of porous media studies. Recent years, however, witnessed an escalation of interest in the study of fluid flow through porous media with variable porosity and permeability. This interest stems from two broad reasons, the first of which is that naturally occurring porous media does not possess constant porosity and permeability. The second is that accurate and realistic modelling of flow through porous media must take into account the porous microstructure of the flow domain, which influences the effective viscosity of the fluid in the porous medium and inevitably leads to the need for flow models with variable porosity and permeability [8]. Take, for example, the celebrated Brinkman’s equation [9], which is the most recognized model of fluid flow through porous media in the presence of macroscopic boundary (cf. Hamdan & Kamel [10] and the references therein), due to its incorporation of a viscous shear term necessary to handle no-slip condition on a macroscopic, solid boundary.
Various authors have discussed validity and limitations of Brinkman’s equation (cf. Auriault [11], Nield and Bejan [1], and the references therein). Rudraiah [2], suggested that Brinkman’s equation is the most appropriate model of flow through porous layers of finite depth, while Parvazinia et. al. [12] determined that when Brinkman’s equation is used (depending on Darcy number, Da), three different flow regimes are obtained: a free flow regime (Da ≥ 1), a Brinkman regime ( 10-6 ≤ Da < 1), and a Darcy regime (Da < 10-6). Nield [13] elegantly concluded that the use of Brinkman’s viscous shear term requires a redefinition of the porosity near a solid boundary due to a process referred to as channeling. The above investigations underscore the need for variable permeability flow modelling in realistic applications of flow through porous media in the presence of solid boundaries. Sahraoui and Kaviany [14] and Kaviany [15] studied the case of flow through variable permeability media when using Brinkman’s equation and emphasized the need for variable permeability near macroscopic boundaries, whether slip or no-slip conditions are applied. Lundgren [16] showed that the effective viscosity depends on the porosity of the medium and the viscosity of the base fluid, and formally proved the validity of the Brinkman equation for dilute concentration of particles.
Although permeability is a tensorial quantity in three-dimensional flow through naturally occurring and heterogeneous media, idealizations of flow through two space dimensions and unidirectional flow through porous layers have given rise to variable permeability modelling using algebraic functions of one of the space variables. A number of variable permeability models are available in the literature and serve a spectrum of flow situations and flow domains of specific industrial applications (cf. Cheng [17], Hamdan and Abu Zaytoon [18], Hamdan and Kamel [10], and the references therein). An important subset of the available variable permeability models that received the most attention in the literature is summarized in what follows.
Elaiw et al. [19], Hassanien [20], Hassanien et al. [21], and Jang and Chen [22] reduced the two-dimensional permeability model of Chandrasekhara et al. [23] to a one-dimensional model of the form: K(y)=K∞ (1 + de-y/γ), where d and y are constants, K(y) is the permeability function and K∞ is the value of permeability at the edge of the boundary layer. Other authors employed the two-dimension permeability model of Chandrasekhara et al. (cf. Chandrasekhara et al. [24] [25] [23] Goldstein et al. [26]). Other important models of one-dimensional permeability variation used in soil mechanics include those found in Schiffman and Gibson [27] and Mahmoud and Deresiewicz [28]. Cheng [17] used the model K(y)=Ko (1 + βy* )η, where β and η are parameters of curve fittings, d is a characteristic length of geometry, Ko is the characteristic permeability of the medium, and y* = y/d. The value normally used in the literature for η is 2.
Rees and Pop [29] studied the free convection in a vertical porous medium with the exponential model of permeability K = K∞ + (Kw - K∞)e-y/d, where is the permeability at the wall, is the permeability of the ambient medium, and d is the length scale over which the permeability varies. Additionally, they indicated when a porous medium is bounded by an impermeable surface, it is well known that the porosity and hence the permeability increase near that surface. Alloui et al. [30] investigated the natural convection in a porous layer with an exponentially variable permeability as a function of the thickness of the layer, of the form K = K0ecy where c is a fitting parameter and K0 is an average permeability. Abu Zaytoon [24] analyzed the behavior of flow in a porous layer with exponential permeability variations using the permeability function K(y) = 1/2e (e – e-y). Choukairy and Bennacer [31] presented a numerical and analytical analysis of the thermo-solutal convection in a heterogeneous porous layer enclosed in a rectangular cavity with the permeability changing with depth, using the model K(y) = 1 + 4 (2y)n where n is a parameter.
A problem of interest, and the subject matter of this work, is the MHD flow between two parallel plates, known as Hartmann flow (cf. Hartmann and Lazarus [32], Jeffrey [33], Müller and Bühler [34], Rothmayer [35], and the references therein). In the absence of MHD effects, fluid flow through a porous channel bounded by two flat plates has received considerable attention in the literature due to the importance of this configuration in furthering our understanding of flow behaviour through porous channels (cf. Awartani and Hamdan [36], Fu et al. [37], Harwin [38], Kaviany [39], Liu et al. [40], and the references therein).
When magnetorheological effects are taken into account, Pillai et al. [41] offered a study of the steady flow of a magnetorheological fluid in an inclined channel over a porous bed with a decaying exponential permeability that depends on the depth of the porous bed, using the model K(y) = K0e-cy, proposed by Sinha and Chadda [42]. Narasimha Murthy and Feyen [43] studied the influence of the variable permeability on the two MHD basic flows in porous media, using the variable permeability model K(y) = K0(1 + y/h )2, where K0 is the permeability in the interior of the porous medium and h the porous layer thickness. Two other important variable permeability models in the study of MHD flow have been reported in the works of Mathew [44] and Srivastava and Deo [45]. Mathew [44] employed a periodic variable permeability model in the study of two-dimensional MHD convective heat transfer through a vertical porous channel using the permeability model K(y) = K0(1 + εcos (πy))-1, while Srivastava and Deo [45] employed the variable permeability model K = K0(1 - εy)2, where 0 ≤ ε < 1, in their study of Couette and Poiseuille MHD plane flow in a porous channel.
The model of variable permeability employed by Alloui et al. [30], namely, K(y) = K0ecy, is of interest in this current work, in which we investigate the fully developed MHD flow through a porous medium bounded by parallel plates. Interest in this model stems from the fact that permeability is exponentially increasing and places higher permeability in one of the regions of the infinite channel. The objective here is to provide insight into the effects of the flow and medium parameters (Darcy number, Hartmann number, and viscosity ratio) on the flow characteristics of velocity, flow rate, and wall shear stress. Furthermore, since a choice of variable permeability model influences our understanding of the intrinsic features of the flow, data obtained in this work is intended to provide a baseline and a benchmark for the sake of comparison when other variable permeability models are employed.
In using the model of Alloui et al. [30], this work provides a formulation of the MHD flow problem through a porous channel of infinite extent between two parallel, horizontal, and impermeable plates, and provides its solution by using the Modified Homotopy Perturbation Method (MHPM) of He [46]. The solution obtained using the currently proposed method is compared with the numerical solution of the same problem using the Numerical Shooting Algorithm, in order to validate the results obtained.
Numerical calculations were performed using Mathematica® V 12.3 symbolic software.
MATHEMATICAL FORMULATION OF THE PROBLEM
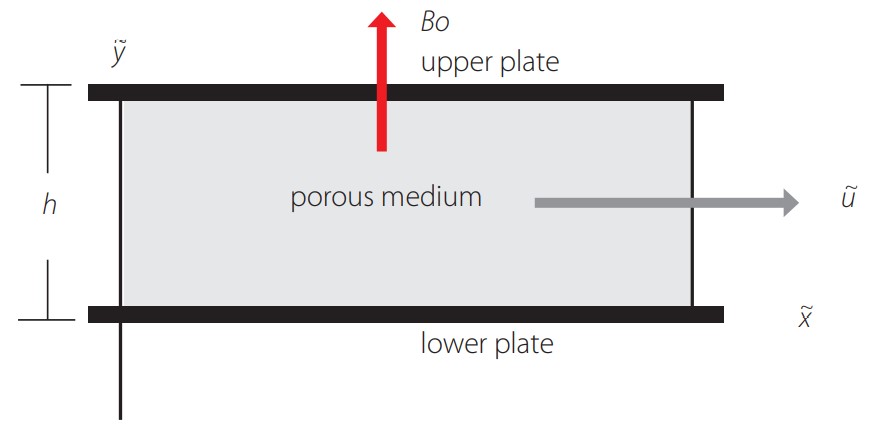
Sketch of the porous medium. The flow direction is the direction.
Consider the fully developed flow through the infinite porous channel depicted in Fig. 1, of a magnetorheological, incompressible, and electrically conducting fluid. The external magnetic field is transverse and uniform, without induced magnetic field inside the porous medium because of a very low Reynolds magnetic number. The electric field in the porous medium is very small or negligible. The pressure gradient is constant and drives the flow along the longitudinal axis. The permeability model of the porous medium is assumed to depend on the transverse direction and takes the following form:
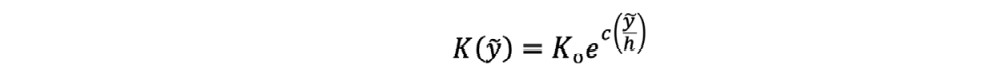 (1)
(1)where c is a positive number and K0 is the average permeability of the medium.
GOVERNING EQUATIONS
Geindreau and Auriault [47] provided comprehensive analysis of MHD flow through porous media, which includes development of the full set of equations governing the flow. The momentum equation used in their analysis is the one obtained by Rudraiah et.al. [48] through modification of Brinkman’s equation and Darcy’s law. This equation is used in the current work (in the form listed as equation (3), below).
The governing equations for the fluid flow in the porous medium are the following continuity and momentum equations, respectively:
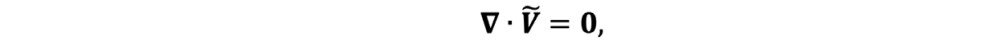 (2)
(2)
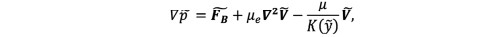 (3)
(3)where , is the Lorentz body-force, which is:
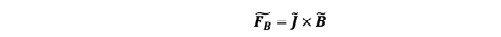 (4)
(4)and, the current density, is defined as:
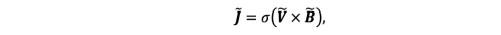 (5)
(5)where is the dimensional velocity field, in which is assumed that. Additionally, K = () is the dimensional permeability, the magnetic field intensity, a the electrical conductivity of the fluid,the pressure gradient, the fluid viscosity, and the effective viscosity in the porous medium.
For fully developed flow along the x-axis, Eqs. (1) to (5) reduce to:
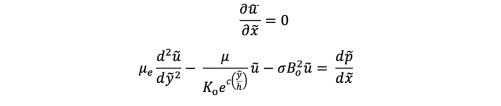 (6) and (7)
(6) and (7)Equation (8) implies that. The no-slip boundary conditions for Eq. (7), are thus given by:
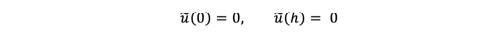 (8)
(8)To convert Eq. (7) into a non-dimensional form, the following variables are used:
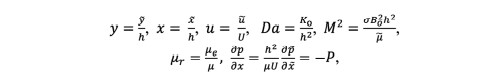 (9)
(9)where U is the characteristic velocity, M the Hartmann number, Da the Darcy number, the viscosity ratio, and P (P > 0) the non-dimensional pressure gradient.
Using (9), Eq. (7) takes the following dimensionless form:
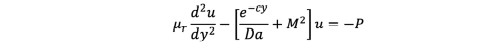 (10)
(10)Dimensionless boundary conditions, Eq. (10), take the form:
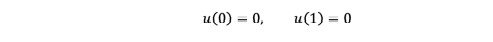 (11)
(11)The physical quantities to investigate in this work are the dimensionless volumetric flow rate, and the dimensionless shear stress , defined, respectively, as:
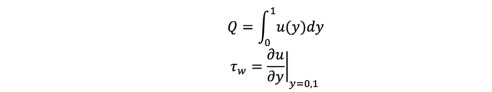 (12) and (13)
(12) and (13)where the subscripts 0 and 1 in Eq. (13) indicate the shear stress at the lower and upper walls, respectively.
If we try to solve Eq. (10) analytically by using the transformation z = e-cy, we obtain the following differential equation:
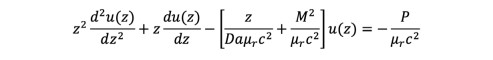 (14)
(14)Equation (14) is a hyperbolic Bessel differential equation, which has the analytical solution:
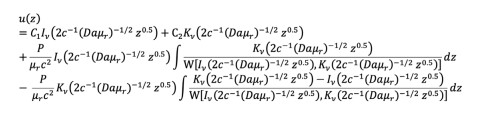 (15)
(15)where
C1 and C2 are constants to be evaluated at boundary conditions, Iv and Kv are the modified Bessel functions of the first and second kind,
respectively, W is the Wronskian of , and is the order of the modified Bessel functions, which is
equal to:
, and is the order of the modified Bessel functions, which is
equal to:
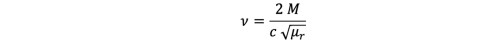 (16)
(16)Therefore, the analytical solution of u(y) can be written as:
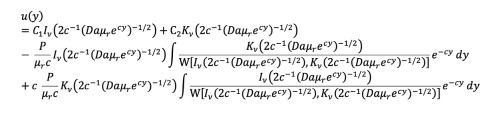 (17)
(17)This result demonstrates the validity of the statement made by Merabet et al. [49] as they indicated that for the case of flow through porous media, as governed by the Darcy-Lapwood-Brinkman model, exact solutions are rare. It was reported that in some cases, it is possible to find exact solutions, but this requires special functions, such as the Airy’s, Bessel or modified Bessel, or Nield-Kuznetsov functions (cf. Cheng [17], Abu Zaytoon et al. [50], Alzahrani et al. [3], and the references therein).
Equation (17) is hardly tractable, even though it possesses an analytical solution. Therefore, we seek to find a solution that can produce some results in order to provide some insight into the flow regime. To accomplish this, we base the current work on the work of Seyf and Rassoulinejad-Mousavi [51] who used the Homotopy Perturbation Method (HPM) technique to solve fluid flow and heat transfer problems in saturated porous media. However, the HPM technique is implemented here in a modified version introduced by He [46]. Using this modified version, we obtain an approximate solution of Eq. (10).
As a means of validating this modified version and the results obtained, we offer a comparison of the results with those that we obtain using a Numerical Shooting Method (NSM).
Analysis of Homotopy Perturbation Method (HPM)
To illustrate the basic concept of Homotopy Perturbation Method (cf. He [52] [53] [54] [55] [56] [57] Jazbi and Moini [58], Usman et al. [59], and the references therein), we consider the following nonlinear functional equation:
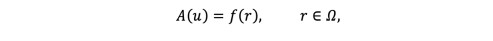 (18)
(18)with the boundary conditions
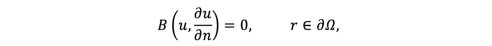 (19)
(19)where A is a general functional operator, B the boundary operator, f(r) the known analytic function, and the boundary of the domain .
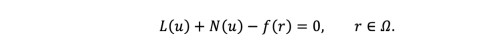 (20)
(20)The operator A is decomposed into the sum of a linear and a nonlinear part, as A(u) = L(u) + N(u), where L is the linear and N is the nonlinear part. Eq. (18) can thus be written as:
We construct a Homotopy v(r, p): Ω x [0, 1] → R satisfying:
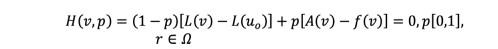 (21)
(21)Hence
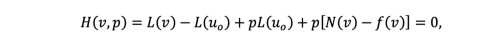 (22)
(22)where is an initial approximation for the solution of Eq. (20) that satisfies the boundary conditions, as:
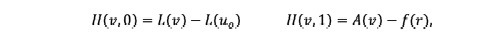 (23)
(23)where p ∊ [0, 1] is the embedding parameter. This shows that H(v, p) continuously traces an implicitly defined curve from a starting point H(, 0) to a solution H(v, 1). The embedding parameter p increases monotonously from zero to one as the trivial linear part L(u) = 0 deforms continuously to the original problem A(u) = (r). The embedding parameter p can be considered as an expanding parameter to obtain
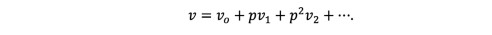 (24)
(24)The solution is obtained by taking the limit as p tends to 1 in Eq. (24), namely
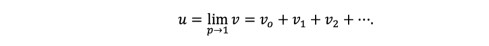 (25)
(25)He’s Modified Homotopy Perturbation Method (MHPM)
The method proposed by He [46] consists of the use of an initial approximation (or a trial function) of the form:
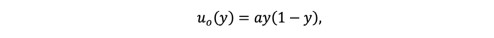 (26)
(26)where is an unknown constant to be determined, and the trial function satisfies the boundary conditions. According to the initial approximation, a homotopy should be constructed such that:
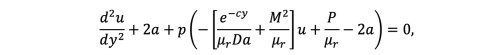 (27)
(27)and, when p = 0, the solution of Eq. (27) is Eq. (26). When p = 1, we recover solution (25).
The solution procedure is similar to that of classical perturbation method. Using p as an expanding parameter, as one would in classic perturbation method, we obtain:
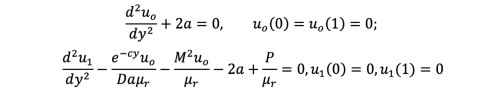 (28)
(28)The optimal identification of the unknown parameter in the trial function is a method of weighted residuals, namely, the least squares method:
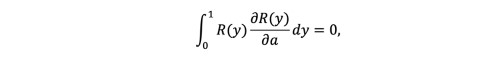 (29)
(29)where R is the residual given by R(u(y)) = L(u) + N(u).
Setting p = 1, we obtain the first-order approximate solution which reads:
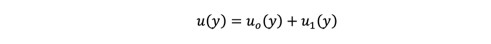 (30)
(30)Numerical Shooting Method
In order to provide validation for the results obtained using the Modified Homotopy ingemenas Perturbation Method (MHPM), we provide a solution for obtained using the Numerical Shooting Method (NSM). Computations have been carried out using Mathematica® V 12.3 symbolic software. Comparisons are discussed in the section of Results and Analysis, using data in Tables 1 and 2.
| M = 1, Da = 1, c = 0.35, P = 5, µr = 1 | |||
| y | MHMP | NSM | Difference |
| 0 | 0 | 0 | 0 |
| 0.1 | 0.19279852281653900 | 0.19275803841960400 | 4.04843969349922E-05 |
| 0.2 | 0.33924641849525300 | 0.33921985612208700 | 2.65623731660058E-05 |
| 0.3 | 0.44213497291476800 | 0.44216027115848900 | 2.52982437209948E-05 |
| 0.4 | 0.50336190350106800 | 0.50343333593362400 | 7.14324325560289E-05 |
| 0.5 | 0.52397533124740600 | 0.52405245422526400 | 7.71229778580018E-05 |
| 0.6 | 0.50421483755058900 | 0.50424983725450200 | 3.49997039129635E-05 |
| 0.7 | 0.44354976981598500 | 0.44351768841736000 | 3.20813986249835E-05 |
| 0.8 | 0.34071495142945700 | 0.34063365481816200 | 8.12966112950231E-05 |
| 0.9 | 0.19374394372467200 | 0.19367172438820800 | 7.22193364639800E-05 |
| 1 | -0.00000000000006858 | 0.00000000159566237 | 1.59573095046188E-09 |
Comparison of u(y) obtained by MHPM and NSM
| M =1, Da = 0.1, c = 0.35, P = 5, µr = 8 | |||
| y | MHMP | NSM | Difference |
| 0 | 0 | 0 | 0 |
| 0.1 | 0.02535938910102333 | 0.02535795330998652 | 1.43579103679958E-06 |
| 0.2 | 0.04479575192615648 | 0.04479557849314981 | 1.73433006601942E-07 |
| 0.3 | 0.05855152602734696 | 0.05855410186180611 | 2.57583445920084E-06 |
| 0.4 | 0.06678397121908308 | 0.06678838725043413 | 4.41603135109547E-06 |
| 0.5 | 0.06957245254763313 | 0.06957617226896888 | 3.71972133569876E-06 |
| 0.6 | 0.06692524042597543 | 0.06692575550897644 | 5.15083001001448E-07 |
| 0.7 | 0.05878585508979328 | 0.0587822835297458 | 3.57156004739817E-06 |
Comparison of u(y) obtained by MHPM and NSM
| M =1, Da = 0.1, c = 0.35, P = 5, µr = 8 | |||
| y | MHMP | NSM | Difference |
| 0.8 | 0.0450389811453929 | 0.04503294332770041 | 6.03781769249745E-06 |
| 0.9 | 0.02551597666129448 | 0.025511144614260108 | 4.83204703429982E-06 |
| 1 | 6.123231297622667E-15 | -9.6930110788705E-10 | 9.69307231118348E-10 |
RESULTS AND ANALYSIS
Solutions obtained by MHPM from Eqs. (26)-(30) are as follows:
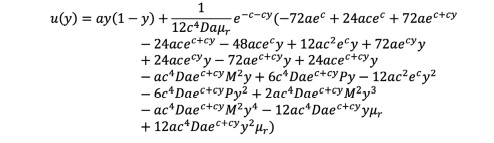 (31)
(31)with parameter a given by:
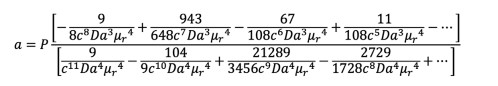 (32)
(32)The dimensionless volumetric flow rate and the shear stress are given, respectively, by:
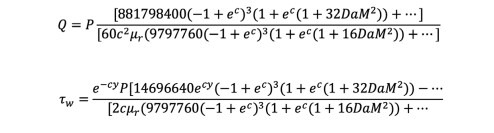 (33) and (34)
(33) and (34)In Tables 1 and 2 we provide validation of MHPM by comparing values of velocity obtained using MHPM with those obtained using NSM, for some chosen values of the parameters M, Da, c, P and ur Both Tables illustrate excellent agreement for all parameters tested, with computed values in agreement for at least six significant digits. Maximum absolute error in both Tables is less than 5x10-5.
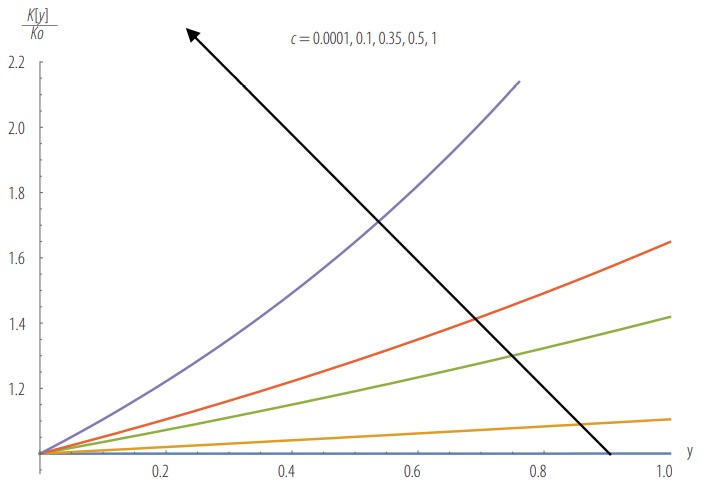
Exponential permeability variation as a function of fitting factor c.
Fig. 2 illustrates the dimensionless permeability function, scaled by the average permeability, as a function of the fitting parameter. When the fitting parameter c approaches zero, the permeability approaches a constant value. At higher values of c, higher values of the permeability function are obtained. This behaviour is expected in light of the exponential nature of the chosen permeability function. It also emphasizes the important role of the fitting parameter in controlling variations in permeability.
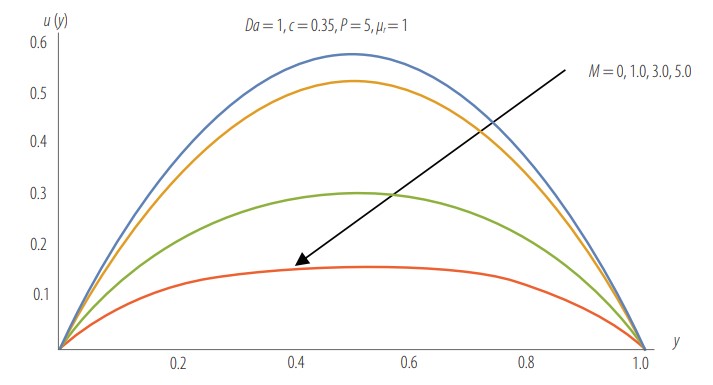
Velocity profile as a function of M and fixed values of Da, c, P, and µr.
Fig. 3 illustrates the velocity as a function of Hartman number, M, and fixed values of Da, c, P, and µr When M increases, the velocity decreases, thus indicating the slowing effect the magnetic number has on velocity.
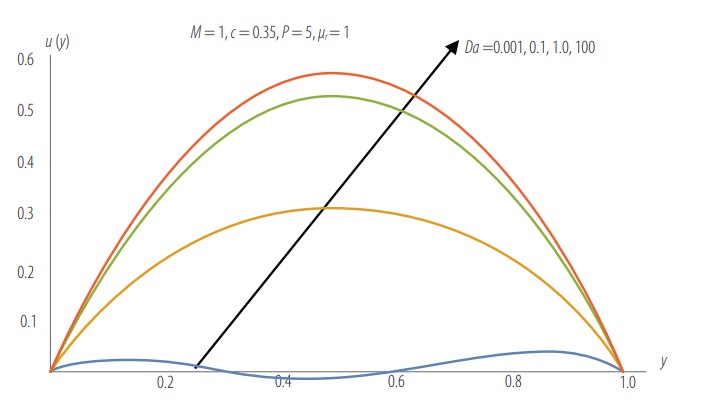
Velocity profile as a function of Da and fixed values of M, c, P, and µr.
Fig. 4 illustrates velocity as a function of Darcy number, Da, and fixed values of M, c, P and µr. The effect of increasing Darcy number is of course to increase velocity due to the fact that permeability increases with Darcy number. For very low values of Da, the velocity becomes very small and starts approaching zero as we approach the solid. We point out here that Tables 1 and 2 do not show . This might be attributed to the fact that solid boundary is a computed quantity, hence computed within the error tolerance of the computation procedure, or machine zero.
The volumetric flow rate given by Eq. (12) is the area bounded by the velocity curves and the y-axis. Based on the velocity behavior in Fig. 3, Fig. 4, and Fig. 5, we conclude that this bounded area (hence the volumetric flow rate) increases with decreasing M, increases with increasing Da, and decreases with increasing.
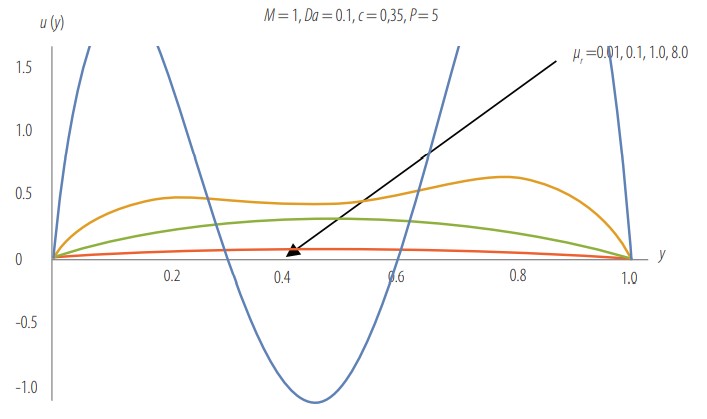
FIGURE 5. Velocity profile as a function of µr and fixed values of M, Da, c, and P.
Fig. 5 illustrates velocity as a function of µr and fixed values of M, Da, c, and P. With increasing µr, Fig. 5 shows that velocity decreases. This might be due to the increase in the shear term in Eq. (9). For low values of µr , the shear term becomes insignificant, and Eq. (7) behaves like a Darcy equation. According to the work of Ochoa-Tapia and Whitaker [60], the viscosity ratio is equal to the reciprocal of the porosity of the porous medium. A value of µr = 0.01 implies that porosity is 100% or unity. This is a physical impossibility since a porosity of unity implies the absence of a porous matrix and contradicts the Darcy-like behavior when µr is small. On the other hand, Nield [61] indicated that the Brinkman equation cannot be rigorously justified except when the porosity is close to unity and the self-consistent formulation of Brinkman breaks down when the porosity is less than 0.6. This translates into the critical value of µr ≈1.67. For larger values of µr, Fig. 5 shows that the velocity decreases drastically until it vanishes when this value is higher than 8. While the above indicates that , Givler and Altobelli [62] used a porosity value of ϕ = 0.972 for water flow in a porous medium made of rigid foam, which corresponds to μr ≈ 1.03.
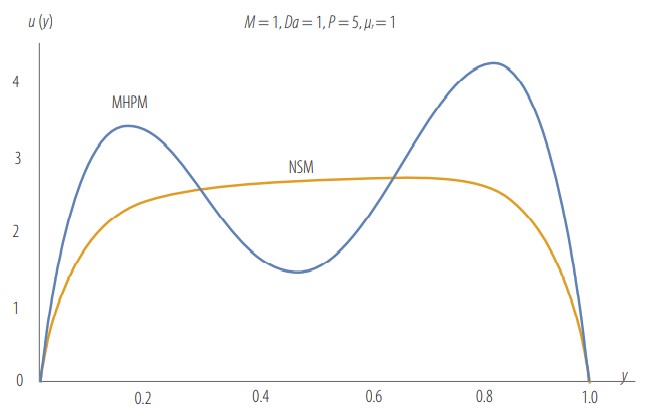
Comparison of the velocity profile between MHPM and NSM at low µr.
Fig. 6 supports the analysis obtained using Fig. 5 and provides a comparison of the velocity profiles obtained using the MHPM and the NSM. At viscosity ratio value of µr = 0.01, the velocity profile obtained using MHPM loses its accuracy, which indicates that the velocity obtained by MHPM is valid for µr > 0.01.
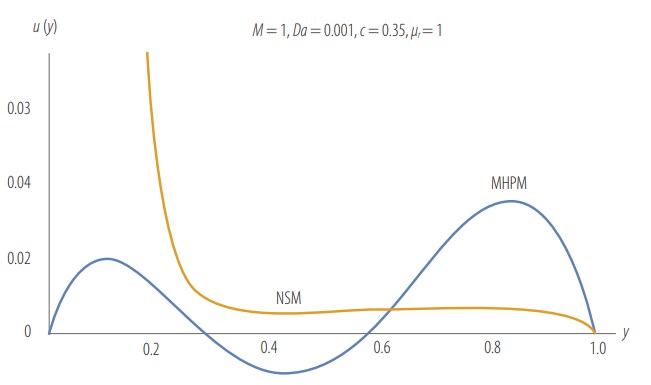
Comparison of the velocity profile between MHPM and NSM at low Da.
In Fig. 7 we observe that for low values of Da, (Da < 0.001) the Brinkman model for the MHD fluid flow through a porous medium with exponentially variable permeability is not valid, by comparing the results of the two approximation methods used in this work. This might be due to the fact that for small values of Da, permeability is low, and the flow becomes Darcy-like, thus resulting in insignificant Brinkman effects.
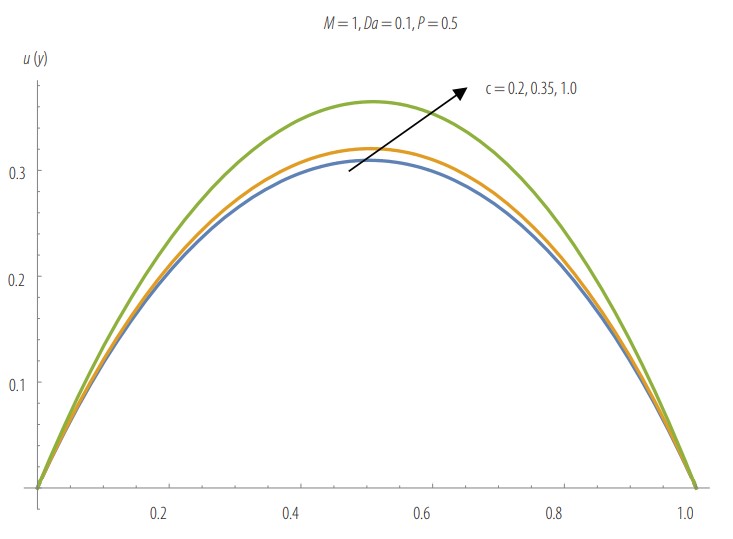
Velocity profile as a function of c and fixed values of M, Da, P, and µr.
Fig. 8 illustrates the velocity as a function of c for fixed values of M, Da, P and µr .Velocity increases with increasing values of fitting parameter, c, for c > 0.2. When c < 0.2 the computed velocity is unreliable due to low permeability. Low permeability results in Darcy-like behavior, while the Brinkman effects become insignificant.
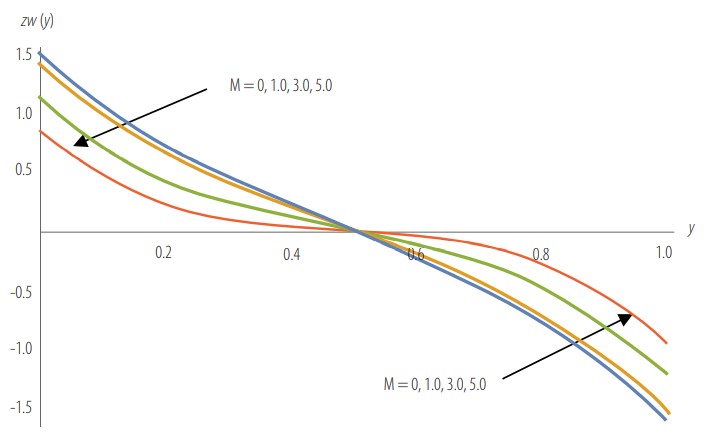
Wall shear stress as a function of for P = 5,
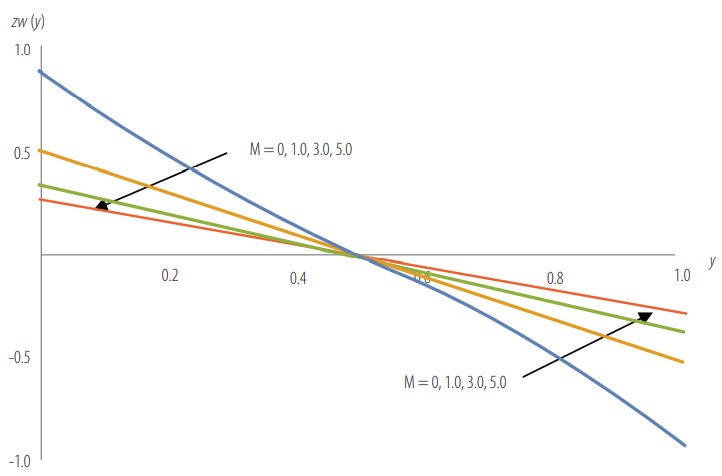
Dimensionless wall shear stress Tw (y) as a function of µr for P = 5, Da =1, M=1, and c=0.35.
CONCLUSIONS AND RECOMMENDATIONS
An analysis of the flow of MHD fluid through a porous medium of increasing exponential permeability has been carried out in order to provide a baseline study and a benchmark with which future analysis of flow through variable permeability media can be compared.
The MHPM was used to find the solution of the Darcy-Brinkman model, under the no-slip boundary condition. Effects of medium and flow parameters on the velocity distribution, volumetric flow rate and the wall shear stress have been analyzed.
Three parameters have been examined with special interest: c, Da, and µr. Part of the analysis is to define the limit of the viscosity ratio in the model of Darcy-Brinkman. Because of the foregoing, the validity of the modified Brinkman's equation for the MHD fluid flow through a porous medium with exponentially variable permeability should be further evaluated to confirm if indeed the viscosity ratio depends solely on porosity as stated by Ochoa-Tapia and Whitaker [60] or if other factors would be included such as tortuosity as indicated by other authors (cf. Liu and Masliyah [63] and the references therein).
Based on the results and analysis of this work, the following conclusions can be drawn:
Of the three parameters, c, Da, and µr, the two most critical parameters are Da and µr. Low values of these parameters result in the Darcy-Brinkman equation behaving like a Darcy equation. Brinkman’s viscous shear effects become insignificant.
The permeability fitting parameter plays an important role in controlling variations in permeability.
A wide range of 0.01 < µr < 1.67 has been suggested based on velocity profiles obtained in this work. Again, low values of µr hamper the solutions obtained by the MHPM.
Results obtained using MHPM have been validated using a Numerical Shooting Method. There is an agreement of up to six significant figures, and a maximum absolute error not exceeding 5x10-5, between the velocity values computed using MHPM and NSM.
As the magnetic number M increases, the velocity decreases, thus indicating the slowing effect the magnetic number has on velocity.
Increasing Darcy number implies increasing permeability, which in turn results in increasing flow velocity.
Volumetric flow rate increases with decreasing M, increases with increasing Da, and decreases with increasing µr.
When M increases, Tw decreases in the range 0 ≤ y < 0.5 and increases in the range 0.5 < y ≤ 1.
When µr increases, Tw decreases in the range 0 ≤ y < 0.5 and increases in the range 0.5 < y ≤ 1.
Based on results and analysis of this work, and the conclusions drawn above, the following are recommendations that point to the need for future work in this area of research:
Permeability distribution influences model equations’ behavior and solution. It is imperative to provide further studies that employ other permeability functions for the sake of comparison.
Darcy number is of greatest influence on the flow quantities, for a given permeability distribution. Low values of Da render Brinkman’s shear effects insignificant. It is imperative to determine, for a given permeability distribution, the range of values that Da can assume.
The need for a methodology to determine accurate values of µr, rather than ranges, remains an outstanding research problem without consensus. Matters become more complicated when MHD effects are taken into account. It is therefore imperative for future work to consider a realistic method for estimating µr.
DISCUSSION
In this section, we provide insight on this work in light of state-of-the-art knowledge in the field.
At the outset, we wish to emphasize that while research work in MHD flow through porous media has received considerable attention for more than half a century, and continues to receive attention due to its important applications, most of the work in this field has been centered around flow through constant permeability porous media. However, impetus is being generated and focus is shifting towards flow through variable permeability media, as is witnessed by the current work. This might be due in part to recent developments in variable permeability models, as discussed in the introduction section of this work, where most of the available models have been documented.
Literature Survey
In order to initiate this work, the authors have carried out a thorough literature survey in the areas of MHD flow, MHD flow through porous media, MHD flow through porous media with variable permeability and porosity, and variable permeability porous layers. The most relevant bibliographic data to the current work are listed in the references section.
The introduction section follows the historical interest of MHD flow between parallel plates from the inception of the problem with the works of Hartmann and Lazarus [32] and Jeffrey [33] of the mid-1930’s to the work of Rudraiah et.al. [48], mid-1970’s work on MHD flow through porous media, to the 21st century work of Geindreau and Auriault [47], in which MHD equations of flow through porous media have been cast in their final and complete form.
The literature survey also included the most relevant and available models of variable permeability media and the specific MHD flow problems that have been considered in the literature. This culminated in a selection of a most relevant exponential permeability model that serves the objectives of this work.
Model Equations
Governing equations used in this work are the state-of-the-art comprehensive model of MHD flow through porous media that was initiated by Rudraiah et.al. [48] and thoroughly analyzed and derived by Geindreau and Auriault [47]. These model equations were used in the formulation of the problem considered in this work, and an exponential permeability function has been incorporated in the model equations.
Solution to Model Equations
Generally speaking, many problems in theoretical mechanics lend themselves to three types of solution methodologies: (i) Analytical solutions; (ii) Numerical solutions; and (iii) Special purpose methodologies.
The current problem is differential equations based. The authors are pleased to have been able to provide solutions using the three methodologies. An analytic solution has been provided in terms of Bessel functions. Alas, the complicated nature of these functions rendered the solution impractical and hardly tractable. A numerical solution based on Numerical Shooting Method (NSM) has also been provided to validate the solution obtained using the efficient technique of Modified Homotopy Perturbation Method (MHPM). Agreement between the NSM and MHPM methods has been discussed in this work and assured us of the correctness of solutions obtained.
Presentation of Results
Clear graphs and tables have been used to present our findings in this work. We presented a thorough and accurate account of what the data told us. An objective of the work has been to study the effects of flow and medium parameters on velocity, volumetric flow rate, and wall shear stress. We believe, based on the conclusions drawn, that this objective has been achieved.
Interpretation of Findings
Data obtained in this work supported some critical conclusions of the effects of the parameters and limitations of the methodologies used. Critical ranges of some parameters have been identified. They also point to the need for continuing efforts in this research area. We have searched for some partial answers, but now we must research in order to improve on the obtained solutions by considering further models that better predict a more accurate behavior, or else to provide methodologies that overcome some of the limitations that we have identified.
Overall Contribution and Significance
We believe that our modest contribution is significant to the advancement of state-of- the-art knowledge in the field and presents a baseline and a bench mark with which further contributions can be compared.
References
[1] Nield, D. A., & Bejan, A. (2006). Mechanics of Fluid Flow Through Porous Media. In D. A. Nield, & A. Bejan, Convection in Porous Media (3 ed., pp. 14-16). USA: Springer.
[2] Rudraiah, N. (1986). Flow past porous layers and their stability. In N. P. Cheremisinoff (Ed.), Encyclopedia of Fluid Mechanics, Slurry Flow Technology (Vol. 8, pp. 567-647). Houston, Texas, USA: Gulf Publishing. Retrieved from https://archive.org/details/in.ernet.dli.2015.148666/page/n3/mode/2up
[3] Alzahrani, S., Gadoura, I., & Hamdan, M. (2016, May-June). Nield- Kuznetsov Functions of the First- and Second Kind. IOSR Journal of Applied Physics, 8(3 Version III), 47-56. Retrieved from http://www.iosrjournals.org/iosr-jap/papers/Vol8-issue3/Version-3/H0803034756.pdf
[4] Attia, H., & Abdeen, M. (2012). Unsteady MHD Flow and Heat Transfer Between Parallel Porous Plates with Exponential Decaying Pressure Gradient. Kragujevac Journal of Science(34), 15-22. Retrieved from https://www.pmf.kg.ac.rs/KJS/images/volumes/vol34/kjs34attiaabdeen15revision.pdf
[5] Barcena, C., Sra, A., & Gao, J. (2009). Applications of Magnetic Nanoparticles in Biomedicine. In J. Ping Liu, E. Fullerton, O. Gutfleisch, & D. Sellmyer (Eds.), Nanoscale Magnetic Materials and Applications (pp. 591-626). Springer. doi: https://doi.org/10.1007/978-0-387-85600-1
[6] Mishra, S., Baag, S., Dash, G., & Acharya, M. (2019). Numerical approach to MHD flow of power-law fluid on a stretching sheet with non-uniform heat source. Nonlinear Engineering, 9(1), 81-93. doi: https://doi.org/10.1515/nleng-2018-0026
[7] Shehzad, S., & Hayat, T. A. (2015). Influence of convective heat and mass conditions in MHD flow of nanofluid. Bull. PolishAcadSc. Tech. Sci., 63(2), 465-474. doi: https://doi.org/10.1515/bpasts-2015-0053
[8] Hamdan, M., Kamel, M., & Siyyam, H. (2009). A permeability function for Brinkman’s equation. Proceedings of the 11th Conf. on Mathematical Methods, System Theory and Control (pp. 198-205). WSEAS Publications. Retrieved from https://pdfs.semanticscholar.org/b2b7/8e0741d09e511c6a461d3b22a01a5d4151e7.pdf
[9] Brinkman, H. C. (1947). A Calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Scientific Res., A1, 27-34. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.454.3769&rep=rep1&type=pdf
[10] Hamdan, M., & Kamel, M. (2011). Flow through Variable Permeability Porous Layers. Adv. Theor. Appl. Mech., 4(3), 135 - 145. Retrieved from http://m-hikari.com/atam/atam2011/atam1-4-2011/hamdanATAM1-4-2011-2.pdf
[11] Auriault, J.-L. (2009, September). On the Domain of Validity of Brinkman’s Equation. Transport in Porous Media, 79(2), 215-223. doi: https://doi.org/10.1007/s11242-008-9308-7
[12] Parvazinia, M., Nassehi, V., Wakeman, R. J., & Ghoreishy, M. H. (2006, April). Finite element modelling of flow through a porous medium between two parallel plates using the Brinkman equation. Transport in Porous Media(63), 71-90. doi: https://doi.org/10.1007/s11242-005-2721-2
[13] Nield, D. A. (1991, September). The Limitations of the Brinkman-Forchheimer equation in modeling flow in a saturated porous medium and at an interface. International Journal of Heat and Fluid Flow, 12(3), 269-272. doi: https://doi.org/10.1016/0142-727X(91)90062-Z
[14] Sahraoui, M., & Kaviany, M. (1992). Slip and no-slip velocity boundary conditions at interface of porous, plain media. International Journal of Heat and Mass Transfer, 35(4), 927-943. doi: http://dx.doi.org/10.1016/0017-9310(92)90258-T
[15] Kaviany, M. (1995). Part I Single Phase Flow. Fluid Mechanics. In M. Kaviany, Principles of Heat Transfer inPorous Media (2 ed., pp. 95-100). Spinger, Mechanical Engineering Series. doi: https://doi.org/10.1007/978-1-4684-0412-8
[16] Lundgren, T. S. (1972). Slow Flow Through Stationary Random Beds and Suspensions of Spheres. Journal of Fluid Mechanics(51), 273-299. doi: http://dx.doi.org/10.1017/S002211207200120X
[17] Cheng, A. H.-D. (1984, July). Darcy’s Flow With Variable Permeability: A Boundary Integral Solution. (A. G. Union, Ed.) Water Resources Research, 20(7), 980-984. doi: https://doi.org/10.1029/WR020i007p00980
[18] Hamdan, M. H., & Abu Zaytoon, M. S. (2017, May-June). Flow over a Finite Forchheimer Porous Layer with Variable Permeability. IOSR Journal of Mechanical and Civil Engineering, 14(3), 15-22. doi: https://doi.org/10.9790/1684-1403041522
[19] Elaiw, A., Ibrahim, F., & Bakr, A. (2009). Variable permeability and inertia effect on vortex instability of natural convection flow over horizontal permeable plates in porous media. Commun Nonlinear Sci Numer Simulat, 14, 21902201. doi: https://doi.org/10.1016/j.cnsns.2008.06.022
[20] Hassanien, I. (2003). Variable permeability effects on mixed convection along a vertical wedge embedded in a porous medium with variable surface heat flux. Applied Mathematics and Computation, 138, 41-59. doi: https://doi.org/S0096-3003(02)00098-X
[21] Hassanien, I., Salama, A., & Elaiw, A. (2003, December). Variable permeability effect on vortex instability of mixed convection flow in a semi-infinite porous medium bounded by a horizontal surface. Applied Mathematics and Computation, 146(2-3), 829-847. doi: https://doi.org/10.1016/S0096-3003(02)00635-5
[22] Jang, J.-Y., & Chen, J.-L. (1993). Variable porosity effect on vortex instability of a horizontal mixed convection flow in a saturated porous medium. International Journal of Heat and Mass Transfer, 36(6), 1573-1582.
[23] Chandrasekhara, B., Namboodiri, P., & Hanumanthappa, A. (1984, March 01). Similarity solutions for buoyancy induced flows in a saturated porous medium adjacent to impermeable horizontal surfaces. Wärme-und Stoffübertragung, 18(1), 17-23.
[24] Abu Zaytoon, M. (2015). Flow through and over porous layers of variable thickness and permeability. Canada: University of New Brunswick. Retrieved from https://unbscholar.lib.unb.ca/islandora/object/unbscholar%3A7625
[25] Chandrasekhara, B., Hanumanthappa, A., & Chandranna, S. (1984, January 01). Influence of Variable Permeability on the Basic Flows in Porous Media. Indian Journal of Technology, 22(8), 281-283.
[26] Goldstein, R., Ibele, W., Patankar, S., Simon, T., Kuehn, T., Strykowski, P., . . . Srinivasan, V. (2006). Heat transfer—A review of 2003 literature. International Journal of Heat and Mass Transfer, 49, 451-534. doi: https://doi.org/10.1016/j.ijheatmasstransfer.2005.11.001
[27] Schiffman, R., & Gibson, R. (1964). Consolidation of Nonhomogeneous Clay Layers. Journal of the Soil Mechanics and Foundations Division, 90(5), 1-30.
[28] Mahmoud, M. S., & Deresiewicz, H. (1980, January-March). Settlement of inhomogeneous consolidating soils—I: The single-drained layer under confined compression. International Journal for Numerical and Analytical Methods in Geomechanics, 4(1), 57-72. doi: https://doi.org/10.1002/nag.1610040105
[29] Rees, D. A., & Pop, I. (2000). Vertical free convection in a porous medium with variable permeability effects. International Journal of Heat and Mass Transfer, 43, 2565-2571. Retrieved from https://people.bath.ac.uk/ensdasr/PAPERS/PAPERS.bho/paper51.pdf
[30] Alloui, Z., Bennacer, R., & Vasseur, P. (2009, June). Variable permeability effect on convection in binary mixtures saturating a porous layer. Heat and Mass Transfer, 45(8), 1117-1127. doi: https://doi.org/10.1007/s00231-009-0488-7
[31] Choukairy, K., & Bennacer, R. (2012). Numerical and Analytical Analysis of the Thermosolutal Convection in an Heterogeneous Porous Cavity. FDMP-Fluid Dynamics & Materials Processing, 8(2), 155-172. doi: https://doi.org/10.3970/fdmp.2012.008.155
[32] Hartmann, J., & Lazarus, F. (1937). Experimental investigations on the flow of mercury in a homogeneous magnetic field. Matematisk-fysiske meddelelser Kongelige Danske Videnskabernes Selskab, 15(7), 1-45.
[33] He, J.-H. (2003, February 15). Homotopy perturbation method: A new nonlinear analytical technique. Applied Mathematics and Computation, 135(1), 73-79. doi: https://doi.org/10.1016/S0096-3003(01)00312-5
[34] Müller, U., & Bühler, L. (2001). Analytical solutions for MHD channel flow. In U. Müller, & L. Bühler, Magnetofluiddynamics in Channels and Containers (pp. 37-56). Berlin-Heidelberg, Germany: Springer.
[35] Rothmayer, A. P. (2014). Magnetohydrodynamic channel flows with weak transverse magnetic fields. Phil. Trans. R. Soc. A. (372), 1-12. doi: https://doi.org/10.1098/rsta.2013.0344
[36] Awartani, M., & Hamdan, M. (2005, October). Fully developed flow through a porous channel bounded by flat plates. Applied Mathematics and Computation, 2(169), 749-757. doi: https://doi.org/10.1016/j.amc.2004.09.087
[37] Fu, W.-S., Huang, H.-C., & Liou, W.-Y. (1996). Thermal enhancement in laminar channel flow with a porous block. International Journal of Heat and Mass Transfer, 39(10), 2165 2175.
[38] Harwin, D. A. (2007). Flows in Porous Channels. Bath, United Kingdom: University of Bath. Retrieved from https://people.bath.ac.uk/masjde/Theses/Thesis-Harwin.pdf
[39] Kaviany, M. (1985). Laminar flow through a porous channel bounded by isothermal parallel plates. International Journal of Heat and Mass Transfer, 28(4), 851-858.
[40] Liu, S., Afacan, A., & Masliyah, J. (1994). Steady Incompressible Laminar Flow in Porous Media. Chmdml Engineering Science, 3565-3586.
[41] Pillai, K., Varma, S., & Babu, M. S. (1987, August). Aligned magnetic effects through varying permeable bed. Proc. Indian Acad. Sci. (Math. Sci.), 96(1), 61-69. Retrieved from https://www.ias.ac.in/article/fulltext/pmsc/096/01/0061-0069
[42] Sinha, A., & Chadda, G. (1984, September). Steady Laminar Viscous Flow Down an Open Inclined Channel with a Bed of Varying Permeability. Indian J. Pure Appl. Math., 15(9), 1004-1013. Retrieved from https://insa.nic.in/writereaddata/UpLoadedFiles/IJPAM/20005a6e_1004.pdf
[43] Narasimha Murthy, S., & Feyen, J. (1989). Influence of variable permeability on the dispersion of a chemically reacting solute in porous media. International Journal of Engineering Science, 27(12), 1661-1671. doi: https://doi.org/10.1016/0020-7225(89)90159-6
[44] Mathew, S. (2005). Mathematical Analysis. In S. Mathew, MHD Convective Heat Transfer Through a Porous Medium in a Vertical Channel with periodic permeability (pp. 7-10). India: Sri Krishnadevaraya University Anantapur. Retrieved from http://hdl.handle.net/10603/64940
[45] Srivastava, B., & Deo, S. (2013, May). Effect of magnetic field on the viscous fluid flow in a channel filled with porous medium of variable permeability. Applied Mathematics and Computation, 219(17), 8959-8964. doi: https://doi.org/10.1016/j.amc.2013.03.065
[46] He, J. H. (2008). Recent Development of the Homotopy Perturbation Method. Topological Methods in Nonlinear Analysis, 31, 205-209. Retrieved from https://projecteuclid.org/download/pdf_1/euclid.tmna/1463150264
[47] Geindreau, C., & Auriault, J.-L. (2002, September). Magnetohydrodynamic flows in porous media. Journal of Fluid Mechanics, 466, 343-363. doi: https://doi.org/10.1017/S0022112002001404
[48] Rudraiah, N., Ramaiah, B., & Rajasekhar, B. (1975, January). Hartmann flow over a permeable bed. International Journal of Engineering Science, 13(1), 1-24. doi: https://doi.org/10.1016/0020-7225(75)90070-1
[49] Merabet, N., Siyyam, H., & Hamdan, M. (2008). Analytical approach to the Darcy-Lapwood-Brinkman equation. Applied Mathematics and Computation, 196, 679-685. doi: https://doi.org/10.1016/j.amc.2007.07.003
[50] Abu Zaytoon, M., Alderson, T., & Hamdan, M. (2016, June). Flow through a Layered Porous Configuration with Generalized Variable Permeability. International. Journal of Enhanced Research in Science, Technology & Engineering, 5(6), 1-21. Retrieved from http://www.erpublications.com/uploaded_files/download/download_05_06_2016_16_55_43.pdf
[51] Seyf, H., & Rassoulinejad-Mousavi, S. (2011). He’s Homotopy Method for Investigation of Flow and Heat Transfer in a Fluid Saturated Porous Medium. World Applied Sciences Journal, 15(12), 1791-1799. Retrieved from http://www.idosi.org/wasj/wasj15(12)11/21.pdf
[52] He, J. H. (2006). New interpretation of homotopy perturbation. International Journal of Modern Physics B, 20(18), 2561-2568. Retrieved from https://works.bepress.com/ji_huan_he/3/
[53] He, J. H. (2006, April). Some Asymptotic Methods for Strongly Nonlinear Equations. International Journal of Modern Physics B, 20(10), 1141-1199. doi: https://doi.org/10.1142/S0217979206033796
[54] He, J.-H. (1999, August). Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering, 178(3-4), 257-262. doi: https://doi.org/10.1016/S0045-7825(99)00018-3
[55] He, J.-H. (2000). A coupling method of a homotopy technique and a perturbation technique for non-linear problems. International Journal of Non-Linear Mechanics, 35(1), 37-43. doi: https://doi.org/10.1016/S0020-7462(98)00085-7
[56] He, J.-H. (2003, February 15). Homotopy perturbation method: A new nonlinear analytical technique. Applied Mathematics and Computation, 135(1), 73-79. doi: https://doi.org/10.1016/S0096-3003(01)00312-5
[57] He, J.-H. (2004, March 30). The homotopy perturbation method for non-linear oscillators with discontinuities. Applied Mathematics and Computation, 151(1), 287-292. doi: https://doi.org/10.1016/S0096-3003(03)00341-2
[58] Jazbi, B., & Moini, M. (2008, February). Application of He’s homotopy perturbation method for Schrodinger equation. Iranian Journal of Mathematical Sciences and Informatics, 3(2), 13-19. doi: https://doi.org/10.7058/ijmsi.2008.02.002
[59] Usman, M., Naheed, Z., Nazir, A., & Mohyud-Din, S. (2014, July). On MHD flow of an incompressible viscous fluid. Journal of the Egyptian Mathematical Society, 22(2), 214-219. doi: https://doi.org/10.1016/j.joems.2013.07.003
[60] Ochoa-Tapia, J. A., & Whitaker, S. (1995, September 1). Momentum transfer at the boundary between a porous medium and a homogeneous fluid — I. Theoretical development. International Journal of Heat and Mass Transfer, 38(14), 2635-2646. doi: https://doi.org/10.1016/0017-9310(94)00346-W
[61] Nield, D. (2000). Modelling Fluid Flow and Heat Transfer in a Saturated Porous Medium. Journal of Applied Mathematics & Decision Sciences, 4(2), 165-173. Retrieved from http://www.kurims.kyoto-u.ac.jp/EMIS/journals/HOA/JAMDS/Volume4_2/173.pdf
[62] Givler, R., & Altobelli, S. (1994, January 10). A determination of the effective viscosity for the Brinkman-Forchheimer flow model. Journal of Fluid Mechanics, 258, 355-370. doi: https://doi.org/10.1017/S0022112094003368
[63] Liu, S., & Masliyah, J. (2005). Dispersion in Porous Media. In K. Vafai (Ed.), Handbook of Porous Media (2 ed., pp. 110111). Boca Raton, Florida, USA: Taylor & Francis.
Additional information
ACKNOWLEDGMENTS: The authors wish to acknowledge
with thanks the thoughtful suggestions, which enhanced readability and content
of this manuscript, made by the reviewers of this work.
AUTHOR'S CONTRIBUTIONS: Silva-Zea:
Statement of the problem, references, mathematical model, method of solution.
Project administration. Hamdan: Introduction, mathematical analysis, reviewer
of the text, discussion of results, conclusions, and references. Erazo-Bone: abstract, plots and tables. Chuchuca-Aguilar:
Introduction, state of the art, references. Escobar-Segovia: Formatting the
text, plots, sketch, and tables.
CONFLICTS OF INTEREST: The authors declare that there
is no conflict of interests regarding the publication of this paper.