Cálculo fraccionario para ecuaciones diferenciales
Fractional calculus for differential equations
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
Recepción: 20 Agosto 2020
Aprobación: 24 Diciembre 2020
Resumen: En el presente trabajo se estudian dos metodologías distintas para la resolución de ecuaciones diferenciales parciales fraccionarias. La primera metodología consiste en usar la transformada de Laplace. Para esto, se propone una solución de tipo producto de funciones la cual nos permite reducir el problema a la resolución de dos ecuaciones diferenciales ordinarias fraccionarias y mediante el uso de la transformada de Laplace se obtiene una solución para las ecuaciones diferenciales obtenidas a partir del producto de funciones. Por otro lado, en la segunda metodología se asume que nuestras funciones admiten derivadas sumables y se realiza integración directa sobre la ecuacion diferencial parcial fraccionaria. Posteriormente se toma la transformada de Laplace del resultado obtenido y se llega a una ecuación de tipo Volterra de segundo orden. Finalmente, dada la convergencia de las integrales y funciones se simplifica la solución y se toma la transformada inversa del resultado previamente obtenido. Para finalizar el trabajo, se realiza una discusion sobre las limitaciones y libertades de ambos métodos.
Palabras clave: Derivada Fraccionaria de Riemann-Liouville, Transformada de Laplace, Ecuaciones Diferenciales Fraccionarias, Ecuaciones Integrales, Derivada sumable, Ecuación integral de Volterra.
Abstract: The present work presents two methodologies to find solutions to fractional partial differential equations. The first methodology is an approach using the Laplace transform. In order to do that, a solution as a product of functions is proposed in order to separate the fractional partial differential equation in two fractional ordinary differential equations. Then the solutions of the fractional ordinary differential equations using the Laplace transform are found. In the second methodology, we suppose that our functions admits a fractional summable derivative in order to integrate them. Then, using the Laplace transform, a Volterra integral equation of second order is found. Using the convergence of the integral and functions the solution is simplified in order to take the inverse Laplace transform of it. Finally, a discussion about the freedoms and restrictions of two methods is made.
Keywords: Fractional differential equation, Riemann-Liouville fractional derivative, Riemann-Liouville fractional integral, Laplace Transform, Integral Equation, Summable Derivative, Volterra Integral equation.
INTRODUCCIÓN
El modelado matemático consiste en traducir problemas relevantes de la industria y del día a día a problemas matemáticos mediante procedimientos teóricos o numéricos [1]. En particular, el modelado de fenómenos físicos y químicos muchas veces nos lleva al planteamiento de ecuaciones diferenciales que pueden ser descritos mediante una función de una o más variables [2]. La idea del modelado es poder predecir y analizar el comportamiento del sistema; sin embargo, el modelado no describe en su plenitud el fenómeno que deseamos estudiar y una mejor descripción del fenómeno involucra un incremento en la complejidad del modelo [3]. Por ejemplo, consideremos un sistema masa resorte en el vacío, también conocido como oscilador armónico simple. A pesar de que el oscilador armónico nos ayuda a describir una gran variedad de sistemas, en el modelado con el oscilador armónico no se consideran una gran cantidad de parámetros que pueden afectar a la descripción del mismo, como lo es la fricción y otros. Si consideramos la fricción dentro de nuestro sistema masa resorte, obtenemos un movimiento armónico amortiguado cuya solución es más compleja y, de esta forma, conforme vamos considerando elementos de nuestros sistemas que pueden o no tener impacto en el mismo, nuestro modelo se va complicando y es más difícil de obtener una ecuación que lo describa.
En los últimos años, la implementación de derivadas de orden no entero, es decir derivadas de la forma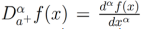 tal que
tal que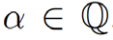 , ha tenido un gran impacto en la descripción de sistemas relacionados con interacciones de largo alcance y sistemas con memoria descrita por una potencia [4]. En particular, el cálculo fraccionario ha descrito con gran exactitud fenómenos relacionados al amortiguamiento [5]. Como consecuencia, el cálculo fraccionario nos ha permitido investigar la elasticidad en materiales desde una nueva perspectiva. Para esto se utilizan modelos fraccionarios no locales de materiales elásticos, en los cuales el kernel
, ha tenido un gran impacto en la descripción de sistemas relacionados con interacciones de largo alcance y sistemas con memoria descrita por una potencia [4]. En particular, el cálculo fraccionario ha descrito con gran exactitud fenómenos relacionados al amortiguamiento [5]. Como consecuencia, el cálculo fraccionario nos ha permitido investigar la elasticidad en materiales desde una nueva perspectiva. Para esto se utilizan modelos fraccionarios no locales de materiales elásticos, en los cuales el kernel 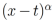 de las integrales fraccionarias describen un nuevo comportamiento mecánico del material [6]. En el caso de sistemas visco-elásticos, como las arterias, la potencia del kernel de la derivada fraccionaria permite pasar de sistemas completamente elásticos a sistemas viscosos [7]. Para ilustrar esta última idea, notemos que las arterias suelen ser modeladas mediante el uso de Dashpots, los cuales son obtenidos a partir de la ley de Hook y son descritos por la siguiente ecuación:
de las integrales fraccionarias describen un nuevo comportamiento mecánico del material [6]. En el caso de sistemas visco-elásticos, como las arterias, la potencia del kernel de la derivada fraccionaria permite pasar de sistemas completamente elásticos a sistemas viscosos [7]. Para ilustrar esta última idea, notemos que las arterias suelen ser modeladas mediante el uso de Dashpots, los cuales son obtenidos a partir de la ley de Hook y son descritos por la siguiente ecuación:
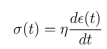
donde es el impulso aplicado, es la viscosidad y es la presión. Los Dashpots describen un comportamiento completamente viscoso, por lo cual no se obtiene una descripción adecuada de las arterias ya que estos vasos sanguíneos se comportan como resortes. Como propuesta ante esta dificultad se introducen los Spring-pot, los cuales se definen como
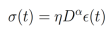
donde es la derivada fraccionaria de orden , tal que . Este elemento interpola un resorte ( = 0) y un Dashpot ( = 1) [7], permitiéndonos de esta forma, describir el comportamiento de las arterias de una forma elegante y sencilla.
La versión fraccionaria del operador de Laplace también ha tenido una gran aplicación en distintas áreas como mecánica y electrostática, inclusive en el marco de la probabilidad, eSm'e donde actúa como generador de procesos de Levi estable [8]. En el área económica, las '"quenas derivadas de orden no entero se han usado en procesos económicos dinámicos, en el cual el orden fraccionario de la derivada modela la memoria del sistema, parámetro que suele ser olvidado en la mayoría de los modelos [9].
Las derivadas fraccionarias cuentan con propiedades inusuales, como la violación de la regla de Leibniz (ley del producto) y de la regla de la cadena (derivada de la composición de dos funciones ) [9]. Si bien es cierto que estas propiedades nos ayudan a describir características complejas de sistemas dinámicos, dichas propiedades llegan a presentar más dificultad en la resolución de ecuaciones diferenciales fraccionarias, por lo cual se han utilizado diferentes enfoques para intentar hallar una solución analítica de ecuaciones diferenciales fraccionarias como por ejemplo: la aplicación directa de la transformada de Laplace, el uso de operadores y el método de análisis con homotopía [10].
En este trabajo, se presentan dos métodos de resolución de ecuaciones diferenciales parciales fraccionarias. En el primer método, se estudia la transformada de Laplace de la derivada fraccionaria de Riemann-Liouville. Posteriormente, proponiendo una solución de tipo producto de funciones, se separa la ecuación diferencial parcial fraccionaria en dos ecuaciones diferenciales ordinarias fraccionarias [11, 12] las cuales son resueltas mediante el uso de la transformada de Laplace [13], de tal forma que la solución de la ecuación diferencial parcial fraccionaria original pueda ser expresada como producto de las soluciones de las dos ecuaciones diferenciales ordinarias fraccionarias. En la segunda metodología, se asume que nuestra ecuación admite derivadas sumables, lo cual nos permite integrar en ambos lados de la ecuación diferencial parcial fraccionaria y, utilizando las relaciones entre la derivada e integral fraccionaria de Riemann-Liouville, se llega a una ecuación Laplace transformable[14]. Tomando la transformada de Laplace del resultado previamente obtenido y reorganizando los términos se llega a una ecuación de Volterra de segunda especie, que garantiza una única solución[15].
HISTORIA DEL CÁLCULO FRACCIONARIO EN R
El origen del cálculo fraccionario data de 1695, año en el que el marqués de L'Hopital mediante una carta, preguntó a Leibniz cual sería el resultado de con 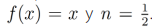 . A lo que Leibniz respondió que “esto conduciría aparentemente a una paradoja de la cual algún día serán extraídas consecuencias muy útiles”. Con estas palabras nació el cálculo fraccionario [16]. A partir de ese momento, muchos matemáticos contribuyeron al desarollo del cálculo de orden no entero. En 1730, Euler desarrolló trabajos sobre la interpolación entre derivadas de orden entero. En 1812, Laplace definió la derivada fraccionaria en base a integrales. Posteriormente en 1819, el matemático francés Lacroix discutió por primera vez la derivada fraccionaria en un libro de cálculo [17]. A partir de
. A lo que Leibniz respondió que “esto conduciría aparentemente a una paradoja de la cual algún día serán extraídas consecuencias muy útiles”. Con estas palabras nació el cálculo fraccionario [16]. A partir de ese momento, muchos matemáticos contribuyeron al desarollo del cálculo de orden no entero. En 1730, Euler desarrolló trabajos sobre la interpolación entre derivadas de orden entero. En 1812, Laplace definió la derivada fraccionaria en base a integrales. Posteriormente en 1819, el matemático francés Lacroix discutió por primera vez la derivada fraccionaria en un libro de cálculo [17]. A partir de
Lacroix determinó que la n-esima derivada de estaría dada por
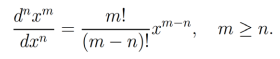 (1)
(1)Con la cual, para n=1/2 y m=1 se obtiene el siguiente resultado
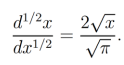
De forma similar, si tomamos, 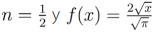 se obtiene
se obtiene
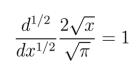
de lo cual se concluye que
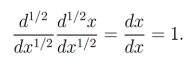
En 1822, Fourier fue el siguiente en dar una definición de derivada de orden arbitrario. Sin embargo, no se le dio utilidad a esta definición de derivada fraccionaria. El primer uso de derivadas de orden fraccionario fue dado en 1823 por Abel [17, 18], en el cual aplicó cálculo fraccionario para solucionar la ecuación integral que surge de la formulación del problema de la tautócrona. Posteriormente, en 1832 Liouville publicó tres memorias sobre el tema [19] junto con algunos trabajos de investigación. En dichos trabajos, Liouville definió a las derivadas fraccionarias con el uso de series infinitas; no obstante, las derivadas definidas mediante series infinitas estaban limitadas al intervalo de convergencia de la serie. Finalmente, mediante el uso de integrales, Liouville llegó a construir una mejor definición de derivada fraccionaria, que incluso le permitió tomar potencias negativas [17, 19].
En 1869 Sonin trabajó inicialmente en la definición de Riemann-Lioville, en un escrito llamado “En la diferenciación con índice arbitrario”, empezando con la fórmula integral de Cauchy. Letnikov escribió cuatro escritos referentes al tema los cuales tituló “Una explicación de los principales conceptos de la teoría de diferenciación de índices arbitrarios” donde dio una extensión de los escritos de Sonin. Sin embargo, no fue si no hasta 1884, que el matemático francés Laurent publicó sus escritos de la teoría de generalización de operadores partiendo del análisis complejo, dando así las bases para el calculo fraccionario [20], y referencias en el mismo.
PRELIMINARES
En esta sección se introducirán los objetos necesarios y se desarrollará una notación para el desarrollo del trabajo.
Existen funciones que juegan un papel importante en el desarrollo y entendimiento del cálculo fraccionario, a saber, la función Gamma y la de Mitagge-Leffler, las cuales juegan un papel importante al momento de buscar soluciones explícitas de ecuaciones diferenciales parciales fraccionarias. Por ende, en las siguientes subsecciones se definirán y mencionarán algunas propiedades relevantes de estas funciones.
Función Gamma
La función Gamma aparece en problemas relacionados con la normalización de funciones de onda de Coulomb o en el cálculo de probabilidades en mecánica estadística [2] y juega un rol importante en el cálculo fraccionario. La función Gamma está definida como
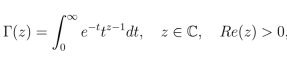
donde Re(z) denota la parte real de un numero complejo : z=a+bi, es decir Re(z)=a. La restriccion Re(z)>0 es una condición necesaria para garantizar la convergencia de la integral. La función Gamma puede ser interpretada como la generalización de un factorial, ya que ésta permite calcular factoriales de números no enteros debido a que cumple la siguiente relación:
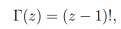
por lo cual Γ(z) también satisface la siguiente ecuación funcional [21]:
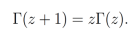
Dada la relación que guarda la función Gamma con los factoriales, se puede generalizar la ecuación (1) obtenida por Lacroix de la siguiente manera
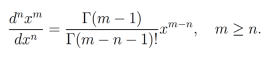
Para mas detalles sobre la funcion Gamma se recomienda ver [2].
Función de Mitagge-Leffler
Una de las funciones mas importante en este trabajo es la función de Mittagge-Leffler, ya que a pesar de no ser mencionada en las tablas de la transformada de Laplace, la función de Mitagge-Leffler surge en el cálculo de la transformada inversa de Laplace de funciones de tipo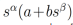 , donde s es el parámetro de la transformada de Laplace y a, b son constantes reales [22]. Por otro lado, la función de Mittage-Leffler también aparece en la solución de algunos problemas de valores de frontera que involucran ecuaciones integrodiferenciales de tipo Volterra con parámetro fraccionario[22, 23]. Está definida sobre todo el plano complejo como
, donde s es el parámetro de la transformada de Laplace y a, b son constantes reales [22]. Por otro lado, la función de Mittage-Leffler también aparece en la solución de algunos problemas de valores de frontera que involucran ecuaciones integrodiferenciales de tipo Volterra con parámetro fraccionario[22, 23]. Está definida sobre todo el plano complejo como
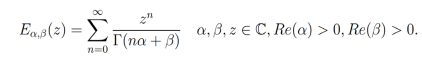 (2)
(2)En base a la ecuación (2) se puede expresar una gran variedad de funciones, por ejemplo:
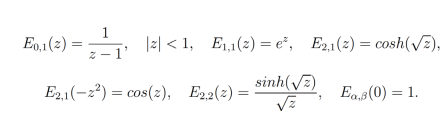
La función de Mittage-Leffler suele ser vista como una generalización de la función exponencial, por lo cual muchas de la soluciones de ecuaciones diferenciales fraccionarias son expresadas en términos de la función de Mittage-Leffler, al igual que las soluciones de ecuaciones diferenciales ordinarias son expresadas en función de senos y cosenos [17].
Cálculo fraccionario en R
A lo largo de la historia han existido varias definiciones para la derivada fraccionaria como lo son la derivada de Riemann-Liouville, Hadamard, Erdélyi-Kober, Caputo, Caputo- Fabrizio, Marchaud, por mencionar algunas [23, 24]. Sin embargo, para este trabajo únicamente nos vamos a enfocar en la definición de Riemann-Liouville, motivados por las aplicaciones en diversas áreas como nano electrónica, física y biología [25-33].
Definición 1 (Integral Fraccionaria Izquierda de Riemann-Liouville). Sea 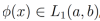 , entonces la integral fraccionaria izquierda de Riemman-Liouville
, entonces la integral fraccionaria izquierda de Riemman-Liouville 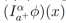 , de orden α>0 está definida como
, de orden α>0 está definida como
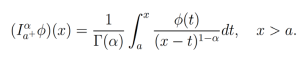 (3)
(3)
La cual suele ser denotada como 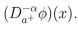
Definición 2 (Derivada Fraccionaria Izquierda de Riemann-Liouville). Sea 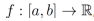 , entonces la derivada fraccionaria izquierda de Riemman-Liouville
, entonces la derivada fraccionaria izquierda de Riemman-Liouville 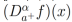 de orden α > 0 está definida como
de orden α > 0 está definida como
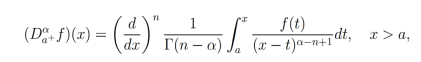
donde 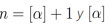 es la parte entera de α.
es la parte entera de α.
Por lo cual, tomando en cuenta la integral fraccionaria de Riemann-Liouville se tiene que las derivadas fraccionarias derecha e izquierda de Riemann-Liouville pueden ser reescritas como 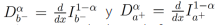 respectivamente. Notemos que, cuando 0<α<1 , entonces la derivada fraccionaria izquierda de Riemann-Liouville esta dada por la siguiente identidad:
respectivamente. Notemos que, cuando 0<α<1 , entonces la derivada fraccionaria izquierda de Riemann-Liouville esta dada por la siguiente identidad:
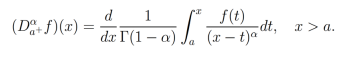 (4)
(4)De tal forma que cuando 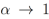 , la derivada fraccionaria
, la derivada fraccionaria 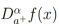 se aproxima a la derivada clásica
se aproxima a la derivada clásica  .En este trabajo analizaremos ecuaciones diferenciales con derivadas fraccionarias cuyo límite cuando
.En este trabajo analizaremos ecuaciones diferenciales con derivadas fraccionarias cuyo límite cuando 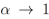 , son derivadas clásicas de orden dos. Por lo cual, sin pérdida de generalidad utilizaremos la ecuación (4) para todos los cálculos posteriores. Para ilustrar cómo funciona la derivada fraccionaria izquierda de Riemann-Liouville vamos a considerar el siguiente ejemplo:
, son derivadas clásicas de orden dos. Por lo cual, sin pérdida de generalidad utilizaremos la ecuación (4) para todos los cálculos posteriores. Para ilustrar cómo funciona la derivada fraccionaria izquierda de Riemann-Liouville vamos a considerar el siguiente ejemplo:
Ejemplo 1.Evaluemos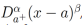 , donde β>-1 y α>0.
, donde β>-1 y α>0.
Considerando la derivada fraccionaria izquierda de Riemann-Liouville enunciada en la Definición 2, en particular considerando la ecuación (4) se tiene:
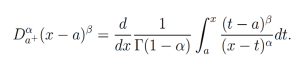
Mediante el cambio de variable z=t-a, tenemos que dz=dt, por lo que
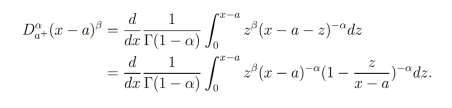
Realizando otro cambio de variable 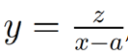 , tenemos que (x-a)dy = dt, por lo tanto
, tenemos que (x-a)dy = dt, por lo tanto
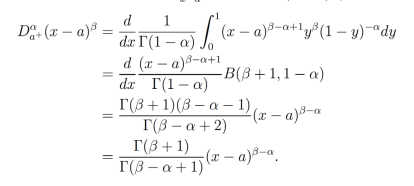
Finalmente, concluimos que
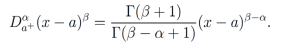 (5)
(5)Notemos que, si en la ecuación (5) tomamos β=0 , entonces (x-a)β = (x-a)0 =1, yas la derivada fraccionaria de una constante k de orden α es
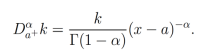
Como se puede observar, tanto la definicion de derivada como la definición integral fraccionaria incluyen integrales. Estas integrales pueden llegar a diverger, por lo que es importante considerar el espacio de funciones sobre el cual deseamos trabajar. En este artículo vamos a denotar como 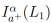 a la clase de funciones f representadas por la ecuación (3) de función integrable, es decir
a la clase de funciones f representadas por la ecuación (3) de función integrable, es decir 
Teorema 1.Sea α > 0. Entonces ,si y solo si 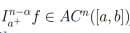 ,
, 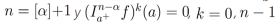 . Ver la prueba en [23].
. Ver la prueba en [23].
Observación 1. ACn[a,b] denota la clase de funciones f, tal que f es n-1 veces diferenciable en [a,b] y f(n-1) es absolutamente continua en [a,b].
Cabe mencionar que las funciones pertenecientes a 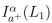 enfatizan que la representación de una función f mediante una integral fraccionaria de orden α y la existencia de la derivada fraccionaria de orden α de f son dos cosas distintas [23]. Por otro lado, la teoría de Lebesgue nos permite integrar por partes sólo si las funciones son absolutamente continuas. Debido a esto, es natural encontrar que la suposición de integrabilidad y existencia en casi todo lado de las derivadas fraccionarias
enfatizan que la representación de una función f mediante una integral fraccionaria de orden α y la existencia de la derivada fraccionaria de orden α de f son dos cosas distintas [23]. Por otro lado, la teoría de Lebesgue nos permite integrar por partes sólo si las funciones son absolutamente continuas. Debido a esto, es natural encontrar que la suposición de integrabilidad y existencia en casi todo lado de las derivadas fraccionarias 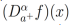 no es suficiente para nuestro estudio, ya que la integrabilidad y existencia en casi todo lado de las derivadas fraccionarias no garantiza la representación de f mediante integrales fraccionarias. Por estas razones, para estudiar la reciprocidad entre la derivada y la integral fraccionaria es necesario imponer una condición más fuerte sobre f, con lo que se da paso a la siguiente definición:
no es suficiente para nuestro estudio, ya que la integrabilidad y existencia en casi todo lado de las derivadas fraccionarias no garantiza la representación de f mediante integrales fraccionarias. Por estas razones, para estudiar la reciprocidad entre la derivada y la integral fraccionaria es necesario imponer una condición más fuerte sobre f, con lo que se da paso a la siguiente definición:
Definición 3.Sea α > 0. Una función 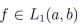 tiene una derivada integrable
tiene una derivada integrable 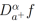 si
si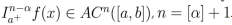 .
.
De tal forma que la relación entre la derivada y la integral fraccionaria se enuncia en el siguiente teorema:
Teorema 2.Sea α > 0. Entonces la ecuación
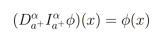
se mantiene para cualquier función integrable Φ(x). Sin embargo,
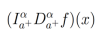
sólo se satisface si
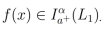
Si asumimos que 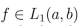 tiene una derivada integrable
tiene una derivada integrable 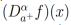 respecto a la definición 3, entonces la identidad (6) no se cumple; de hecho, es remplazada por el siguiente resultado:
respecto a la definición 3, entonces la identidad (6) no se cumple; de hecho, es remplazada por el siguiente resultado:
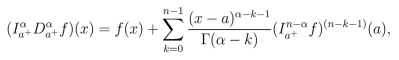
con n = [α]+1. Ver la prueba en [23].
Proposición 1. (Propiedad de semi-grupo de la derivada fraccionaria). Sea α>0 y β>0 tal que n-1<α ≤ n y m-1<β≤m y α+β≤1 y sea 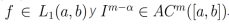 . Entonces, se cumple la siguiente relación:
. Entonces, se cumple la siguiente relación:
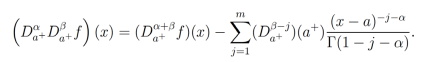
Ver prueba en [23, 34].
En particular la propiedad del semigrupo es 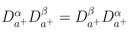 siempre y cuando
siempre y cuando
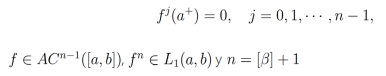
Existe la definición de la derivada aproximándose a la derecha, ver [23]. No obstante,nosotros sólo nos enfocaremos en la izquierda.
Transformada de Laplace
La idea principal de la transformada de Laplace es convertir una ecuación que involucra derivadas e integrales en una expresión algebraica [35]. Esto permite resolver ecuaciones diferenciales de una forma más sencilla, en especial si se cuenta con condiciones iniciales [17].
Para ilustrar la relación que guarda la transformada de Laplace con funciones importantes del cálculo fraccionario, como son la función Gamma y la función de Mittage-Leffler, consideremos las siguientes proposiciones:
Proposición 2. Sea 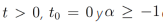 . Entonces la transformada de Laplace de
. Entonces la transformada de Laplace de 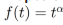 existe, y está dada por la siguiente ecuación:
existe, y está dada por la siguiente ecuación:
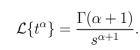
Demostración. Sea 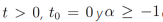 entonces la transformada de Laplace de
entonces la transformada de Laplace de 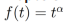 está definida de la siguiente forma
está definida de la siguiente forma
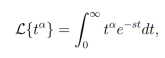 (7)
(7)utilizando el cambio de variable  , por lo cual (7) se reescribe de la siguiente forma
, por lo cual (7) se reescribe de la siguiente forma
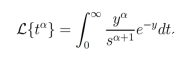
Sacando 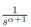 de la integral y dado que α≥-1, se obtiene una función Gamma, con z=α+1 de tal forma que
de la integral y dado que α≥-1, se obtiene una función Gamma, con z=α+1 de tal forma que
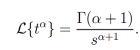
Proposición 3. Sea 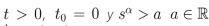 , entonces la transformada de Laplace de
, entonces la transformada de Laplace de 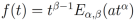 existe, y esta dada por la siguiente ecuación
existe, y esta dada por la siguiente ecuación
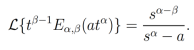 (8)
(8)
Demostración. Sea 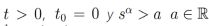 , entonces la transformada de Laplace de
, entonces la transformada de Laplace de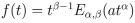 está definida de la siguiente forma
está definida de la siguiente forma
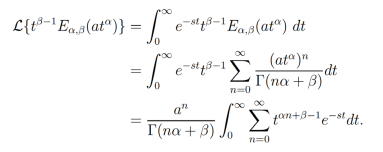
Dada la convergencia de la integral y de la serie podemos intercambiar estas [21]:
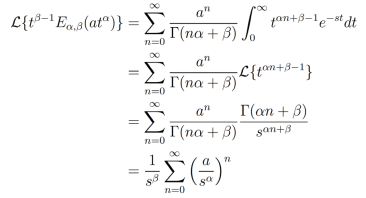 (9)
(9)Por último, dado que sα > a, la serie en la ecuación (9) converge, por lo cual
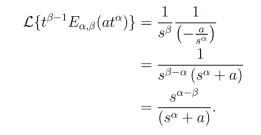
Transformada de Laplace de la Derivada Fraccionaria
A partir de esta subsección vamos a denotar a las funciones evaluadas en 0, es decir f(0), como 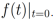 . Esto permite involucrar condiciones iniciales al problema. Sin embargo, las condiciones iniciales no son discutidas en este artículo.
. Esto permite involucrar condiciones iniciales al problema. Sin embargo, las condiciones iniciales no son discutidas en este artículo.
Proposición 4. Sea f una función Laplace transformable. Entonces la transformada de Laplace de la derivada fraccionaria de orden α de Riemann-Lioville centrada en a+=0 está dada por
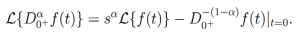 (10)
(10)Demostración. consideremos la derivada fraccionaria de Riemann-Liouville
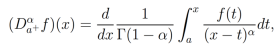
la cual puede ser reescrita como
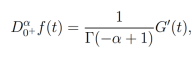
donde 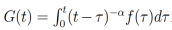 . Tomando la transformada de laplace de (11) obtenemos
. Tomando la transformada de laplace de (11) obtenemos
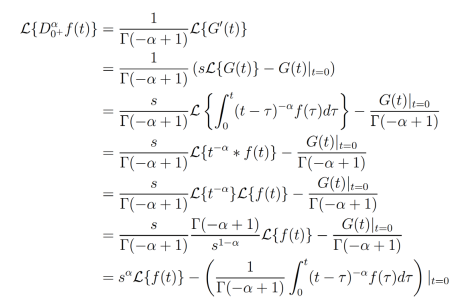
Cambiando α por -α+1 y usando la ecuación (3) obtenemos que.
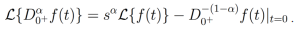
Proposición 5. Sea η(x) una función Laplace transformable. Entonces la transformada de Laplace de la derivada fraccionaria de orden 2α de Riemann-Liouville centrada en a+=0 es
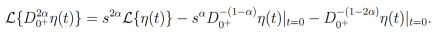
Demostración. Sea η(x) una función Laplace transformable. Entonces por la Proposición 4 se obtiene
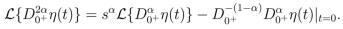
Simplificando,
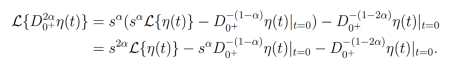
Procediendo de igual forma que en la demostración de la Proposición 4 y utilizando las propiedades de convolución, se pueden mostrar las siguientes relaciones:
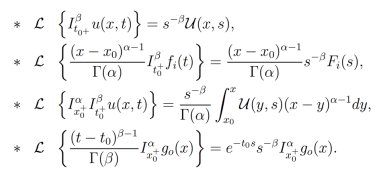
Donde 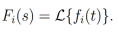
Espacio de Zemanian
Se conoce al espacio de Zemanian como el espacio en el cual viven las transformadas de Laplace. Por lo cual, para obtener la transformada inversa de Laplace se necesita tomar en cuenta su forma generalizada en dicho espacio. Por lo que tenemos las siguientes relaciones presentadas en el trabajo de Ferreira y Vieira [14]
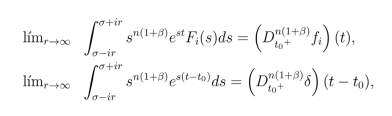
donde 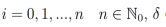 es la función delta de Dirac, y su convergencia es en
es la función delta de Dirac, y su convergencia es en 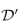
Ecuaciones integrales
Las ecuaciones integrales son aquellas que relacionan una función incógnita con una integral, de tal manera que la función incógnita se encuentre bajo el signo integral. Análogamente a las ecuaciones diferenciales, las ecuaciones integrales pueden ser de orden lineal y no lineal. En el caso de ecuaciones integrales lineales podemos encontrar las de tipo Fredholm y las de tipo Volterra [15].
1. Ecuaciones de tipo Fredholm: Son aquellas ecuaciones integrales con límites de integración fijos. Éstas pueden ser clasificadas en dos grupos:
-
Primera especie: La función incógnita sólo está bajo el signo integral:
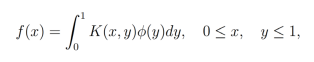
donde Φ(x) es la función incógnita, K(x,y), f(x) son funciones conocidas y K(x,y) es continua en el cuadrado 0≤x, y≤1 [36].
-
Segunda especie: La función incógnita se encuentra bajo el signo integral y fuera de él.
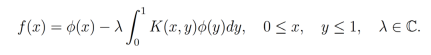
Si f(x)=0, se conoce como ecuación homogénea, mientras que si f(x)≠0 se conoce como ecuación completa o no homogénea.
2. Ecuaciones de tipo Volterra: Son un caso particular de las ecuaciones de tipo Fredholm en el cual se satisface que K(x,y) > 0 si y > x. Por lo cual, de la misma forma que con las ecuaciones de tipo Fredholm, podemos clasificar las ecuaciones de tipo Volterra en dos grupos
-
Primera especie: La función incógnita sólo está bajo el signo integral.
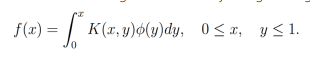
-
Segunda especie: La función incógnita aparece tanto bajo el signo integral como fuera de él.
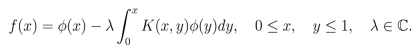
Observación 2. A la función K(x. y] se le conoce como el Kernel o núcleo de la ecuación.
A pesar de la complejidad de las ecuaciones integrales, el método de descomposición de Adomian [15, 37] es efectivo al momento de buscar una solución de ecuaciones integrales. Dicho método consiste en descomponer la función incógnita en una serie infinita de la siguiente forma:
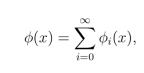
donde 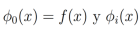 son determinados a partir de la siguiente fórmula recursiva
son determinados a partir de la siguiente fórmula recursiva
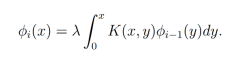
Utilizando el
método de Adomian se puede encontrar una solución
para ecuaciones integrales de Volterra de segundo tipo. En
particular, dado un kernel 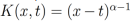 se puede enunciar el siguiente teorema.
se puede enunciar el siguiente teorema.
Teorema 3. [15] Sea 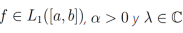 . Entonces la ecuación integral
. Entonces la ecuación integral
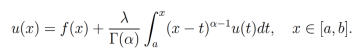
Tiene una única solución dada por
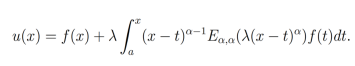
CÁLCULO FRACCIONARIO PARA ECUACIONES DIFERENCIALES
En este trabajo se estudian dos métodos distintos para encontrar soluciones explícitas de ecuaciones diferenciales parciales fraccionarias, las cuales fueron propuestas por grupos de trabajo interdisciplinario. Para esto, se considera el siguiente conjunto de tres ecuaciones diferenciales parciales, que son parte central de los resultados obtenidos por dichos grupos
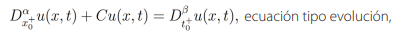 (13)
(13)
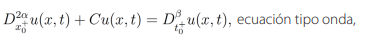 (14)
(14)
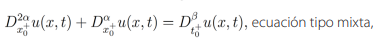 (15)
(15)de tal manera que cuando  , las ecuaciones (13), (14), (15) se comportan de forma clásica como se muestra a continuación:
, las ecuaciones (13), (14), (15) se comportan de forma clásica como se muestra a continuación:
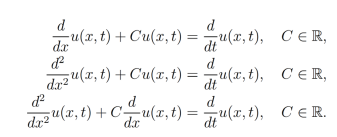
Solución por producto de funciones
La metodología usada en esta sección consiste en reducir una ecuación diferencial parcial fraccionaria a dos ecuaciones diferenciales ordinarias fraccionarias que puedan ser resueltas mediante la transformada de Laplace, de tal forma que la solución del problema inicial sea el producto de éstas. Para esto, vamos a considerar la derivada de Riemann-Liouville de orden 2α centrada en a+=0, esto es,. La construcción de las soluciones por esta metodología puede ser resumidas en los siguientes pasos:
Paso 1: Proponer una solución de tipo producto de funciones u(x,t) = u(x)u(t) tal que u(x), u(t) ∈ C[0, b], y separar la parte espacial de la temporal.
Paso 2: Resolver las ecuaciones diferenciales fraccionarias homogéneas mediante la transformada de Laplace.
Paso 3 : Expresar la solución del problema original como un producto de funciones.
Para ilustrar dicho método, consideremos la siguiente ecuación diferencial parcial fraccionaria:
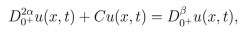 (16)
(16)Comencemosconelpaso 1.Consideremos
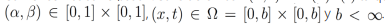 . Reemplazando u(x,t) en la ecuación (16) y realizando algunos cálculos directos se tiene que
. Reemplazando u(x,t) en la ecuación (16) y realizando algunos cálculos directos se tiene que
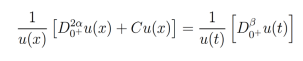 (17)
(17)Para que los dos lados de la ecuación (17) sean iguales, estos deben ser igual a una constante, por lo cual se tiene que
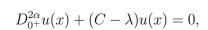 (18)
(18)
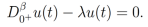 (19)
(19)Continuando con el paso 2, buscamos soluciones para las ecuaciones (18) y (19) con λ ∈ R. Estas soluciones pueden ser obtenidas mediante las siguientes proposiciones
Proposición 6. Sea 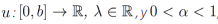 , entonces la ecuación diferencial fraccionaria ordinaria
, entonces la ecuación diferencial fraccionaria ordinaria
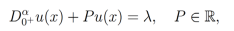 (20)
(20)tiene como solución
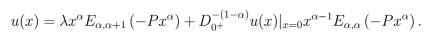 (21)
(21)
Demostración. Sea 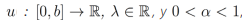 , por lo cual tomando la transformada de Laplace de (20) se tiene
, por lo cual tomando la transformada de Laplace de (20) se tiene
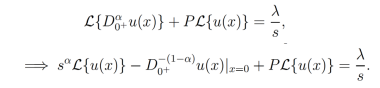 (22)
(22)Ordenando la ecuación (22) y mediante algunos cálculos directos se tiene la siguiente solución
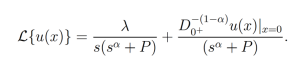 (23)
(23)Finalmente, con ayuda de la ecuación (8) con β=α+1, β=α para el primer y segundo término, se toma la transformada inversa de Laplace de la ecuación (23). Así obtenemos
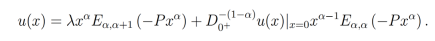
Proposición 7. Sea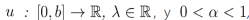 , entonces la ecuación diferecia fraccionariaordinaria
, entonces la ecuación diferecia fraccionariaordinaria
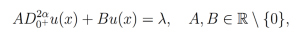 (24)
(24)tiene como solución
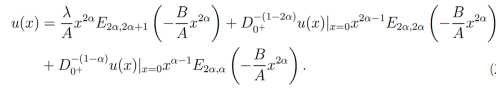 (25)
(25)
Demostración. Sea 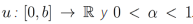 . Entonces la ecuación (24) puede ser reescrita como
. Entonces la ecuación (24) puede ser reescrita como
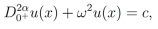 (26)
(26)donde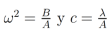 . Tomando la transformada de laplace de (26):
. Tomando la transformada de laplace de (26):
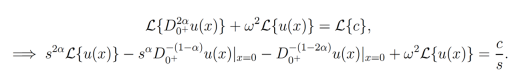
La cual puede ser escrita de forma reducida como
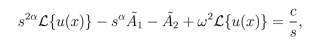 (27)
(27)donde 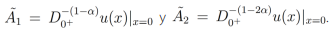 . Ordenando la ecuación (27) y mediante algunos cálculos directos se obtiene que
. Ordenando la ecuación (27) y mediante algunos cálculos directos se obtiene que
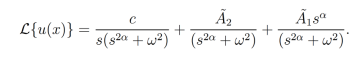 (28)
(28)Finalmente, con ayuda de la ecuación (8) con β=2α+1,β=2α ,β=α para el primer, segundo y tercer término respectivamente, se toma la transformada de Laplace del lado derecho de la ecuación (28). Así obtenemos
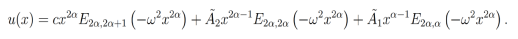
O equivalentemente:
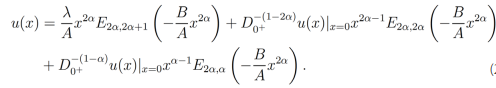
Para concluir con el paso 3, usando las Proposiciones 6 con λ = 0 y P = λ y 7 con A = 1, B = (C-λ) y λ = 0 obtenemos que la solución de la ecuación diferencial parcial fraccionaria (16) está dada por
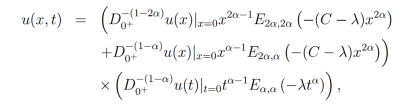
De tal forma que se puede enunciar el siguiente teorema:
Teorema4.Sea 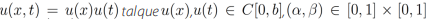
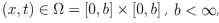 , entonces la ecuación diferencial parcial fraccionaria
, entonces la ecuación diferencial parcial fraccionaria
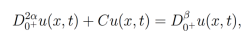
tiene como solución
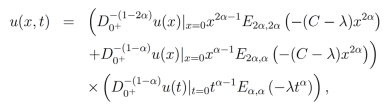
Donde 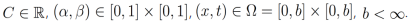
De manera análoga, usando apropiadamente las Proposiciones 6 y 7, se demuestra el siguiente teorema:
Teorema 5. Sea 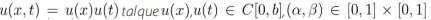
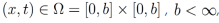 , entonces la ecuación diferencial parcial fraccionaria
, entonces la ecuación diferencial parcial fraccionaria
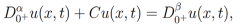
tiene como solución
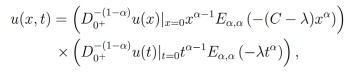
donde 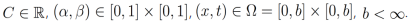
Solución por integración directa
La metodología usada en esta sección consiste en integrar directamente la ecuación diferencial parcial fraccionaria, de tal forma que, tomando en cuenta la relación entre la integral y la derivada fraccionaria, se encuentra una ecuación cuyos términos son Laplace transformables. Para esto, vamos a considerar (α,β) ∈ [0,1]x[0,1], 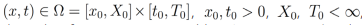 tal que u(x,t) admite derivadas fraccionarias integrables. La construcción de las soluciones por esta metodología puede ser resumida en los siguientes pasos:
tal que u(x,t) admite derivadas fraccionarias integrables. La construcción de las soluciones por esta metodología puede ser resumida en los siguientes pasos:
Paso 1: Se integra directamente y se toma en cuenta la relación entre la integral y la derivada fraccionaria (Teorema 2).
Paso 2: Se aplica la transformada de Laplace para llegar a una ecuación integral de tipo Volterra de segunda especie.
Paso 3: Se resuelve la ecuación integral y se simplifica.
Paso 4: Se toma la transformada inversa de Laplace.
Para ilustrar dicho método consideremos la siguiente ecuación diferencial parcial fraccionaria:
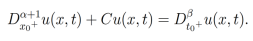
Comencemos con el paso 1. Consideremos la ecuación (29), donde C∈R. 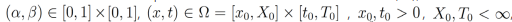 y u(x,t) admite derivadas fraccionarias sumables
y u(x,t) admite derivadas fraccionarias sumables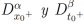 . Aplicando el operador integral
. Aplicando el operador integral 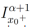 . a los dos lados de la ecuación (29) y, tomando en cuenta la relación entre la integral y la derivada fraccionaria enunciada en el Teorema 2, se tiene que
. a los dos lados de la ecuación (29) y, tomando en cuenta la relación entre la integral y la derivada fraccionaria enunciada en el Teorema 2, se tiene que
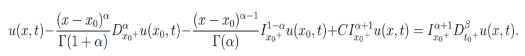
De forma similar, aplicando el operador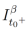 . a los dos lados a la ecuación anterior y utilizando el teorema de Fubini, se toma en cuenta la relación entre la integral y derivada fraccionaria enunciada en el Teorema 2 de tal forma que se obtiene
. a los dos lados a la ecuación anterior y utilizando el teorema de Fubini, se toma en cuenta la relación entre la integral y derivada fraccionaria enunciada en el Teorema 2 de tal forma que se obtiene
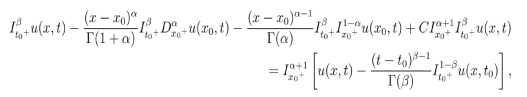
la cual es equivalente a
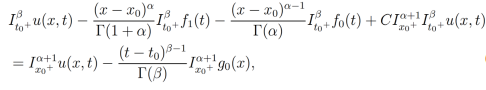 (30)
(30)donde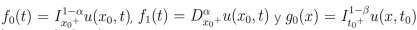 , que son las condiciones de Cauchy.
, que son las condiciones de Cauchy.
Continuando con el paso 2, se toma la transformada de Laplace respecto a . de la ecuación (30) y utilizando sus propiedades de convolución se obtiene que
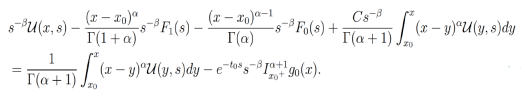 (31)
(31)Multiplicando la ecuación (31) por sβ. reorganizando sus términos obtenemos la siguiente ecuación de tipo Volterra:
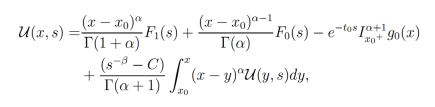 (32)
(32)Procediendo con el paso 3, se toma en cuenta que la ecuación (32) en virtud del Teorema 3, tiene como única solución
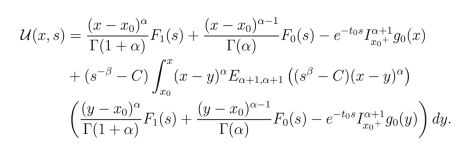 (33)
(33)Dada la convergencia de las integrales y las series en la ecuación (33) podemos intercambiar éstas y reescribirla de la siguiente forma:
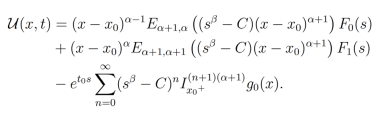
Para concluir con el paso 4, se requiere cancelar la transformada de Laplace, por consiguiente tomamos en cuenta su forma distribucional y con ayuda del teorema multinomial y mediante algunos cálculos directos, podemos dejar la solución expresada en términos de la función de Mittage-Leffler
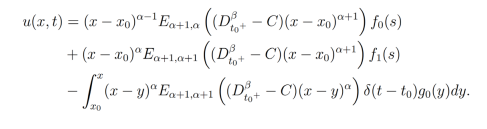
Donde 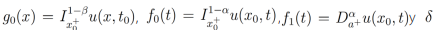 es la función delta de Dirac.
es la función delta de Dirac.
De tal forma quese puede enunciar el siguiente teorema
Teorema 6.Sea 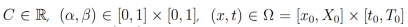
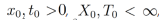 , tal que u(x,t) admite derivadas fraccionarias integrables
, tal que u(x,t) admite derivadas fraccionarias integrables 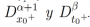 . Entonces la ecuación diferencial parcial fraccionaria
. Entonces la ecuación diferencial parcial fraccionaria
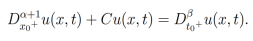
tiene como solución
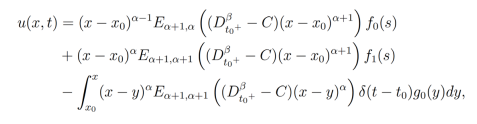
donde 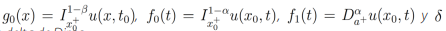 es la función delta de Dirac.
es la función delta de Dirac.
Análogamentese puede demostrar elsiguiente teorema
Teorema 7. Sea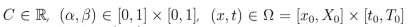
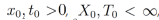 tal que u(x,t) admite derivadas fraccionarias integrables
tal que u(x,t) admite derivadas fraccionarias integrables 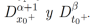 . Entonces la ecuación diferencial parcial fraccionaria
. Entonces la ecuación diferencial parcial fraccionaria
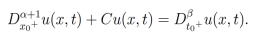
tiene como solución
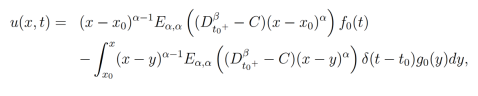
donde 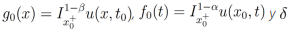 es la función delta de Dirac.
es la función delta de Dirac.
CONCLUSIONES
Si bien el uso de la transformada de Laplace es un gran método para resolver ecuaciones diferenciales, éste puede involucrar cálculos extremadamente difíciles. A pesar de que una gran cantidad de transformadas inversas de Laplace de funciones tipo sα(a+bsβ) pueden ser expresadas mediante la función de Mittage-Leffler, el cálculo de transformadas inversas de Laplace está limitado por el orden de α, ya que al ser éste variable, es difícil encontrar una factorización adecuada mediante fracciones parciales. Dicho esto, se puede observar que proponiendo una solución de tipo producto de funciones podemos llegar a encontrar de una forma más sencilla la solución de una ecuación diferencial parcial fraccionaria de segundo orden, reduciéndola a dos ecuaciones diferenciales ordinarias fraccionarias homogéneas. A pesar de ello, la propiedad de semi-grupo de la derivada fraccionaria de Riemann-Liouville nos dice que para derivadas de orden 2α nuestra solución solo es válida para α ∈ (1/2 , 1).
Por otro lado, se puede observar que la relación entre la integral y derivada fraccionaria puede llevarnos a encontrar ecuaciones de Volterra de segunda especie. Si bien es cierto que la importancia del orden de integración y derivación depende del espacio en donde se trabaje, el uso de funciones L1 nos permite llegar a ecuaciones de Volterra de segunda especie, asegurando así una única solución. Hay que destacar que la existencia de la ecuación de tipo Volterra depende de que todas las derivadas respecto a la misma variable tengan el mismo orden, es decir no se puede tener derivadas de orden 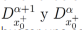 dentro de una misma ecuación diferencial parcial fraccionaria si se desea buscar una solución por el método de integración directa. La ventaja de usar el método de integración directa es que permite extenderlo a múltiples dimensiones de una manera mucho más simple que el método de la solución por producto.
dentro de una misma ecuación diferencial parcial fraccionaria si se desea buscar una solución por el método de integración directa. La ventaja de usar el método de integración directa es que permite extenderlo a múltiples dimensiones de una manera mucho más simple que el método de la solución por producto.
La particularidad de estos métodos es que están limitados a coeficientes constantes por lo cual el siguiente paso a seguir sería trabajar con ecuaciones diferenciales fraccionarias, parciales y ordinarias con coeficientes variables. Para esto, se propone en un futuro definir de una manera conveniente la ley de la cadena y expandir al método de Frobenius al caso fraccionario, ya que muchas de las ecuaciones diferenciales que describen fenómenos físicos son resueltas por estos métodos. En particular, el método de Frobenius nos ayuda a resolver ecuaciones diferenciales cuya solución son funciones especiales, como los polinomios de Hermite o Laguerre [2], de tal forma que extendiendo el método de Frobenius al caso fraccionario podamos calcular funciones especiales de orden no entero.
Finalmente, este trabajo se limitó a buscar soluciones generales a las ecuaciones diferenciales parciales fraccionarias propuestas, por lo que no se profundizó sobre problemas de valores iniciales y problemas de valores de frontera específicos sobre los resultados obtenidos. Sin embargo, las soluciones obtenidas consideran las condiciones iniciales y condiciones de frontera como constantes, de tal forma que los grupos de trabajo interdisciplinario puedan usarlas con mayor libertad.
CONTRIBUCIONES DE LOS AUTORES
Ambos autores contribuyeron en partes iguales en todas las etapas de elaboración del articulo, desde el proceso creativo pasando por los cálculo, redacción, corrección hasta llegar a la edición final.
REFERENCIAS
[1] Ansorge, R. & Sonar, T. (2009). Mathematical models of fluid dynamics. Wiley Online Library.
[2] Arfken, G. & Weber, H. (1999). Mathematical methods for physicists. American Association of Physics Teachers.
[3] Spiegelhalter, D., Best, N. & Carlin, B. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64 (4), 583-639.
[4] Edelman, M. (2013). Fractional Dynamical Systems. doi:10 . 1109 / ICFDA . 2014 . 6967376. eprint: arXiv:1401.0048
[5] Sumelka, W., Zaera, R. & Fernández-Sáez, J. (2015). A theoretical analysis of the free axial vibration of non- local rods with fractional continuum mechanics. Meccanica, 50 (9), 2309-2323.
[6] Carpinteri, A., Cornetti, P. & Sapora, A. (2014). Nonlocal elasticity: an approach based on fractional calculus. Meccanica, 49 (11), 2551-2569. DOI 10.1007/s11012-014-0044-5
[7] Craiem, D., Rojo, F., Atienza, J., Guinea, G. & Armentano, R. (2008). Fractional calculus applied to model arterial viscoelasticity. Latin American applied research, 38 (2), 141-145.
[8] Applebaum, D. (2004). Lévy processes from probability to finance and quantum groups. Notices of the AMS, 51 (11), 1336-1347.
[9] Tarasova, V. & Tarasov, V. (2016). Elasticity for economic processes with memory: Fractional differential calculus approach. Fractional Differential Calculus, 6 (2), 219-232.
[10] El-Ajou, A., Odibat, Z., Momani, S. & Alawneh, A. (2010). Construction of Analytical Solutions to Fractional Differential Equations Using Homotopy Analysis Method. International Journal of Applied Mathematics, 40 (2).
[11] Haberman, R. (1983). Elementary applied partial differential equations. Prentice Hall Englewood Cliffs, NJ.
[12] O’Neil, P. V. (2011). Beginning partial differential equations. John Wiley & Sons.
[13] Zill, D. (2012). A first course in differential equations with modeling applications. Cengage Learning.
[14] Ferreira, M. & Vieira, N. (2016). Eigenfunctions and fundamental solutions of the fractional Laplace and Dirac operators: the Riemann-Liouville case. Complex Analysis and Operator Theory, 10 (5), 1081-1100.
[15] Caballero, M. (2019). Una introducción a las ecuaciones integrales lineales. Recuperado desde https://hdl. handle.net/11441/90001
[16] Calderón, M., Rosales, J., Guzmán, R., González, A. & Álvarez, J. (2015). El cálculo diferencial e integral fraccionario y sus aplicaciones. Acta universitaria, 25 (2), 20-27.
[17] Almusharrf, A. (2011). Development of fractional trigonometry and an application of fractional calculus to pharmacokinetic model.
[18] Abel, N. (1881). Solution de quelques problemes a l’aide d'intégrales définies. Oeuvres, 1, 11-27.
[19] Liouville, J. (1834). Mémoire sur le théoreme des fonctions complémentaires. Journal für die reine und angewandte Mathematik, 1834 (11), 1-19.
[20] Muñoz, J. M. S. (2011). Génesis y desarrollo del Cálculo Fraccional. Pensamiento Matemático, (1), 4.
[21] Rudin, W. (1964). Principles ofmathematical analysis. McGraw-hill New York.
[22] Haubold, H., Mathai, A. & Saxena, R. (2011). Mittag-Leffler functions and their applications. Journal of Applied Mathematics, 2011.
[23] Samko, S., Kilbas, A. & Marichev, O. (1993). Fractional integrals and derivatives. Gordon y Breach Science Publishers, Yverdon Yverdon-les-Bains, Switzerland.
[24] Almeida, R. (2017). A Caputo fractional derivative of a function with respect to another function. Communications in Nonlinear Science and Numerical Simulation, 44, 460-481.
[25] Alsaedi, A., Nieto, J. J. & Venktesh, V. (2015). Fractional electrical circuits. Advances in Mechanical Engineering, 7 (12), 1687814015618127.
[26] Baleanu, D., Golmankhaneh, A. K. & Golmankhaneh, A. K. (2009). The dual action of fractional multi time Hamilton equations. International Journal of Theoretical Physics, 48 (9), 2558-2569.
[27] Baleanu, D., Golmankhaneh, A. K., Golmankhaneh, A. K. & Nigmatullin, R. R. (2010). Newtonian law with memory. Nonlinear Dynamics, 60 (1-2), 81-86.
[28] Baleanu, D., Güven^c, Z. B. & Machado, J. T. (Eds.). (2010). New trends in nanotechnology and fractional calculus applications. doi:https://doi.org/10.1007/978-90- 481-3293-5
[29] Caputo, M. (2014). The role of memory in modeling social and economic cycles of extreme events. En F. Francesco, M. Ram & M. N. Pietro (Eds.), A Handbook of Alternative Theories of Public Economics. doi:https://doi.org/10.4337/9781781004715
[30] Caputo, M. & Cametti, C. (2008). Diffusion with memory in two cases of biological interest. Journal of theoretical biology, 254 (3), 697-703.
[31] Caputo, M., Cametti, C. & Ruggero, V. (2008). Time and spatial concentration profile inside a membrane by means of a memory formalism. Physica A: Statistical Mechanics and its Applications, 387 (8-9), 2010-2018.
[32] Caputo, M. & Fabrizio, M. (2015). Damage and fatigue described by a fractional derivative model. Journal of Computational Physics, 293, 400-408.
[33] Cesarone, F., Caputo, M. & Cametti, C. (2004). Memory formalism in the passive diffusion across a biological membrane. J. Membrane Sci, 250, 79-84.
[34] Podlubny, I. (1998). Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier.
[35] Schiff, J. (2013). The Laplace transform: theory and applications. Springer Science & Business Media.
[36] Molano Cabrera, S. A. & Lesmes Acosta, M. d. C. (2007). La alternativa de Fredholm.
[37] Ballén López, J. & León, P. (2017). Método de descomposición de Adomian (Tesis de maestría, Universidad EAFIT).