Algoritmo de autocalibración de los parámetros extrínsecos de un sistema de visión estéreo mediante optimización de colonia de hormigas
Self-calibration of extrinsic parameters of a stereoscopic vision system by using ant colony optimization
ACI Avances en Ciencias e Ingenierías
Universidad San Francisco de Quito, Ecuador
Recepción: 21 Febrero 2019
Aprobación: 09 Enero 2020
Resumen: En esta investigación se presenta un algoritmo para la autocalibración de los parámetros extrínsecos de una cámara estereoscópica mediante el uso de la infraestructura vial y un algoritmo metaheurístico, para estimar la altura y los ángulos de cabeceo, balanceo y guiñada. Este algoritmo está constituido por tres etapas; la primera es un modelo de las ecuaciones no lineales que relacionan la altura y los ángulos. La segunda etapa es la extracción de la información visual de la infraestructura vial capturada por el sistema de visión estéreo, en este caso las líneas de la carretera. Finalmente se realiza la implementación de una metaheurística basada en el algoritmo de optimización colonia de hormigas para solucionar el modelo matemático mundo-cámara. Los resultados experimentales muestran la correcta estimación de los cuatro parámetros, obteniéndose un error global del 8% y del 9% en escenarios de laboratorio y reales de carretera, respectivamente.
Palabras clave: Autocalibración, parámetros extrínsecos, optimización, colonia de hormigas, visión estereoscópica.
Abstract: This research presents an algorithm for self-calibration of the extrinsic parameters of a stereoscopic vision system by using both road infrastructure and a metaheuristic algorithm, to estimate the pitch, roll and yaw angles, and the height. This algorithm is constituted by three stages: The first one is a non-linear equation of the height and angles. The second one is the extraction of visual information from the road infrastructure captured by the stereo vision system, in this case, the lines of the road. Finally, the implementation of a metaheuristic based on the ant colony optimization algorithm is carried out to solve the mathematical model which represents the world camera. Experimental results show the correct estimation of the four parameters, obtaining anoverall error of 8% and 9% in scenarios of laboratory and real road, respectively.
Keywords: Self-calibration, extrinsic parameters, optimization, ant colony, stereoscopic vision.
INTRODUCCIÓN
En los últimos años, una tendencia mundial es el desarrollo de tecnología destinada al campo de los vehículos inteligentes y autónomos [1], [2], y a los sistemas avanzados de asistencia a la conducción [2-6], para aumentar el confort, mejorar la seguridad vehicular, etc.
Tanto es así que en este trabajo se establece el punto inicial para el desarrollo de sistemas con características de navegación autónoma, ya que se busca establecer una correspondencia entre la información visual capturada por un sistema estereoscópico y la escena tridimensional formada por la infraestructura vial, la cual permitirá calibrar los parámetros extrínsecos del sistema de visión estereoscópico de manera automática, sin necesidad de la intervención humana.
La autocalibración de extrínsecos se entiende como la estimación de la altura (h) y los ángulos de cabeceo (α), guiñada (β) y balanceo (γ). Estos ángulos permiten describir la orientación del sistema estereoscópico en tres dimensiones. Todo esto en el contexto de relacionar los sistemas de referencia del sistema estereoscópico y el mundo. La Fig. 1(a), ilustra la relación entre los mundos de referencia de los sistemas de visión estereoscópico y real, a la vez, la Fig. 1(b) muestra como el sistema de visión estereoscópico, montado sobre el parabrisas de un vehículo, utiliza la infraestructura vial de las líneas de la carretera.
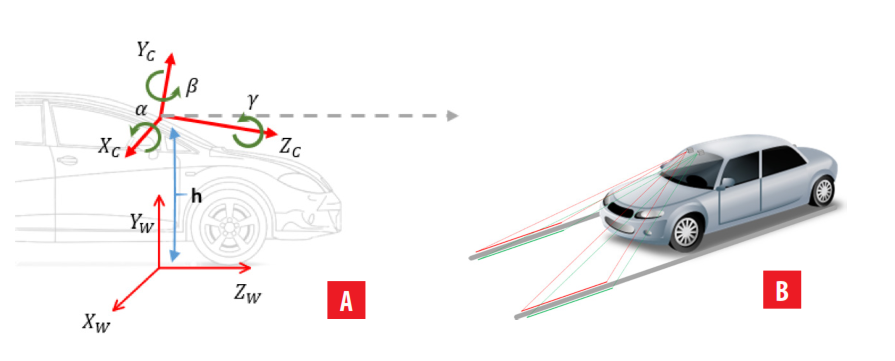
FIGURA 1.
Descripción general del algoritmo de autocalibración del sistema estereoscópico, (A) sistemas de coordenadas del mundo (W) y de la cámara (C), separados una altura (h), (B) ilustración del sistema estereoscópico sobre el vehículo y al frente las líneas de la carretera.
Este método, de autocalibración de extrínsecos, se basa en una extensión al trabajo de Collado et al [5] y el uso del algoritmo de optimización de colonia de hormigas (ACO, Sp Ant Colony Optimization) [7-9] para optimizar una función no lineal que relaciona el mundo de las cámaras y el mundo real.
Este paso es importante para el desarrollo de sistemas avanzados de asistencia a la conducción, vehículos inteligentes y vehículos autónomos, porque cada vez que el sistema de visión cambia de posición se necesita de un proceso previo de calibración, para así tener referencia del mundo en el cual se moverán.
Este documento está organizado de la siguiente manera. La primera sección corresponde a la motivación que ha generado esta investigación. La siguiente sección presenta los trabajos previos en la autocalibración de los parámetros extrínsecos en sistemas de visión estereoscópico. A continuación, el apartado tres describe un nuevo algoritmo para solucionar el modelo de Collado et al. [5] extendido al caso de tres ángulos. Seguidamente, la siguiente sección exhibe los resultados experimentales. Finalmente, la última parte está dedicada a las conclusiones y los trabajos futuros.
MATERIALES Y MÉTODOS
Estado del Arte
La calibración se define como el proceso mediante el cual se calculan los parámetros intrínsecos y extrínsecos del sistema de visión estereoscópica. La calibración de intrínsecos consiste en determinar las condiciones de formación de la imagen, es decir, determinar la relación entre coordenadas imagen y las direcciones de vista en el espacio. La calibración de extrínsecos consiste en determinar la posición y orientación del sistema estereoscópico respecto a un sistema de referencia preestablecido. [5], [10-14]
Broggi et al. [3] ha presentado un método de calibración usando marcas viales cuya posición es conocida, a partir de la cual permite determinar la posición y orientación de la cámara respecto al vehículo. Esta autocalibración se realiza en una etapa de calibración supervisada usando un patrón pintado frente al vehículo. Dang et al. [15] ha presentado un sistema de autocalibración de extrínsecos considerando inexactitudes mecánicas en la configuración del sistema de visión y usando de filtro Kalman extendido para obtener los parámetros en todo tiempo. Collado et al [5] ha desarrollado la autocalibración usando un algoritmo genético para la estimación de parámetros, bajo las hipótesis de mundo plano sobre infraestructura vial. Wang et al. [16] han estimado los ángulos y la altura usando el algoritmo de RANSAC [17] para eliminar valores atípicos. Este trabajo es aplicado a sistemas de navegación en ambientes de agricultura. Musleh et al. [18] han utilizado la imagen de disparidad, la transformada de Hough y algoritmo de RANSAC [17] para obtener la estimación geométrica del ambiente y así estimar la calibración extrínseca. Otra propuesta es la de Spangenberg et al. [19] que han basado su esquema en el uso de las técnicas Monte-Carlo para minimizar los costos de emparejamiento de los puntos coincidentes en las imágenes del sistema de visión para recalcular los parámetros extrínsecos periódicamente. Por otra parte, de Paul et al [20] ha realizado una aplicación de la calibración automática de cámaras sobre la marcha y aplicaciones de realidad aumentada para sistemas de asistencia al conductor e inspección de carreteras, donde la autocalibración no requiere conocimiento de parámetros o patrones de calibración a priori. La distancia entre las líneas viales se detecta basándose en la velocidad del vehículo.
Sistema de percepción y procesamiento
El sistema total (hardware y software) está compuesto por: dos cámaras, una pantalla de visualización, una tarjeta de procesamiento, y el programa de computador desarrollado en este trabajo.
Este prototipo es de fácil instalación en cualquier tipo de plataforma móvil. En particular, en un vehículo, debido a su reducido tamaño, por lo que no interfiere en las labores de conducción y no obstaculiza la visibilidad. En la Fig. 2 se observa en detalle.
DESCRIPCIÓN DEL SISTEMA
El esquema del sistema propuesto se muestra en la Fig. 3, el mismo que está compuesto de cuatro etapas.

FIGURA 2.
Prototipo para la calibración de parámetros extrínsecos, compuesto de un sistema de visión estereoscópico (1), con las cámaras izquierda (2) y derecha (3), la tarjeta de procesamiento (4) y la pantalla de visualización (5). Instalado en el parabrisas y el salpicadero de la plataforma experimental ViiA.
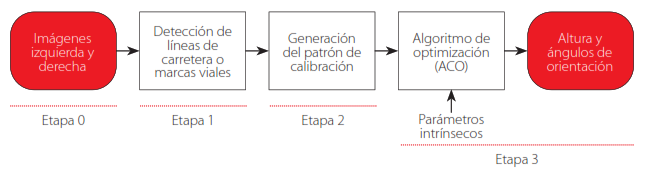
FIGURA 3.
Esquema general del algoritmo de autocalibración de extrínsecos usando optimización colonia de hormigas.
Modelo matemático de los parámetros extrínsecos
Siguiendo la metodología de Collado et al. [5] se tiene el modelo, dado por la ecuación (1) y representado en la Fig. 1(a):
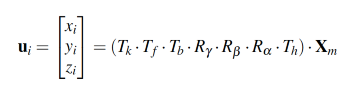 (1)
(1)donde ui representa un punto en el mundo de la cámara, Xm = (xm, ym, zm,1)T es un punto del mundo real, en este caso, extraído de las líneas de la carretera. Las matrices que forman parte de (1) son:
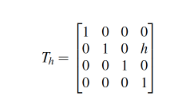 (2)
(2)
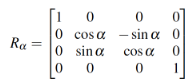 (3)
(3)
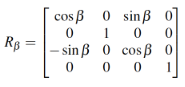 (4)
(4)
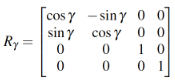 (5)
(5)
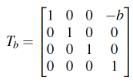 (6)
(6)
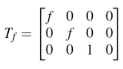 (7)
(7)
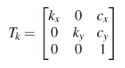 (8)
(8)Las matrices (2) a (5) permiten manejar las traslaciones y rotaciones de los sistemasde una manera eficiente, la matriz (6) relaciona las cámaras izquierda y derecha,separadas una distancia b, y las matrices (7) y (8) son los parámetros intrínsecos delas cámaras [21]. De este modo, se llega a una función multidimensional de tipo nolineal, donde intervienen los parámetros desconocidos, α (cabeceo), β (guiñada), γ(balanceo) y h (altura).
Detección de las líneas de la carretera
Para localizar y extraer los píxeles que forman las líneas de la carretera, que constituirán el patrón de calibración, se han utilizado varias técnicas sofisticadas de procesamiento de imágenes. En las imágenes de la Fig. 4 se observa el procedimiento a seguir, que consiste de cuatro pasos, (a) capturar una imagen de la escena vial, (b) filtrar con la máscara [-1,1]T , para resaltar los píxeles con alto valor del gradiente, donde los contrastes de textura entre las aristas verticales y el pavimento son más sobresalientes y que corresponden a las líneas, (c) aplicar la transformada de Hough [22], a la imagen de aristas, para estimar los parámetros (θ, p) de las rectas con mayor relevancia de la escena, (d) calcular las ecuaciones de las rectas usando (9), y finalmente, sobreponer a la imagen real.
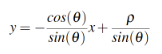 (9)
(9)ρ es una medida de distancia, en píxeles y θ está en grados.
En la práctica se ha restringido, experimentalmente, la búsqueda a un conjunto de rectas que cumplen ciertas condiciones del ángulo y la distancia, en función de la estructura vial. Esta estrategia ha sido utilizada para reducir el tiempo de cómputo y eliminar, de antemano, líneas que no corresponden a la carretera; debido a que sobre cada imagen se debe obtener únicamente dos rectas.
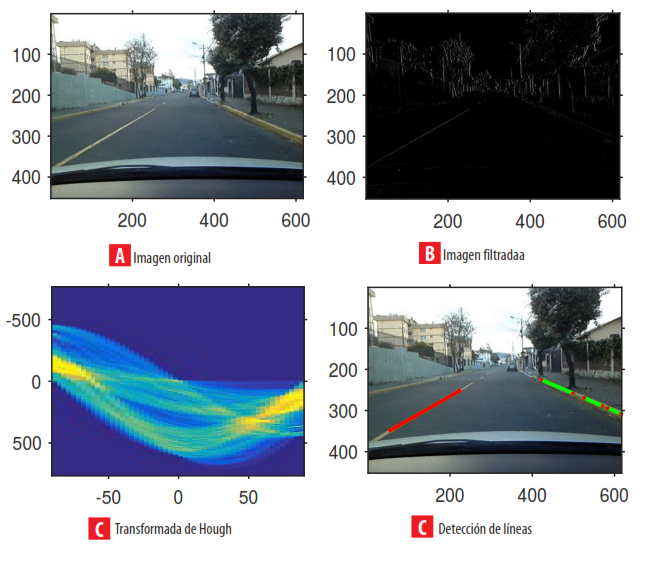
FIGURA 4.
Proceso de detección de las líneas de la carretera. (A) imagen de entrada de la escena vial, (B) gradiente vertical, (C) transformada de Hough sobre el espacio (θ, ρ), (D) superposición de las rectas sobre laslíneas de la carretera.
Estimación de los parámetros extrínsecos mediante ACO
Un algoritmo ACO es un proceso iterativo de cooperación que genera soluciones factibles a un problema de solución compleja [8]. Los principales componentes de un algoritmo ACO son los siguientes [23-25]:
-
Solución inicial: Al inicio del algoritmo, todas las feromonas tienen el valor de una constante positiva.
-
Construcción de la solución: Para construir una solución al problema de optimización, ACO maneja la aplicación de una política de decisión local estocástica rastreando información heurística y la cantidad de feromonas depositadas. Una vez que una hormiga haya construido la solución, la evalúa para que, en la etapa de actualización de feromonas, se decida cuanta cantidad de feromonas depositar.
-
Actualización de feromonas: Esta fase permite modificar la cantidad de feromonas depositadas en un camino o ruta, la cual varía conforme una hormiga deposite mayor cantidad o disminuya mediante un factor de evaporación. El que una hormiga descargue una feromona aumenta la probabilidad de que la ruta usada constituya una muy buena solución.
-
Acciones independientes: Estos procesos son usados para implementar acciones centralizadas que no pueden ser realizadas por una integrante de la ACO, por ejemplo, la aplicación de un algoritmo de diferencia evolutiva en el caso de que se haya quedado estancado.
En este caso, ACO evalúa las proyecciones del patrón obtenido desde ambas cámaras sobre el plano que forma la carretera. Así, la posición y orientación del sistema estereoscópico viene dado por diferentes hipótesis representadas por cada una de las hormigas que forman parte de la colonia artificial generada, las cuales son evaluadas hasta alcanzar una condición de fin.
Para usar ACO es necesario disponer de una función multidimensional a ser optimizada [5], dada por.
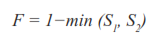 (10)
(10)La ecuación (10) tiene los siguientes componentes:
• Evalúa la coincidencia de cada punto proyectado sobre el plano de la carretera, de la cámara izquierda con la de la cámara derecha, para lo cual se utiliza como error la suma de los cuadrados de las distancias euclídeas entre las proyecciones de cada punto.
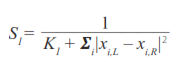 (11)
(11)con xi, Ly xi, R son el conjunto de puntos que se extraen de las rectas tomadas con las cámaras izquierda y derecha, respectivamente. K1 es una constante que se elige experimentalmente.
• Evalúa el paralelismo entre las líneas viales detectadas; dado el ángulo formado por la línea vial con el eje horizontal (n), el error determinado por el paralelismo entre las líneas vendrá dada por el mínimo entre la diferencia angular de ambas líneas tanto de la cámara izquierda y derecha.
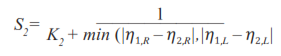 (12)
(12)K2 es una constante que se elige experimentalmente.
RESULTADOS
Parámetros del algoritmo ACO
Los parámetros necesarios para el funcionamiento del algoritmo ACO están en la Tabla 1.

Parámetros del algoritmo aco para la optimización de los parámetros extrínsecos del sistema de visión estereoscópica
El rango inicial de valores de (h, α, β, γ) tienen relación directa con la ubicación que el sistema estereoscópico debe tener al ser colocado en un vehículo, a partir de la Fig. 1(a) se espera que los dos sistemas de referencia sean paralelos entre sí, separados una distancia, comprendida entre 0,5 y 1,80 metros.
| Ancho de la imagen | 640 píxeles |
| Alto de la imagen | 480 píxeles |
| Distancia focal | 5,30 mm |
| Distancia baseline (b) | 1200,00 mm |
| Coordenada x del punto principal | 320,2604 píxeles |
| Coordenada y del punto principal | 233,6345 píxeles |
| Dimensiones de la CCD | (4,128 X 3,096) píxeles |
Parámetros intrínsecos de las cámaras izquierda y derecha y del sistema de visión estereoscópica
Parámetros intrínsecos del sistema de visión estereoscópico
La resolución de las imágenes y la distancia entre cámaras son predeterminados de antemano; mientras que la distancia focal viene dada por el fabricante. Estos valores están en las cuatro primeras filas de la Tabla 2.
A continuación, las estimaciones de los parámetros intrínsecos [21], [26] de las cámaras están en las tres últimas filas de la Tabla 2. Esta información forma parte inseparable de las matrices (7) y (8); se los estima una sola vez, en condiciones de laboratorio. Estos valores fueron obtenidos utilizado la herramienta del Caltech [27], una herramienta de libre distribución para la calibración de cámaras.
Resultados del modelo de autocalibración de parámetros extrínsecos
En los siguientes apartados se describirán los resultados más relevantes del proceso experimental de estimación.
En condiciones de laboratorio:
Para desarrollar las pruebas de funcionamiento del algoritmo en un ambiente de laboratorio, se colocaron dos líneas sobre un fondo oscuro, como se muestra en la Fig. 5.

FIGURA 5.
Imágenes tomadas en el laboratorio, donde las líneas de la carretera están completamente visibles y se conocen de antemano los parámetros a estimar. Las imágenes izquierda y derecha, corresponden a las imágenes capturadas con las cámaras izquierda y derecha, respectivamente.
Luego se preparó un conjunto de pruebas con distintas variaciones de la posición del sistema de visión estereoscópica, para así validar el modelo propuesto. La Fig. 6 muestra los distintos casos que se pueden suscitar; de todos ellos, el caso (a) es el ideal, porque no existe desplazamiento de los ángulos. El resto de las situaciones son habituales debido a que es extremadamente difícil ubicar el sistema en la posición correcta; de allí, la necesidad de la calibración.
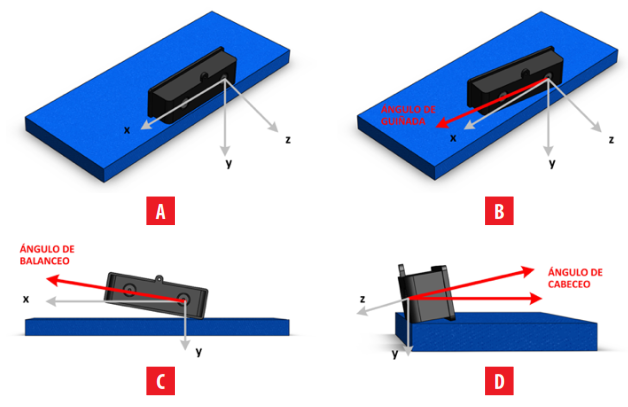
FIGURA 6.
Posiciones del sistema de visión estereoscópico para desarrollar los experimentos de estimación de los parámetros extrínsecos en el laboratorio. El origen se encuentra en la cámara izquierda. A) posición ideal, B) 5 grados en la guiñada, C) 2 grados en el balanceo y D) 2 grados en el cabeceo.
Las Tablas 3, 4, 5, 6 muestran los resultados obtenidos dadas las diferentes variaciones de la posición del sistema según la Fig. 6, en los casos (a), (b), (c) y (d) respectivamente, así como la varianza y el error porcentual de los parámetros estimados comparados con los '"gemems parámetros reales. Estos valores se obtuvieron realizando diez ejecuciones del algoritmo en cada caso.
| Parámetro | Altura | Distancia entre líneas | Cabeceo | Guiñada | Balanceo | |||
| [mm] | [mm] | [rad] | [°] | [rad] | [°] | [rad] | [°] | |
| Real | 760,00 | 2800,00 | 0,01745 | 0,9999 | -0,01745 | -0,9999 | 0,01745 | 0,9999 |
| Calculado | 738,788 | 2560,00 | 0,01641 | 0,94028 | -0,02752 | 1,57712 | 0,02160 | 1,23808 |
| Varianza | 21,212 | 240,00 | 0,00104 | 0,05962 | 0,01001 | 0,05772 | -0,00416 | -0,23819 |
| Error porcentual | 2,8% | 8,6% | 6,0% | 6,0% | 57,7% | 57,7% | -23,8% | -23,8% |
Resultados del algoritmo aco, en ambiente de laboratorio, a una altura de 760,00 mm
| Parámetro | Altura | Distancia entre líneas | Cabeceo | Guiñada | Balanceo | |||
| [mm] | [mm] | [rad] | [°] | [rad] | [°] | [rad] | [°] | |
| Real | 760,00 | 2800,00 | 0,01745 | 0,9999 | 0,0872 | 5,0000 | 0,01745 | 0,9999 |
| Calculado | 738,898 | 2561,00 | 0,01599 | 0,91662 | 0,07470 | 4,27999 | 0,02131 | 1,22097 |
| Varianza | 21,102 | 239,00 | 0,00145 | 0,08328 | 0,01250 | 0,72000 | -0,00386 | -0,22107 |
| Error porcentual | 2,8% | 8,5% | 8,3% | 8,3% | 14,3% | 14,4% | -22,1% | -22,1% |
Resultados del algoritmo aco, en ambiente de laboratorio, con variación del ángulo de guiñada
En condiciones de reales:
En esta etapa se realizaron pruebas de funcionamiento del algoritmo en un ambiente real de carretera, en este caso es importante tener en cuenta que es necesario contar con marcas viales claramente visibles y marcadas como
| Parámetro | Altura | Distancia entre líneas | Cabeceo | Guiñada | Balanceo | |||
| [mm] | [mm] | [rad] | [°] | [rad] | [°] | [rad] | [°] | |
| Real | 760,00 | 2800,00 | 0,01745 | 0,9999 | 0,01745 | 0,9999 | 0,03491 | 2,0000 |
| Calculado | 745,258 | 2560,00 | 0,01850 | 1,05997 | 0,01364 | 0,78151 | 0,02022 | 1,15852 |
| Varianza | 14,742 | 240,00 | -0,00105 | -0,06007 | 0,00381 | 0,21838 | 0,01469 | 0,84148 |
| Error relativo | 1,9% | 8,6% | -6,0% | -6,0% | 21,8% | 21,8% | 42,1% | 42,1% |
Resultados del algoritmo aco, en ambiente de laboratorio, con variación del ángulo de balanceo
| Parámetro | Altura | Distancia entre líneas | Cabeceo | Guiñada | Balanceo | |||
| [mm] | [mm] | [rad] | [°] | [rad] | [°] | [rad] | [°] | |
| Real | 760,00 | 2800,00 | 0,03491 | 2,0000 | 0,01745 | 0,9999 | 0,01745 | 0,9999 |
| Calculado | 744,540 | 2562,00 | 0,02826 | 1,61918 | 0,02121 | 1,21524 | 0,02133 | 1,22211 |
| Varianza | 15,460 | 238,00 | 0,00665 | 0,03882 | -0,00376 | -0,21534 | -0,00388 | -0,22224 |
| Error relativo | 2,0% | 8,5% | 19,0% | 19,0% | -21,5% | -21,5% | -22,2% | -22,2% |
Resultados del algoritmo aco, en ambiente de laboratorio, con variación del ángulo de cabeceo
se muestra en la Fig. 7. Los resultados de este caso se encuentran en la Tabla 7, en esta fase no se conoce a priori la información de los parámetros extrínsecos.

FIGURA 7.
Imágenes tomadas en un ambiente de carretera real. Las líneas de la carretera están visibles, sobre las imágenes izquierda y derecha, respectivamente.
| Parámetro | Altura | Distancia entre líneas | Cabeceo | Guiñada | Balanceo | |||
| [mm] | [mm] | [rad] | [°] | [rad] | [°] | [rad] | [°] | |
| Real | 1250,00 | 3000,00 | 0,13962 | 8,00 | 0,0349 | 2,00 | -0,0349 | -2,00 |
| Calculado | 1132,52 | 2751,00 | 0,13901 | 7,9646 | 0,0213 | 1,223 | -0,02795 | -1,6014 |
| Varianza | 117,48 | 249,00 | 0,00061 | 0,0354 | 0,00136 | 0,777 | 0,00695 | 0,3986 |
| Error relativo | 9,3% | 8,3% | 0,4% | 0,4% | 39,0% | 39,0% | 20,0% | 19,9% |
Resultados del algoritmo aco, en ambiente de laboratorio, a una altura de 1250,00 mm
Comparación entre ACO y AG:
A continuación, el algoritmo ACO fue comparado con los resultados expuestos en Collado et al. [5], el cual utiliza un algoritmo genético (AG) para resolver el problema de minimización. En la Tabla 8 se muestran los resultados generados con los dos métodos.
En ambos casos se tienen resultados aceptables, sin embargo AG presenta menores errores, pero no tiene resultados de los ángulos de guiñada y balanceo.
| Parámetro | Altura | Cabeceo | Guiñada | Balanceo | |||
| [mm] | [rad] | [°] | [rad] | [°] | [rad] | [°] | |
| Real | 1500,00 | 0,1700 | 9,74 | No hay datos | No hay datos | -0,0900 | -5,15 |
| Calculado AG | 1458,0 | 0,1691 | 9,69 | - | - | -0,0933 | -5,35 |
| Calculado ACO | 1461,39 | 0,1551 | 8,8866 | -0,01707 | -0,0978 | -0,09431 | -5,4035 |
| Error relativo AG | 2,8% | 0,5% | 0,5% | - | - | -3,3% | -3,8% |
| Error relativo ACO | 2,6% | 8,8% | 8,8% | - | - | -4,8% | -4,9% |
Comparación de los resultados del algoritmo aco versus el algoritmo AG [5]
Tiempo de procesamiento
El tiempo de procesamiento no es un impedimento en este tipo de sistemas, debido a que la autocalibración se la realiza una sola vez, en condiciones de reposo. Aun así, se indica que el tiempo de procesamiento fue de 24 milisegundos, sobre un PC Core I7 de 64 bits, con 7.7 GB de memoria RAM.
CONCLUSIONES Y TRABAJOS FUTUROS
Este trabajo de investigación es un paso importante en el desarrollo de sistemas inteligentes, basados en visión por computador, destinados a los vehículos autónomos y vehículos inteligentes. Tanto es así que se realizaron los siguientes aportes:
-
El desarrollo de un nuevo algoritmo para estimar los tres ángulos de orientación y la altura, mediante la técnica de optimización colonia de hormigas y la infraestructura vial (líneas de la carretera), para relacionar eficientemente los sistemas de referencia del mundo y la cámara.
-
Este algoritmo genera un error global del 8% en condiciones de laboratorio y del 9% en condiciones reales sobre la infraestructura vial. Esta implementación es muy competitiva, en la fase de optimización de la función objetivo, al ser comparada con otras propuestas.
A futuro se extenderá esta metodología para el caso de la autocalibración dinámica, para ser utilizada en aplicaciones de navegación autónoma, con autocalibración en ambientes no controlados y en tiempo real.
FUENTES DE FINANCIAMIENTO
Este proyecto ha recibido financiamiento indirecto, a través del préstamo de los equipos informáticos, el sistema de visión estereoscópico y el vehículo ViiA, de la empresa Tecnologías I&H.
APORTE DEL ARTÍCULO EN LA LÍNEA DE INVESTIGACIÓN
El presente artículo es un aporte en la línea de investigación de procesamiento digital de señales, en el área de visión por computador. En particular, el tema de autocalibración de los parámetros extrínsecos de un sistema de visión estereoscópico usando la infraestructura vial de las líneas de la carretera sin intervención humana, es importante para el desarrollo de tecnología destinada a los vehículos autónomos.
DECLARACIÓN DE CONTRIBUCIÓN DE CADA AUTOR
El diseño de la investigación, el desarrollo y la implementación de parte del software, la supervisión y el análisis de los resultados experimentales corresponden a M. Flores. Parte de la implementación del software y el desarrollo de los experimentos pertenecen a E. Arévalo. La redacción y la preparación del texto recaen en M. Aldás, y la revisión final es de M. Gualsaquí.
AGRADECIMIENTOS
Para el desarrollo de una parte significativa de este proyecto se ha contado con el apoyo de la empresa Tecnologías I&H, a ella nuestro agradecimiento. Además, agradecemos a los revisores anónimos por su valioso aporte ya que han contribuido significativamente en el perfeccionamiento de este documento.
REFERENCIAS
[1] Riccardo Turchetto and Roberto Manduchi. Visual curb localization for autonomous navigation. 2:1336-1342, 2003. doi: https://dx.doi.org/10.1109/IROS.2003.1248830
[2] Stefan Ernst, Christop Stiller, Jens Goldbeck, and Christoph Roessig. Camera calibration for lane and obstacle detection. pages 356 - 361, 1999.
[3] A Broggi, M. Bertozzi, and A. Fascioli. Self-calibration of a stereo vision system for automotive applications. 4:36983703, 2001. doi: https://dx.doi.org/10.1109/ROBOT.2001.933193
[4] Adnan Shaout, Dominic Colella, and S. Awad. Advanced driver assistance systems past, present, and future. IEEE International Computer Engineering Conference (ICENCO), February 2012. doi: https://dx.doi.org/10.1109/ICENCO.2011.6153935
[5] Juan M Collado, Cristina Hilario, Arturo de la Escalera, and Jose M Armingol. Self-calibration of an on-board stereovision system for driver assistance systems. In Intelligent Vehicles Symposium, 2006 IEEE, pages 156 - 162. IEEE, 2006. doi: https://doi.org/10.1016/j.robot.2007.09.004
[6] Angel Sappa, David Gerónimo, Fadi Dornaika, and Antonio López. Real time vehicle poses using on-board stereo vision system. pages 205-216, 2006. doi: https://doi.org/10.1007/11867661_19
[7] Marco Dorigo, Vittorio Maniezzo, and Alberto Colorni. Ant system: optimization by a colony of cooperating agents. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 26(1):29-41, 1996. Doi: https://dx.doi.org/10.1109/3477.484436
[8] Christian Blum and Andrea Roli. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv., 35(3):268-308, 2003. doi: https://doi.org/10.1145/937503.937505
[9] Marco Dorigo and Luca Maria Gambardella. Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Transactions on evolutionary computation, 1(1):53-66, 1997. doi: https://dx.doi.org/10.1109/4235.585892
[10] Fenglei Du and Michael Brady. Self-calibration of the intrinsic parameters of cameras for active vision systems. In Computer Vision and Pattern Recognition, 1993. Proceedings CVPR’93., 1993 IEEE Computer Society Conference on, pages 477-482. IEEE, 1993. doi: https://dx.doi.org/10.1109/CVPR.1993.341087
[11] Manuel Ortega Cantero. Informática Industrial. Ediciones Univesidad Castilla - La Mancha, 1997.
[12] Zhengyou Zhang. A flexible new technique for camera calibration. IEEE Transactions on pattern analysis and machine intelligence, 22(11):1330-1334, 2000. doi: https://dx.doi.org/10.1109/34.888718
[13] Roger Tsai. A versatile camera calibration technique for high accuracy 3d machine vision metrology using off-the- shelf tv cameras and lenses. IEEE Journal on Robotics and Automation, 3(4):323-344, 1987. doi: https://dx.doi.org/10.1109/JRA.1987.1087109
[14] Juan Manuel Collado Hernaiz. Detección y Modelado de Carriles de Vías Interurbanas mediante Análisis de Imágenes para un Sistema de Ayuda a la Conducción. Tesis doctoral, Universidad Carlos III de Madrid, 2009. Directores: A. de la Escalera, J. Armingol.
[15] Theo Dang and Christian Hoffmann. Stereo calibration in vehicles. In Intelligent Vehicles Symposium, 2004 IEEE, pages 268-273. IEEE, 2004. doi: https://dx.doi.org/10.1109/IVS.2004.1336393
[16] Qi Wang, Qin Zhang, and Francisco Rovira-Más. Auto-calibration method to determine camera pose for stereovision based off-road vehicle navigation. Environment Control in Biology, 48(2):59-72, 2010. doi: https://doi.org/10.2525/ecb.48.59
[17] Richard Hartley and Andrew Zisserman. Multiple View Geometry in Computer Vision (2nd edition). Cambridge University Press, 2003.
[18] Basam Musleh, David Martín, José María Armingol, and Arturo de la Escalera. Extrinsic parameter self-calibration and nonlinear filtering for in-vehicle stereo vision systems at urban environments. In Computer Vision Theory and Applications (VISAPP), 2014 International Conference on, volume 3, pages 427-434. IEEE, 2014.
[19] Robert Spangenberg, Tobias Langner, and Raúl Rojas. On-line stereo self-calibration through minimization of matching costs. In Scandinavian Conference on Image Analysis, pages 545-554. Springer, 2013. doi: https://doi.org/10.1007/978-3-642-38886-6_51
[20] Mauricio Braga de Paula, Cláudio Rosito Jung, and LG Da Silveira. Automatic on-the-fly extrinsic camera calibration of onboard vehicular cameras. Expert Systems with Applications, 41(4):1997-2007, 2014. doi: https://doi.org/10.1016/j.eswa.2013.08.096
[21] Olivier Faugeras. Three-dimensional computer vision: a geometric viewpoint. MIT press, 1993.
[22] R. O. Duda and P. E. Hart. Use of the hough transformation to detect lines and curves in pictures. In Comm. ACM, volume 13, pages 111-122, 1981.
[23] Marco Dorigo. Optimization, learning and natural algorithms. Ph. D. Thesis, Politecnico di Milano, Italy, 1992.
[24] Marco Dorigo, Mauro Birattari, and Thomas Stützle. Ant colony optimization. IEEE computational intelligence jornal, 1(4):28-39, 2006. doi: https://dx.doi.org/10.1109/MCI.2006.329691
[25] Dorigo, M., & Blum, C. (2005). Ant colony optimization theory: A survey. Theoretical computer science, 344(2-3), 243-278. doi: https://doi.org/10.1016/j.tcs.2005.05.020
[26] Alejandro Barranco, Saúl Martínez, and José Luis Gómez. Visión estereoscópica por computadora con Matlab y OpenCV. Editorial Lulu, jun 2012.
[27] Jean-Yves Bouguet. Camera calibration toolbox for matlab, 2006.